沪科新版 八年级数学上册 第12章 一次函数 单元测试卷 (Word版 含解析)
文档属性
| 名称 | 沪科新版 八年级数学上册 第12章 一次函数 单元测试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 06:52:11 | ||
图片预览




文档简介
第12章 一次函数 单元测试卷
一、选择题(共10小题).
1.函数y=中自变量x的取值范围是( )
A.x≠﹣4 B.x≠4 C.x≤﹣4 D.x≤4
2.下列四个点中,恰好与点(﹣2,4)在同一个正比例函数图象上的是( )
A.(4,﹣2) B.(2,﹣4) C.(﹣4,2) D.(2,4)
3.在下列各图象中,y是x的函数有( )
A.1个 B.2个 C.3个 D.4个
4.若点A(x1,﹣3),B(x2,﹣2),C(x3,1)在一次函数y=3x﹣b的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x1<x3 C.x3<x2<x1 D.x1<x3<x2
5.在平面直角坐标系中,若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度后恰好经过点(﹣1,﹣2),则n的值为( )
A.10 B.8 C.5 D.3
6.将直线y=2x+1向右平移2个单位.再向上平移2个单位后,得到直线y=kx+b.则下列关于直线y=kx+b的说法正确的是( )
A.与x轴交于(2,0) B.与y轴交于(0,﹣1)
C.y随x的增大而减小 D.经过第一、二、四象限
7.已知y是x的一次函数,下表中列出了部分对应值,则m等于( )
x ﹣1 0 1
y 1 m ﹣5
A.﹣1 B.0 C.﹣2 D.
8.若点A(﹣2,a),B(b,)在同一个正比例函数图象上,则的值是( )
A. B.﹣3 C.3 D.﹣
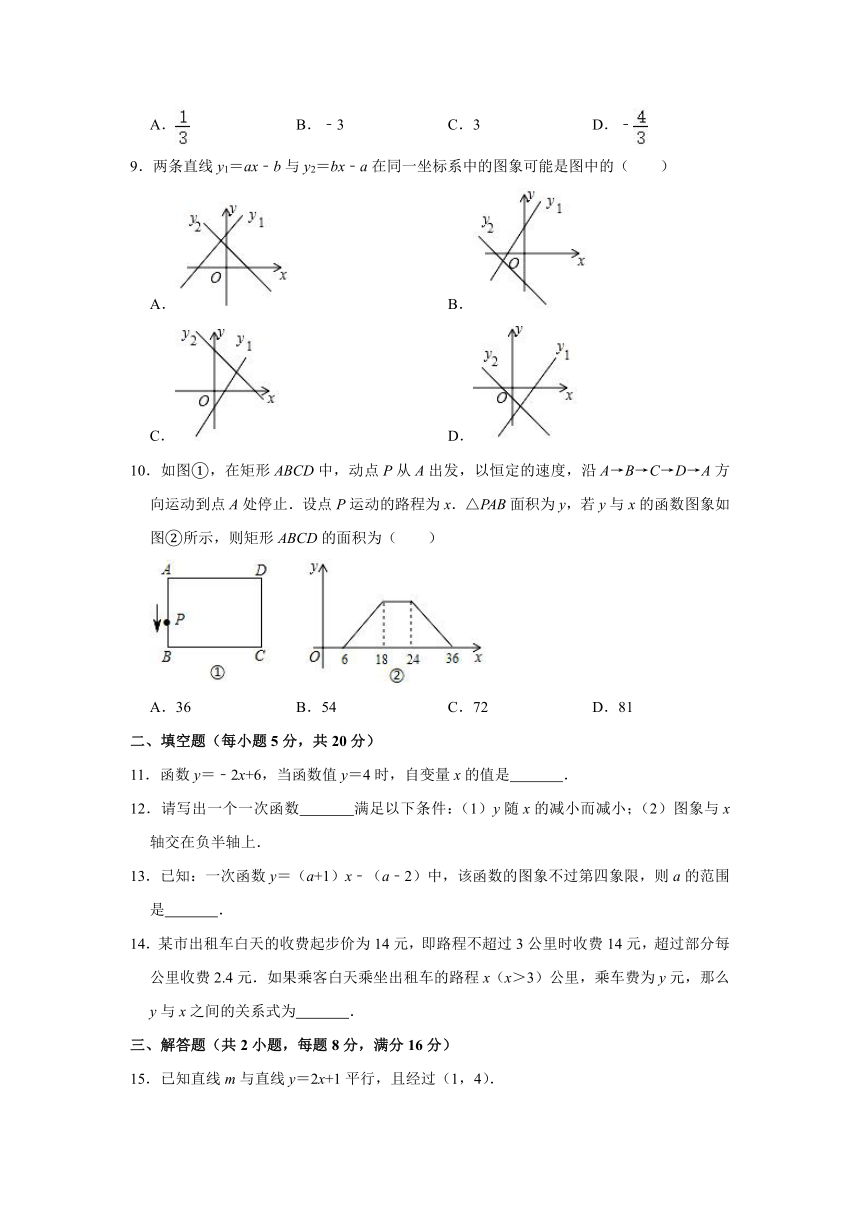
9.两条直线y1=ax﹣b与y2=bx﹣a在同一坐标系中的图象可能是图中的( )
A. B.
C. D.
10.如图①,在矩形ABCD中,动点P从A出发,以恒定的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x.△PAB面积为y,若y与x的函数图象如图②所示,则矩形ABCD的面积为( )
A.36 B.54 C.72 D.81
二、填空题(每小题5分,共20分)
11.函数y=﹣2x+6,当函数值y=4时,自变量x的值是 .
12.请写出一个一次函数 满足以下条件:(1)y随x的减小而减小;(2)图象与x轴交在负半轴上.
13.已知:一次函数y=(a+1)x﹣(a﹣2)中,该函数的图象不过第四象限,则a的范围是 .
14.某市出租车白天的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客白天乘坐出租车的路程x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 .
三、解答题(共2小题,每题8分,满分16分)
15.已知直线m与直线y=2x+1平行,且经过(1,4).
(1)求直线m的解析式.
(2)求直线m与x轴的交点.
16.已知y﹣2与x+3成正比例,且x=﹣4时,y=0.
(1)求y与x之间的函数关系式;
(2)点P1(2m﹣2,2m+1)在(1)中所得函数的图象上,求m的值.
四、解答题(本答题共两小题,每题8分,满分16分)
17.某汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.
(1)求y与x之间的函数关系.
(2)旅客最多可以免费携带多少千克的行李?
18.某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
五、解答题(本答题共两小题,每题10分,满分20分)
19.已知点A(4,0)及在第一象限的动点P(x,y),且x+y=10,O为坐标原点,设△OPA的面积为S.
(1)求S关于x的函数解析式;
(2)当S=4时,求P点的坐标.
20.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx+2(m+1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为3,求m值.
六、解答题(本题满分12分)
21.如图,在平面直角坐标系中,直线y=﹣x+3过点A(5,m)且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C.过点C且与y=2x平行的直线交y轴于点D.
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
七、解答题(本题满分12分)
22.预防新型冠状病毒期间,某种消毒液甲城需要7吨,乙城需要8吨,正好A地储备有10吨,B地储备有5吨,市预防新型冠状病毒领导小组决定将A、B两地储备的这15吨消毒液全部调往甲城和乙城,消毒液的运费价格如下表(单位:元/吨),设从A地调运x吨消毒液给甲城.
终点 起点 甲城 乙城
A地 100 120
B地 110 95
(1)根据题意,应从B地调运 吨消毒液给甲城,从B地调运 吨消毒液给乙城;(结果请用含x的代数式表示)
(2)求调运这15吨消毒液的总运费y关于x的函数关系式,并直接写出x的取值范围;
(3)求出总运费最低的调运方案,并算出最低运费.
八、解答题(本题满分14分)
23.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300km.
参考答案
一、选择题(共10小题).
1.函数y=中自变量x的取值范围是( )
A.x≠﹣4 B.x≠4 C.x≤﹣4 D.x≤4
解:由题意得,4﹣x≠0,
解得x≠4.
故选:B.
2.下列四个点中,恰好与点(﹣2,4)在同一个正比例函数图象上的是( )
A.(4,﹣2) B.(2,﹣4) C.(﹣4,2) D.(2,4)
解:设正比例函数的解析式为:y=kx,
把(﹣2,4)代入得:
4=﹣2k,
解得:k=﹣2,
即正比例函数的解析式为:y=﹣2x,
A.把x=4代入y=﹣2x得:y=﹣8,即A项错误,
B.把x=2代入y=﹣2x得:y=﹣4,即B项正确,
C.把x=﹣4代入y=﹣2x得:y=8,即C项错误,
D.把x=2代入y=﹣2x得:y=﹣4,即D项错误,
故选:B.
3.在下列各图象中,y是x的函数有( )
A.1个 B.2个 C.3个 D.4个
解:第一个、第二个、第三个图象y都是x的函数,第四个不是,共3个,
故选:C.
4.若点A(x1,﹣3),B(x2,﹣2),C(x3,1)在一次函数y=3x﹣b的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x1<x3 C.x3<x2<x1 D.x1<x3<x2
解:∵一次函数y=3x﹣b中,k=3>0,
∴y随x的增大而增大;
∵点A(x1,﹣3),B(x2,﹣2),C(x3,1),
∴x1<x2<x3;
故选:A.
5.在平面直角坐标系中,若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度后恰好经过点(﹣1,﹣2),则n的值为( )
A.10 B.8 C.5 D.3
解:∵若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度,
∴平移后的函数解析式为:y=﹣2x+6﹣n,
∵函数解y=﹣2x+6﹣n的图象经过点(﹣1,﹣2),
∴﹣2=﹣2×(﹣1)+6﹣n,
解得:n=10,
故选:A.
6.将直线y=2x+1向右平移2个单位.再向上平移2个单位后,得到直线y=kx+b.则下列关于直线y=kx+b的说法正确的是( )
A.与x轴交于(2,0) B.与y轴交于(0,﹣1)
C.y随x的增大而减小 D.经过第一、二、四象限
解:将直线y=2x+1向右平移2个单位.再向上平移2个单位后得到直线y=2x﹣1,
A、直线y=2x﹣1与x轴交于(2,0),错误;
B、直线y=2x﹣1与y轴交于(0,﹣1),正确
C、直线y=2x﹣1,y随x的增大而增大,错误;
D、直线y=2x﹣1经过第一、三、四象限,错误;
故选:B.
7.已知y是x的一次函数,下表中列出了部分对应值,则m等于( )
x ﹣1 0 1
y 1 m ﹣5
A.﹣1 B.0 C.﹣2 D.
解:设一次函数解析式为y=kx+b,
将x=﹣1,y=1;x=1,y=﹣5代入得:,
解得:k=﹣3,b=﹣2,
∴一次函数解析式为y=﹣3x﹣2,
令x=0,得到y=2,
则m=﹣2,
故选:C.
8.若点A(﹣2,a),B(b,)在同一个正比例函数图象上,则的值是( )
A. B.﹣3 C.3 D.﹣
解:设正比例函数解析式为y=kx,
∵点A(﹣2,a),B(b,)都在该函数图象上,
∴a=﹣2k,bk=,
即k=a,
∴,
∴ab=﹣3,
∴原式==,
故选:A.
9.两条直线y1=ax﹣b与y2=bx﹣a在同一坐标系中的图象可能是图中的( )
A. B.
C. D.
解:A:直线y1过第一、二、三象限,则a>0,b<0,直线y2过第一、二、四象限,则b<0,a<0,前后矛盾,故A选项错误;
B:直线y1过第一、二、三象限,则a>0,b<0,直线y2过第二、三、四象限,则b<0,a>0,故B选项正确;
C:直线y1过第一、三、四象限,则a>0,b>0,直线y2过第一、二、四象限,则b<0,a<0,前后矛盾,故C选项错误;
D:直线y1过第一、三、四象限,则a>0,b>0,直线y2过第二、三、四象限,则b<0,a>0,前后矛盾,故D选项错误;
故选:B.
10.如图①,在矩形ABCD中,动点P从A出发,以恒定的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x.△PAB面积为y,若y与x的函数图象如图②所示,则矩形ABCD的面积为( )
A.36 B.54 C.72 D.81
解:由题意及图②可知:
AB=6,BC=18﹣6=12,
∴矩形ABCD的面积为6×12=72.
故选:C.
二、填空题(每小题5分,共20分)
11.函数y=﹣2x+6,当函数值y=4时,自变量x的值是 1 .
解:当y=4时,﹣2x+6=4,
解得:x=1.
故答案为:1.
12.请写出一个一次函数 y=x+1 满足以下条件:(1)y随x的减小而减小;(2)图象与x轴交在负半轴上.
解:y=x+1满足条件y随x的减小而减小,图象与x轴交在负半轴上,
故答案为:y=x+1.
13.已知:一次函数y=(a+1)x﹣(a﹣2)中,该函数的图象不过第四象限,则a的范围是 ﹣1<a≤2 .
解:∵一次函数y=(a+1)x﹣(a﹣2)的图象不过第四象限,
∴,
解得﹣1<a≤2.
故答案为﹣1<a≤2.
14.某市出租车白天的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客白天乘坐出租车的路程x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 y=2.4x+6.8 .
解:依题意有:y=14+2.4(x﹣3)=2.4x+6.8.
故答案为:y=2.4x+6.8.
三、解答题(本答题共两小题,每题8分,满分16分)
15.已知直线m与直线y=2x+1平行,且经过(1,4).
(1)求直线m的解析式.
(2)求直线m与x轴的交点.
解:(1)设直线m为y=kx+b,
∵直线m与直线y=2x+1平行,
∴k=2,
把(1,4)代入y=2x+b得:b=2,
∴直线m的解析式为:y=2x+2;
(2)在直线m:y=2x+2中,令y=0,则2x+2=0,
解得x=﹣1,
∴直线m与x轴的交点为(﹣1,0).
16.已知y﹣2与x+3成正比例,且x=﹣4时,y=0.
(1)求y与x之间的函数关系式;
(2)点P1(2m﹣2,2m+1)在(1)中所得函数的图象上,求m的值.
解:(1)设y﹣2=k(x+3)(k≠0),
把x=﹣4,y=0代入得,0﹣2=k(﹣4+3),
解得,k=2,
∴y﹣2=2(x+3),
即:y=2x+8,
(2)∵点P1(2m﹣2,2m+1)在y=2x+8的图象上,
∴2m+1=2(2m﹣2)+8,
∴m=﹣,
四、解答题(本答题共两小题,每题8分,满分16分)
17.某汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.
(1)求y与x之间的函数关系.
(2)旅客最多可以免费携带多少千克的行李?
解:(1)设一次函数y=kx+b,
∵当x=60时,y=6,当x=90时,y=10,
∴ 解之,得,
∴所求函数关系式为y=x﹣2(x≥15);
(2)当y=0时,x﹣2=0,所以x=15,
故旅客最多可免费携带15kg行李.
18.某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
解:(1)设y甲=k1x,根据题意得5k1=100,解得k1=20,∴y甲=20x;
设y乙=k2x+100,根据题意得:20k2+100=300,解得k2=10,∴y乙=10x+100;
(2)①y甲<y乙,即20x<10x+100,解得x<10,当入园次数小于10次时,选择甲消费卡比较合算;
②y甲=y乙,即20x=10x+100,解得x=10,当入园次数等于10次时,选择两种消费卡费用一样;
③y甲>y乙,即20x>10x+100,解得x>10,当入园次数大于10次时,选择乙消费卡比较合算.
五、解答题(本答题共两小题,每题10分,满分20分)
19.已知点A(4,0)及在第一象限的动点P(x,y),且x+y=10,O为坐标原点,设△OPA的面积为S.
(1)求S关于x的函数解析式;
(2)当S=4时,求P点的坐标.
解:(1)如图所示,
∵x+y=10,
∴y=10﹣x,
∴S=×4×(10﹣x)=20﹣2x;
(2)由(1)知,S=20﹣2x,
∴20﹣2x=4,解得x=8,
∴y=2,
∴P(8,2).
20.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx+2(m+1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为3,求m值.
解:(1)当x≥0时,y=|x|=x,即y=x(x≥0),
将x=0代入得:y=0;
将x=1代入得:y=1,
当x≤0时,y=|x|=﹣x,即y=﹣x(x≤0),
将x=0代入得:y=0;
将x=﹣1代入得:y=1.
过点O(0,0),A(﹣1,1)作射线OA,过点O(0,0),B(1,1)作射线OB,
函数y=|x|的图象如图所示:
(2)∵y=mx+2(m+1)=m(x+2)+2,
∴x+2=0,y=2
∴x=﹣2,y=2,
即无论m取何值,函数y=mx+2(m+1)的图象经过的一个确定的点(﹣2,2);
(3)如下图:
∵函数y=mx+2(m+1)的图象经过顶点(﹣2,2)
∴OC==2.
∴OD?OC=3,
∴OD=,
所以点D的坐标为(,).
将x=,y=代入y=mx+2(m+1)得:m=﹣.
六、解答题(本题满分12分)
21.如图,在平面直角坐标系中,直线y=﹣x+3过点A(5,m)且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C.过点C且与y=2x平行的直线交y轴于点D.
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
解:(1)把A(5,m)代入y=﹣x+3得m=﹣5+3=﹣2,则A(5,﹣2),
∵点A向左平移2个单位,再向上平移4个单位,得到点C,
∴C(3,2),
∵过点C且与y=2x平行的直线交y轴于点D,
∴CD的解析式可设为y=2x+b,
把C(3,2)代入得6+b=2,解得b=﹣4,
∴直线CD的解析式为y=2x﹣4;
(2)当x=0时,y=﹣x+3=3,则B(0,3),
当y=0时,2x﹣4=0,解得x=2,则直线CD与x轴的交点坐标为(2,0);
易得CD平移到经过点B时的直线解析式为y=2x+3,
当y=0时,2x+3=0,解得x=﹣,则直线y=2x+3与x轴的交点坐标为(﹣,0),
∴直线CD在平移过程中与x轴交点的横坐标的取值范围为﹣≤x≤2.
七、解答题(本题满分12分)
22.预防新型冠状病毒期间,某种消毒液甲城需要7吨,乙城需要8吨,正好A地储备有10吨,B地储备有5吨,市预防新型冠状病毒领导小组决定将A、B两地储备的这15吨消毒液全部调往甲城和乙城,消毒液的运费价格如下表(单位:元/吨),设从A地调运x吨消毒液给甲城.
终点 起点 甲城 乙城
A地 100 120
B地 110 95
(1)根据题意,应从B地调运 (7﹣x) 吨消毒液给甲城,从B地调运 (x﹣2) 吨消毒液给乙城;(结果请用含x的代数式表示)
(2)求调运这15吨消毒液的总运费y关于x的函数关系式,并直接写出x的取值范围;
(3)求出总运费最低的调运方案,并算出最低运费.
解:(1)由题意可得,
从A地调运x吨消毒液给甲城,则调运(10﹣x)吨消毒液给乙城,从B地调运(7﹣x)吨消毒液给甲城,调运8﹣(10﹣x)=(x﹣2)吨消毒液给乙城,
故答案为:(7﹣x),(x﹣2);
(2)由题意可得,
y=100x+120(10﹣x)+110(7﹣x)+95(x﹣2)=﹣35x+1780,
∵,
∴2≤x≤7,
即总运费y关于x的函数关系式是y=﹣35x+1780(2≤x≤7);
(3)∵y=﹣35x+1780,
∴y随x的增大而减小,
∵2≤x≤7,
∴当x=7时,y取得最小值,此时y=1535,
即从A地调运7吨消毒液给甲城时,总运费最低,运费最低为1535元.
八、解答题(本题满分14分)
23.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)慢车的速度为 80 km/h,快车的速度为 120 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300km.
解:(1)(480﹣440)÷0.5=80km/h,
440÷(2.7﹣0.5)﹣80=120km/h,
所以,慢车速度为80km/h,
快车速度为120km/h;
故答案为:80;120.
(2)快车到达乙地(出发了4小时快车慢车相距360KM时甲车到达乙地);
∵快车走完全程所需时间为480÷120=4(h),
∴点D的横坐标为4.5,
纵坐标为(80+120)×(4.5﹣2.7)=360,
即点D(4.5,360);
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为300km.
即相遇前:(80+120)×(x﹣0.5)=440﹣300,
解得x=1.2(h),
相遇后:(80+120)×(x﹣2.7)=300,
解得x=4.2(h),
故x=1.2 h或4.2 h,两车之间的距离为300km.
一、选择题(共10小题).
1.函数y=中自变量x的取值范围是( )
A.x≠﹣4 B.x≠4 C.x≤﹣4 D.x≤4
2.下列四个点中,恰好与点(﹣2,4)在同一个正比例函数图象上的是( )
A.(4,﹣2) B.(2,﹣4) C.(﹣4,2) D.(2,4)
3.在下列各图象中,y是x的函数有( )
A.1个 B.2个 C.3个 D.4个
4.若点A(x1,﹣3),B(x2,﹣2),C(x3,1)在一次函数y=3x﹣b的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x1<x3 C.x3<x2<x1 D.x1<x3<x2
5.在平面直角坐标系中,若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度后恰好经过点(﹣1,﹣2),则n的值为( )
A.10 B.8 C.5 D.3
6.将直线y=2x+1向右平移2个单位.再向上平移2个单位后,得到直线y=kx+b.则下列关于直线y=kx+b的说法正确的是( )
A.与x轴交于(2,0) B.与y轴交于(0,﹣1)
C.y随x的增大而减小 D.经过第一、二、四象限
7.已知y是x的一次函数,下表中列出了部分对应值,则m等于( )
x ﹣1 0 1
y 1 m ﹣5
A.﹣1 B.0 C.﹣2 D.
8.若点A(﹣2,a),B(b,)在同一个正比例函数图象上,则的值是( )
A. B.﹣3 C.3 D.﹣
9.两条直线y1=ax﹣b与y2=bx﹣a在同一坐标系中的图象可能是图中的( )
A. B.
C. D.
10.如图①,在矩形ABCD中,动点P从A出发,以恒定的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x.△PAB面积为y,若y与x的函数图象如图②所示,则矩形ABCD的面积为( )
A.36 B.54 C.72 D.81
二、填空题(每小题5分,共20分)
11.函数y=﹣2x+6,当函数值y=4时,自变量x的值是 .
12.请写出一个一次函数 满足以下条件:(1)y随x的减小而减小;(2)图象与x轴交在负半轴上.
13.已知:一次函数y=(a+1)x﹣(a﹣2)中,该函数的图象不过第四象限,则a的范围是 .
14.某市出租车白天的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客白天乘坐出租车的路程x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 .
三、解答题(共2小题,每题8分,满分16分)
15.已知直线m与直线y=2x+1平行,且经过(1,4).
(1)求直线m的解析式.
(2)求直线m与x轴的交点.
16.已知y﹣2与x+3成正比例,且x=﹣4时,y=0.
(1)求y与x之间的函数关系式;
(2)点P1(2m﹣2,2m+1)在(1)中所得函数的图象上,求m的值.
四、解答题(本答题共两小题,每题8分,满分16分)
17.某汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.
(1)求y与x之间的函数关系.
(2)旅客最多可以免费携带多少千克的行李?
18.某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
五、解答题(本答题共两小题,每题10分,满分20分)
19.已知点A(4,0)及在第一象限的动点P(x,y),且x+y=10,O为坐标原点,设△OPA的面积为S.
(1)求S关于x的函数解析式;
(2)当S=4时,求P点的坐标.
20.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx+2(m+1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为3,求m值.
六、解答题(本题满分12分)
21.如图,在平面直角坐标系中,直线y=﹣x+3过点A(5,m)且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C.过点C且与y=2x平行的直线交y轴于点D.
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
七、解答题(本题满分12分)
22.预防新型冠状病毒期间,某种消毒液甲城需要7吨,乙城需要8吨,正好A地储备有10吨,B地储备有5吨,市预防新型冠状病毒领导小组决定将A、B两地储备的这15吨消毒液全部调往甲城和乙城,消毒液的运费价格如下表(单位:元/吨),设从A地调运x吨消毒液给甲城.
终点 起点 甲城 乙城
A地 100 120
B地 110 95
(1)根据题意,应从B地调运 吨消毒液给甲城,从B地调运 吨消毒液给乙城;(结果请用含x的代数式表示)
(2)求调运这15吨消毒液的总运费y关于x的函数关系式,并直接写出x的取值范围;
(3)求出总运费最低的调运方案,并算出最低运费.
八、解答题(本题满分14分)
23.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300km.
参考答案
一、选择题(共10小题).
1.函数y=中自变量x的取值范围是( )
A.x≠﹣4 B.x≠4 C.x≤﹣4 D.x≤4
解:由题意得,4﹣x≠0,
解得x≠4.
故选:B.
2.下列四个点中,恰好与点(﹣2,4)在同一个正比例函数图象上的是( )
A.(4,﹣2) B.(2,﹣4) C.(﹣4,2) D.(2,4)
解:设正比例函数的解析式为:y=kx,
把(﹣2,4)代入得:
4=﹣2k,
解得:k=﹣2,
即正比例函数的解析式为:y=﹣2x,
A.把x=4代入y=﹣2x得:y=﹣8,即A项错误,
B.把x=2代入y=﹣2x得:y=﹣4,即B项正确,
C.把x=﹣4代入y=﹣2x得:y=8,即C项错误,
D.把x=2代入y=﹣2x得:y=﹣4,即D项错误,
故选:B.
3.在下列各图象中,y是x的函数有( )
A.1个 B.2个 C.3个 D.4个
解:第一个、第二个、第三个图象y都是x的函数,第四个不是,共3个,
故选:C.
4.若点A(x1,﹣3),B(x2,﹣2),C(x3,1)在一次函数y=3x﹣b的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x1<x3 C.x3<x2<x1 D.x1<x3<x2
解:∵一次函数y=3x﹣b中,k=3>0,
∴y随x的增大而增大;
∵点A(x1,﹣3),B(x2,﹣2),C(x3,1),
∴x1<x2<x3;
故选:A.
5.在平面直角坐标系中,若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度后恰好经过点(﹣1,﹣2),则n的值为( )
A.10 B.8 C.5 D.3
解:∵若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度,
∴平移后的函数解析式为:y=﹣2x+6﹣n,
∵函数解y=﹣2x+6﹣n的图象经过点(﹣1,﹣2),
∴﹣2=﹣2×(﹣1)+6﹣n,
解得:n=10,
故选:A.
6.将直线y=2x+1向右平移2个单位.再向上平移2个单位后,得到直线y=kx+b.则下列关于直线y=kx+b的说法正确的是( )
A.与x轴交于(2,0) B.与y轴交于(0,﹣1)
C.y随x的增大而减小 D.经过第一、二、四象限
解:将直线y=2x+1向右平移2个单位.再向上平移2个单位后得到直线y=2x﹣1,
A、直线y=2x﹣1与x轴交于(2,0),错误;
B、直线y=2x﹣1与y轴交于(0,﹣1),正确
C、直线y=2x﹣1,y随x的增大而增大,错误;
D、直线y=2x﹣1经过第一、三、四象限,错误;
故选:B.
7.已知y是x的一次函数,下表中列出了部分对应值,则m等于( )
x ﹣1 0 1
y 1 m ﹣5
A.﹣1 B.0 C.﹣2 D.
解:设一次函数解析式为y=kx+b,
将x=﹣1,y=1;x=1,y=﹣5代入得:,
解得:k=﹣3,b=﹣2,
∴一次函数解析式为y=﹣3x﹣2,
令x=0,得到y=2,
则m=﹣2,
故选:C.
8.若点A(﹣2,a),B(b,)在同一个正比例函数图象上,则的值是( )
A. B.﹣3 C.3 D.﹣
解:设正比例函数解析式为y=kx,
∵点A(﹣2,a),B(b,)都在该函数图象上,
∴a=﹣2k,bk=,
即k=a,
∴,
∴ab=﹣3,
∴原式==,
故选:A.
9.两条直线y1=ax﹣b与y2=bx﹣a在同一坐标系中的图象可能是图中的( )
A. B.
C. D.
解:A:直线y1过第一、二、三象限,则a>0,b<0,直线y2过第一、二、四象限,则b<0,a<0,前后矛盾,故A选项错误;
B:直线y1过第一、二、三象限,则a>0,b<0,直线y2过第二、三、四象限,则b<0,a>0,故B选项正确;
C:直线y1过第一、三、四象限,则a>0,b>0,直线y2过第一、二、四象限,则b<0,a<0,前后矛盾,故C选项错误;
D:直线y1过第一、三、四象限,则a>0,b>0,直线y2过第二、三、四象限,则b<0,a>0,前后矛盾,故D选项错误;
故选:B.
10.如图①,在矩形ABCD中,动点P从A出发,以恒定的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x.△PAB面积为y,若y与x的函数图象如图②所示,则矩形ABCD的面积为( )
A.36 B.54 C.72 D.81
解:由题意及图②可知:
AB=6,BC=18﹣6=12,
∴矩形ABCD的面积为6×12=72.
故选:C.
二、填空题(每小题5分,共20分)
11.函数y=﹣2x+6,当函数值y=4时,自变量x的值是 1 .
解:当y=4时,﹣2x+6=4,
解得:x=1.
故答案为:1.
12.请写出一个一次函数 y=x+1 满足以下条件:(1)y随x的减小而减小;(2)图象与x轴交在负半轴上.
解:y=x+1满足条件y随x的减小而减小,图象与x轴交在负半轴上,
故答案为:y=x+1.
13.已知:一次函数y=(a+1)x﹣(a﹣2)中,该函数的图象不过第四象限,则a的范围是 ﹣1<a≤2 .
解:∵一次函数y=(a+1)x﹣(a﹣2)的图象不过第四象限,
∴,
解得﹣1<a≤2.
故答案为﹣1<a≤2.
14.某市出租车白天的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客白天乘坐出租车的路程x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 y=2.4x+6.8 .
解:依题意有:y=14+2.4(x﹣3)=2.4x+6.8.
故答案为:y=2.4x+6.8.
三、解答题(本答题共两小题,每题8分,满分16分)
15.已知直线m与直线y=2x+1平行,且经过(1,4).
(1)求直线m的解析式.
(2)求直线m与x轴的交点.
解:(1)设直线m为y=kx+b,
∵直线m与直线y=2x+1平行,
∴k=2,
把(1,4)代入y=2x+b得:b=2,
∴直线m的解析式为:y=2x+2;
(2)在直线m:y=2x+2中,令y=0,则2x+2=0,
解得x=﹣1,
∴直线m与x轴的交点为(﹣1,0).
16.已知y﹣2与x+3成正比例,且x=﹣4时,y=0.
(1)求y与x之间的函数关系式;
(2)点P1(2m﹣2,2m+1)在(1)中所得函数的图象上,求m的值.
解:(1)设y﹣2=k(x+3)(k≠0),
把x=﹣4,y=0代入得,0﹣2=k(﹣4+3),
解得,k=2,
∴y﹣2=2(x+3),
即:y=2x+8,
(2)∵点P1(2m﹣2,2m+1)在y=2x+8的图象上,
∴2m+1=2(2m﹣2)+8,
∴m=﹣,
四、解答题(本答题共两小题,每题8分,满分16分)
17.某汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.
(1)求y与x之间的函数关系.
(2)旅客最多可以免费携带多少千克的行李?
解:(1)设一次函数y=kx+b,
∵当x=60时,y=6,当x=90时,y=10,
∴ 解之,得,
∴所求函数关系式为y=x﹣2(x≥15);
(2)当y=0时,x﹣2=0,所以x=15,
故旅客最多可免费携带15kg行李.
18.某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
解:(1)设y甲=k1x,根据题意得5k1=100,解得k1=20,∴y甲=20x;
设y乙=k2x+100,根据题意得:20k2+100=300,解得k2=10,∴y乙=10x+100;
(2)①y甲<y乙,即20x<10x+100,解得x<10,当入园次数小于10次时,选择甲消费卡比较合算;
②y甲=y乙,即20x=10x+100,解得x=10,当入园次数等于10次时,选择两种消费卡费用一样;
③y甲>y乙,即20x>10x+100,解得x>10,当入园次数大于10次时,选择乙消费卡比较合算.
五、解答题(本答题共两小题,每题10分,满分20分)
19.已知点A(4,0)及在第一象限的动点P(x,y),且x+y=10,O为坐标原点,设△OPA的面积为S.
(1)求S关于x的函数解析式;
(2)当S=4时,求P点的坐标.
解:(1)如图所示,
∵x+y=10,
∴y=10﹣x,
∴S=×4×(10﹣x)=20﹣2x;
(2)由(1)知,S=20﹣2x,
∴20﹣2x=4,解得x=8,
∴y=2,
∴P(8,2).
20.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx+2(m+1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为3,求m值.
解:(1)当x≥0时,y=|x|=x,即y=x(x≥0),
将x=0代入得:y=0;
将x=1代入得:y=1,
当x≤0时,y=|x|=﹣x,即y=﹣x(x≤0),
将x=0代入得:y=0;
将x=﹣1代入得:y=1.
过点O(0,0),A(﹣1,1)作射线OA,过点O(0,0),B(1,1)作射线OB,
函数y=|x|的图象如图所示:
(2)∵y=mx+2(m+1)=m(x+2)+2,
∴x+2=0,y=2
∴x=﹣2,y=2,
即无论m取何值,函数y=mx+2(m+1)的图象经过的一个确定的点(﹣2,2);
(3)如下图:
∵函数y=mx+2(m+1)的图象经过顶点(﹣2,2)
∴OC==2.
∴OD?OC=3,
∴OD=,
所以点D的坐标为(,).
将x=,y=代入y=mx+2(m+1)得:m=﹣.
六、解答题(本题满分12分)
21.如图,在平面直角坐标系中,直线y=﹣x+3过点A(5,m)且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C.过点C且与y=2x平行的直线交y轴于点D.
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
解:(1)把A(5,m)代入y=﹣x+3得m=﹣5+3=﹣2,则A(5,﹣2),
∵点A向左平移2个单位,再向上平移4个单位,得到点C,
∴C(3,2),
∵过点C且与y=2x平行的直线交y轴于点D,
∴CD的解析式可设为y=2x+b,
把C(3,2)代入得6+b=2,解得b=﹣4,
∴直线CD的解析式为y=2x﹣4;
(2)当x=0时,y=﹣x+3=3,则B(0,3),
当y=0时,2x﹣4=0,解得x=2,则直线CD与x轴的交点坐标为(2,0);
易得CD平移到经过点B时的直线解析式为y=2x+3,
当y=0时,2x+3=0,解得x=﹣,则直线y=2x+3与x轴的交点坐标为(﹣,0),
∴直线CD在平移过程中与x轴交点的横坐标的取值范围为﹣≤x≤2.
七、解答题(本题满分12分)
22.预防新型冠状病毒期间,某种消毒液甲城需要7吨,乙城需要8吨,正好A地储备有10吨,B地储备有5吨,市预防新型冠状病毒领导小组决定将A、B两地储备的这15吨消毒液全部调往甲城和乙城,消毒液的运费价格如下表(单位:元/吨),设从A地调运x吨消毒液给甲城.
终点 起点 甲城 乙城
A地 100 120
B地 110 95
(1)根据题意,应从B地调运 (7﹣x) 吨消毒液给甲城,从B地调运 (x﹣2) 吨消毒液给乙城;(结果请用含x的代数式表示)
(2)求调运这15吨消毒液的总运费y关于x的函数关系式,并直接写出x的取值范围;
(3)求出总运费最低的调运方案,并算出最低运费.
解:(1)由题意可得,
从A地调运x吨消毒液给甲城,则调运(10﹣x)吨消毒液给乙城,从B地调运(7﹣x)吨消毒液给甲城,调运8﹣(10﹣x)=(x﹣2)吨消毒液给乙城,
故答案为:(7﹣x),(x﹣2);
(2)由题意可得,
y=100x+120(10﹣x)+110(7﹣x)+95(x﹣2)=﹣35x+1780,
∵,
∴2≤x≤7,
即总运费y关于x的函数关系式是y=﹣35x+1780(2≤x≤7);
(3)∵y=﹣35x+1780,
∴y随x的增大而减小,
∵2≤x≤7,
∴当x=7时,y取得最小值,此时y=1535,
即从A地调运7吨消毒液给甲城时,总运费最低,运费最低为1535元.
八、解答题(本题满分14分)
23.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)慢车的速度为 80 km/h,快车的速度为 120 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300km.
解:(1)(480﹣440)÷0.5=80km/h,
440÷(2.7﹣0.5)﹣80=120km/h,
所以,慢车速度为80km/h,
快车速度为120km/h;
故答案为:80;120.
(2)快车到达乙地(出发了4小时快车慢车相距360KM时甲车到达乙地);
∵快车走完全程所需时间为480÷120=4(h),
∴点D的横坐标为4.5,
纵坐标为(80+120)×(4.5﹣2.7)=360,
即点D(4.5,360);
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为300km.
即相遇前:(80+120)×(x﹣0.5)=440﹣300,
解得x=1.2(h),
相遇后:(80+120)×(x﹣2.7)=300,
解得x=4.2(h),
故x=1.2 h或4.2 h,两车之间的距离为300km.
