26.2.1 实际问题与反比例函数同步练习(含解析)
文档属性
| 名称 | 26.2.1 实际问题与反比例函数同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(一)(含答案)
一.选择题
1.某工厂现有原材料100吨,每天平均用去吨,这批原材料能用天,则与之间的函数表达式为
A. B. C. D.
2.如果等腰三角形的面积为10,底边长为,底边上的高为,则与的函数关系式为
A. B. C. D.
3.今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额(元与付款月数为正整数)之间的函数关系式是
A. B. C. D.
4.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为土石方的任务,该运输公司平均运送土石方的速度(单位:天)与完成运送任务所需时间(单位:天)之间的函数关系式是
A. B. C. D.
5.如图,曲线表示温度与时间之间的函数关系,它是一个反比例函数的图象的一支.当温度时,时间应
A.不小于 B.不大于 C.不小于 D.不大于
6.甲、乙两地相距200千米,则汽车从甲地到乙地所用的时间与汽车的平均速度之间的函数表达式为
A. B. C. D.
二.填空题
7.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点左侧固定位置处悬挂重物,在中点右侧用一个弹簧秤向下拉,改变弹簧秤与点的距离,观察弹簧秤的示数的变化情况.实验数据记录如下:
15 20 25
20 15 12
猜测与之间的函数关系,并求出函数关系式为 .
8.某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年 度 2008 2009 2010 2011
投入技术改进资金(万元) 2.5 3 4 4.5
产品成本(万元件) 7.2 6 4.5 4
9.如图,一定质量的氧气,其体积是密度的反比例函数,其图象如图,当时的氧气的体积 .
10.把一个长、 宽、 高分别为,,的长方体铜块铸成一个圆柱体铜块, 则该圆柱体铜块的底面积与高之间的函数关系式为 .
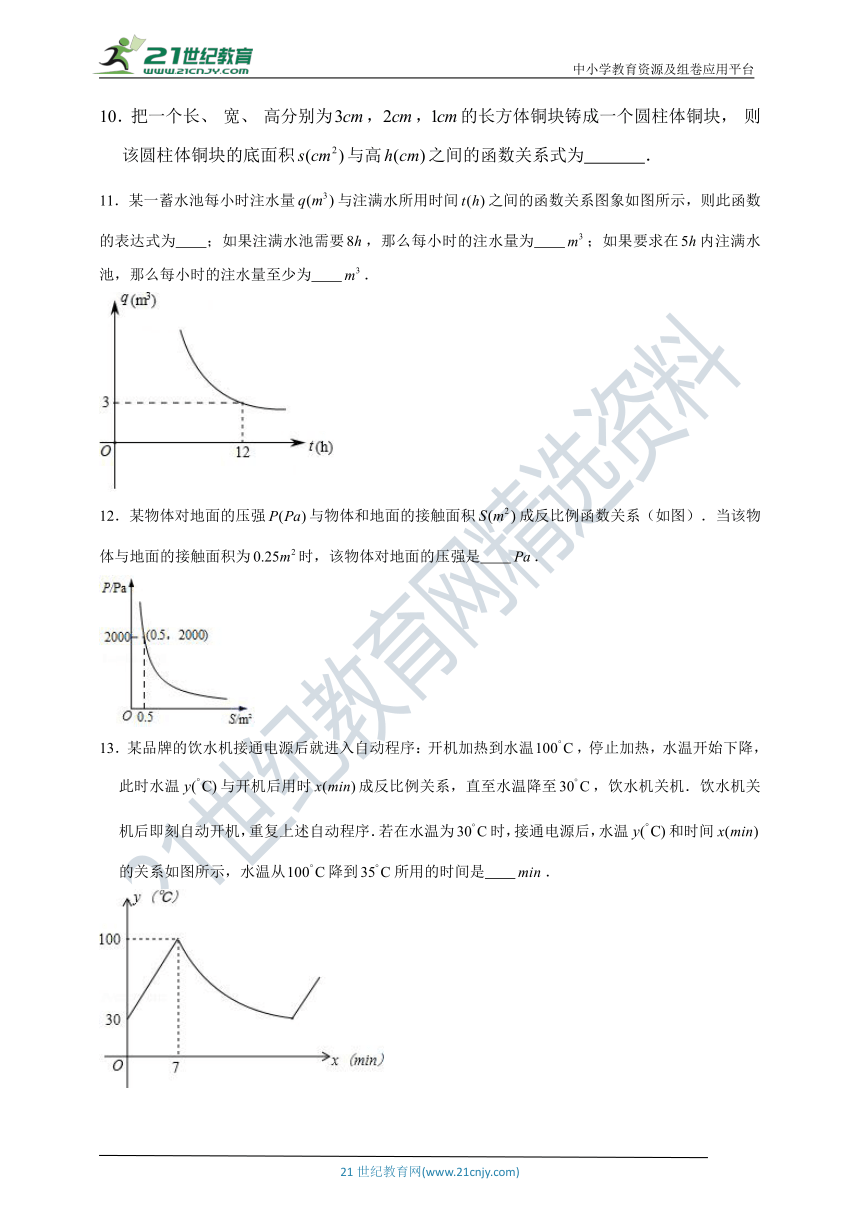
11.某一蓄水池每小时注水量与注满水所用时间之间的函数关系图象如图所示,则此函数的表达式为 ;如果注满水池需要,那么每小时的注水量为 ;如果要求在内注满水池,那么每小时的注水量至少为 .
12.某物体对地面的压强与物体和地面的接触面积成反比例函数关系(如图).当该物体与地面的接触面积为时,该物体对地面的压强是 .
13.某品牌的饮水机接通电源后就进入自动程序:开机加热到水温,停止加热,水温开始下降,此时水温与开机后用时成反比例关系,直至水温降至,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为时,接通电源后,水温和时间的关系如图所示,水温从降到所用的时间是 .
14.某气球内充满一定质量的气体,温度不变时,气球内气体的压强与气体的体积成反比例.当气体的体积时,气球内气体的压强.当气球内气体的压强大于时,气球就会爆炸.则气球内气体的体积应满足 ,气球才不会爆炸.
三.解答题
15.已知一个长方体的体积是,它的长是,宽是,高是.
(1)写出与之间的函数关系式;
(2)当时,求的值.
16.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数时,圆柱的底面积与高的关系;
(2)柳树乡共有耕地面积(单位:,该乡人均耕地面积(单位:人)与全乡总人口的关系.
17.环保局对某企业排污情况进行检测,当所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许值时,环保局要求该企业立即整改,必须在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度与时间(天的变化规律如图所示,其中线段表示前5天的变化规律,从第5天起,所排污水中硫化物的浓度与时间成反比例关系.
(1)求整改过程中硫化物的浓度与时间的函数表达式;
(2)该企业能否按期将排污整改达标?为什么?
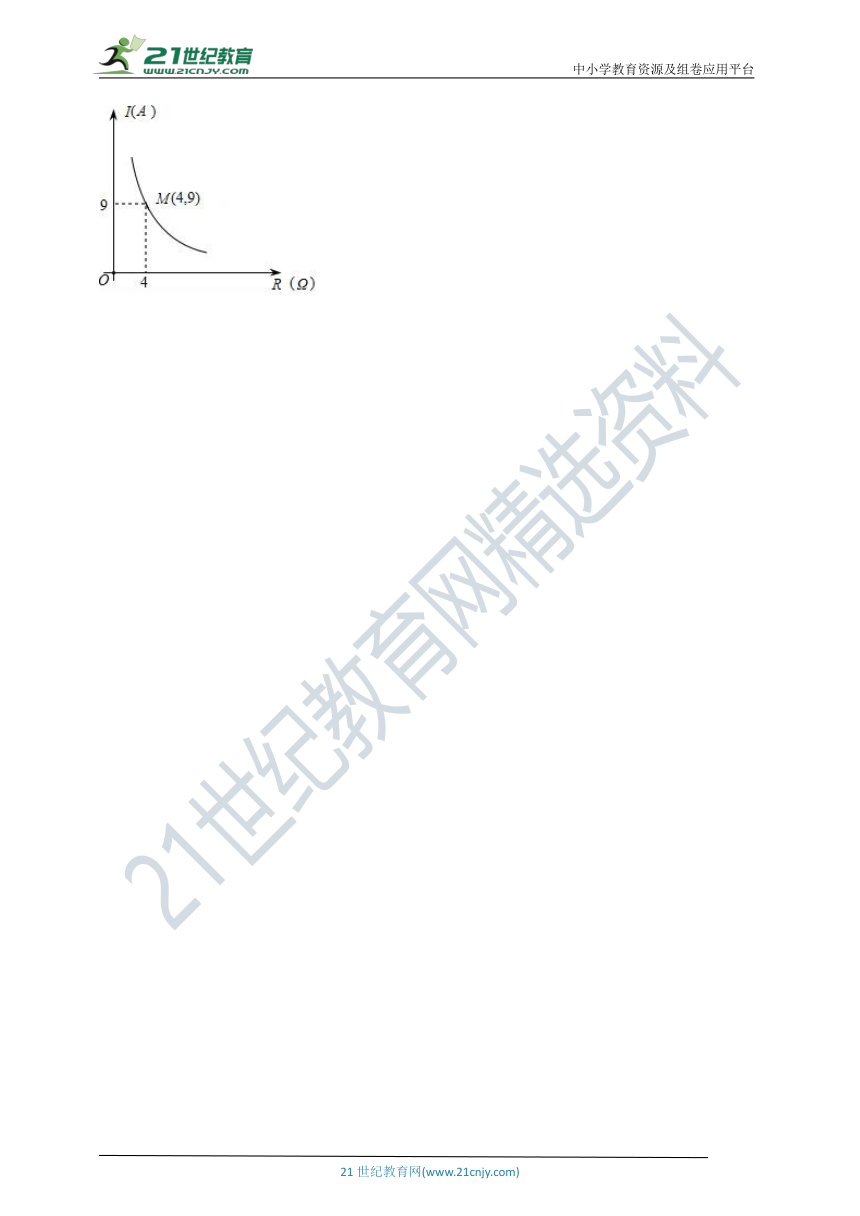
18.蓄电池的电压为定值,使用此电源时,电流(A)是电阻的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当时,求电流(A).
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(一)(含答案)
参考答案与试题解析
一.选择题
1.解:根据题意可得:.
故选:.
2.解:等腰三角形的面积为10,底边长为,底边上的高为,
,
与的函数关系式为:.
故选:.
3.解:由题意可得:.
故选:.
4.解:运送土石方总量平均运送土石方的速度完成运送任务所需时间,
,
,
故选:.
5.解:设函数解析式为,
经过点,
,
函数解析式为,
当时,,
故选:.
6.解:因为甲、乙两地相距200千米,汽车从甲地到乙地所用的时间与汽车的平均速度,
,
;
故选:.
二.填空题
7.解:由图象猜测与之间的函数关系为反比例函数,
设,
把,代入得:
,
将其余各点代入验证均适合,
与的函数关系式为:.
故答案为:.
8.解:有题意可得此函数解析式为反比例函数解析式,设其为解析式为.
当时,,
可得:,
解得
反比例函数是.
故答案为:.
9.解:设,
图象经过,
,
,
;
把代入可得:.
故答案为:6.
10.解: 由题意可得:,
则.
故答案为:.
11.解:设每小时注水量与注满水所用时间之间的函数关系为:,
把代入得:
,
故,
注满水池需要,
每小时的注水量为:,
要求在内注满水池,
每小时的注水量至少为:.
故答案为:,4.5,7.2.
12.解:设,把代入得:
,
故,
当时,
.
故答案为:4000.
13.解:开机加热时每分钟上升,
从到需要7分钟,
设一次函数关系式为:,
将,代入得,
,令,解得;
设反比例函数关系式为:,
将代入得,
,
将代入,解得;
水温从降到所用的时间是分钟,
故答案为:13.
14.解:设球内气体的气压和气体体积的关系式为.
当气体的体积时,气球内气体的压强,
,
,
,
当,即时,
.
故答案为:.
三.解答题
15.解:(1)由题意得,,
;
(2)当时,.
16.解:(1)由题意可得:;
(2)由题意可得:.
17.
解:(1)由图象知,点、的坐标分别为、,
当时,设的表达式为,
将点、的坐标代入上式得,解得,
故;
当时,设函数的表达式为,
把点的坐标代入上式并解得:,
故;
故函数的表达式为;
(2)不能,理由:
当时,,
故不能按期完成排污整改达标.
18.解:(1)由电流(A)是电阻的反比例函数,设,
把代入得:,
.
(2)当时,.
_21?????????è?????(www.21cnjy.com)_
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(一)(含答案)
一.选择题
1.某工厂现有原材料100吨,每天平均用去吨,这批原材料能用天,则与之间的函数表达式为
A. B. C. D.
2.如果等腰三角形的面积为10,底边长为,底边上的高为,则与的函数关系式为
A. B. C. D.
3.今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额(元与付款月数为正整数)之间的函数关系式是
A. B. C. D.
4.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为土石方的任务,该运输公司平均运送土石方的速度(单位:天)与完成运送任务所需时间(单位:天)之间的函数关系式是
A. B. C. D.
5.如图,曲线表示温度与时间之间的函数关系,它是一个反比例函数的图象的一支.当温度时,时间应
A.不小于 B.不大于 C.不小于 D.不大于
6.甲、乙两地相距200千米,则汽车从甲地到乙地所用的时间与汽车的平均速度之间的函数表达式为
A. B. C. D.
二.填空题
7.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点左侧固定位置处悬挂重物,在中点右侧用一个弹簧秤向下拉,改变弹簧秤与点的距离,观察弹簧秤的示数的变化情况.实验数据记录如下:
15 20 25
20 15 12
猜测与之间的函数关系,并求出函数关系式为 .
8.某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年 度 2008 2009 2010 2011
投入技术改进资金(万元) 2.5 3 4 4.5
产品成本(万元件) 7.2 6 4.5 4
9.如图,一定质量的氧气,其体积是密度的反比例函数,其图象如图,当时的氧气的体积 .
10.把一个长、 宽、 高分别为,,的长方体铜块铸成一个圆柱体铜块, 则该圆柱体铜块的底面积与高之间的函数关系式为 .
11.某一蓄水池每小时注水量与注满水所用时间之间的函数关系图象如图所示,则此函数的表达式为 ;如果注满水池需要,那么每小时的注水量为 ;如果要求在内注满水池,那么每小时的注水量至少为 .
12.某物体对地面的压强与物体和地面的接触面积成反比例函数关系(如图).当该物体与地面的接触面积为时,该物体对地面的压强是 .
13.某品牌的饮水机接通电源后就进入自动程序:开机加热到水温,停止加热,水温开始下降,此时水温与开机后用时成反比例关系,直至水温降至,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为时,接通电源后,水温和时间的关系如图所示,水温从降到所用的时间是 .
14.某气球内充满一定质量的气体,温度不变时,气球内气体的压强与气体的体积成反比例.当气体的体积时,气球内气体的压强.当气球内气体的压强大于时,气球就会爆炸.则气球内气体的体积应满足 ,气球才不会爆炸.
三.解答题
15.已知一个长方体的体积是,它的长是,宽是,高是.
(1)写出与之间的函数关系式;
(2)当时,求的值.
16.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数时,圆柱的底面积与高的关系;
(2)柳树乡共有耕地面积(单位:,该乡人均耕地面积(单位:人)与全乡总人口的关系.
17.环保局对某企业排污情况进行检测,当所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许值时,环保局要求该企业立即整改,必须在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度与时间(天的变化规律如图所示,其中线段表示前5天的变化规律,从第5天起,所排污水中硫化物的浓度与时间成反比例关系.
(1)求整改过程中硫化物的浓度与时间的函数表达式;
(2)该企业能否按期将排污整改达标?为什么?
18.蓄电池的电压为定值,使用此电源时,电流(A)是电阻的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当时,求电流(A).
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(一)(含答案)
参考答案与试题解析
一.选择题
1.解:根据题意可得:.
故选:.
2.解:等腰三角形的面积为10,底边长为,底边上的高为,
,
与的函数关系式为:.
故选:.
3.解:由题意可得:.
故选:.
4.解:运送土石方总量平均运送土石方的速度完成运送任务所需时间,
,
,
故选:.
5.解:设函数解析式为,
经过点,
,
函数解析式为,
当时,,
故选:.
6.解:因为甲、乙两地相距200千米,汽车从甲地到乙地所用的时间与汽车的平均速度,
,
;
故选:.
二.填空题
7.解:由图象猜测与之间的函数关系为反比例函数,
设,
把,代入得:
,
将其余各点代入验证均适合,
与的函数关系式为:.
故答案为:.
8.解:有题意可得此函数解析式为反比例函数解析式,设其为解析式为.
当时,,
可得:,
解得
反比例函数是.
故答案为:.
9.解:设,
图象经过,
,
,
;
把代入可得:.
故答案为:6.
10.解: 由题意可得:,
则.
故答案为:.
11.解:设每小时注水量与注满水所用时间之间的函数关系为:,
把代入得:
,
故,
注满水池需要,
每小时的注水量为:,
要求在内注满水池,
每小时的注水量至少为:.
故答案为:,4.5,7.2.
12.解:设,把代入得:
,
故,
当时,
.
故答案为:4000.
13.解:开机加热时每分钟上升,
从到需要7分钟,
设一次函数关系式为:,
将,代入得,
,令,解得;
设反比例函数关系式为:,
将代入得,
,
将代入,解得;
水温从降到所用的时间是分钟,
故答案为:13.
14.解:设球内气体的气压和气体体积的关系式为.
当气体的体积时,气球内气体的压强,
,
,
,
当,即时,
.
故答案为:.
三.解答题
15.解:(1)由题意得,,
;
(2)当时,.
16.解:(1)由题意可得:;
(2)由题意可得:.
17.
解:(1)由图象知,点、的坐标分别为、,
当时,设的表达式为,
将点、的坐标代入上式得,解得,
故;
当时,设函数的表达式为,
把点的坐标代入上式并解得:,
故;
故函数的表达式为;
(2)不能,理由:
当时,,
故不能按期完成排污整改达标.
18.解:(1)由电流(A)是电阻的反比例函数,设,
把代入得:,
.
(2)当时,.
_21?????????è?????(www.21cnjy.com)_
