教科版_选修3-2_5. 电磁感应中的能量转化与守恒课件28张PPT
文档属性
| 名称 | 教科版_选修3-2_5. 电磁感应中的能量转化与守恒课件28张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 472.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-16 14:20:55 | ||
图片预览






文档简介
电磁感应中的能量转化
与守恒
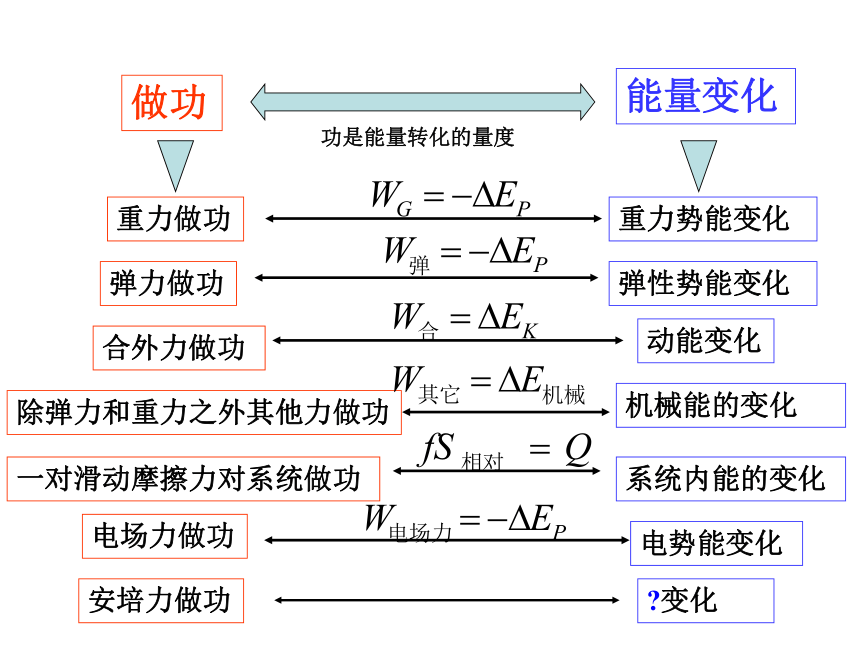
做功
能量变化
重力做功
重力势能变化
弹力做功
弹性势能变化
合外力做功
动能变化
除弹力和重力之外其他力做功
机械能的变化
一对滑动摩擦力对系统做功
系统内能的变化
电场力做功
电势能变化
功是能量转化的量度
安培力做功
?变化
I
F安
a
b
c
d
e
f
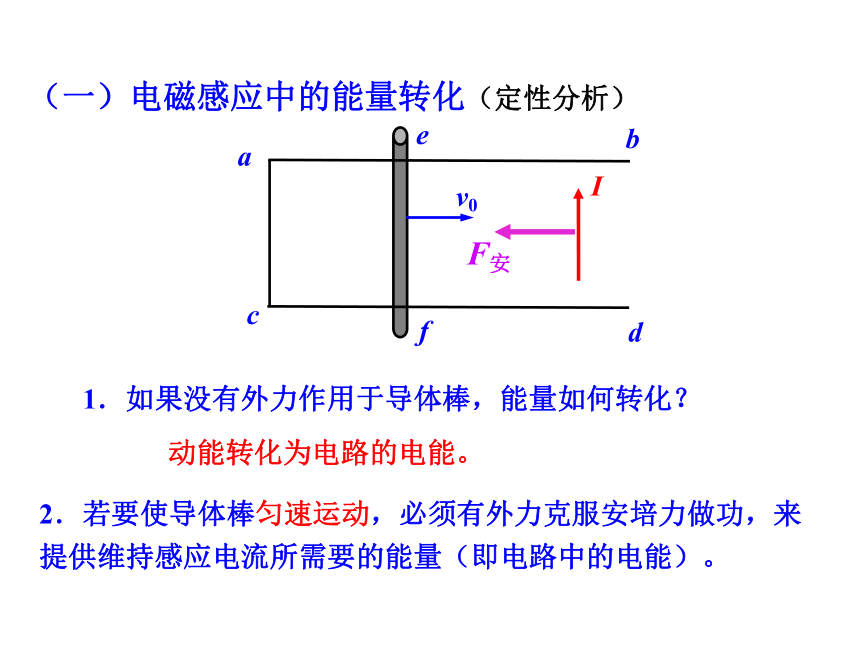
1.如果没有外力作用于导体棒,能量如何转化?
(一)电磁感应中的能量转化(定性分析)
v0
动能转化为电路的电能。
2.若要使导体棒匀速运动,必须有外力克服安培力做功,来提供维持感应电流所需要的能量(即电路中的电能)。
I
F安
a
b
c
d
e
f
1.导体棒在安培力作用下向右减速切割磁感线运动;
(二)电磁感应中的能量转化(定量分析)
对导体棒,动能定理:
对整个回路,能量守恒:
v0
则:
克服安培力做了多少功,就有多少电能产生。
I
F安
a
b
c
d
e
f
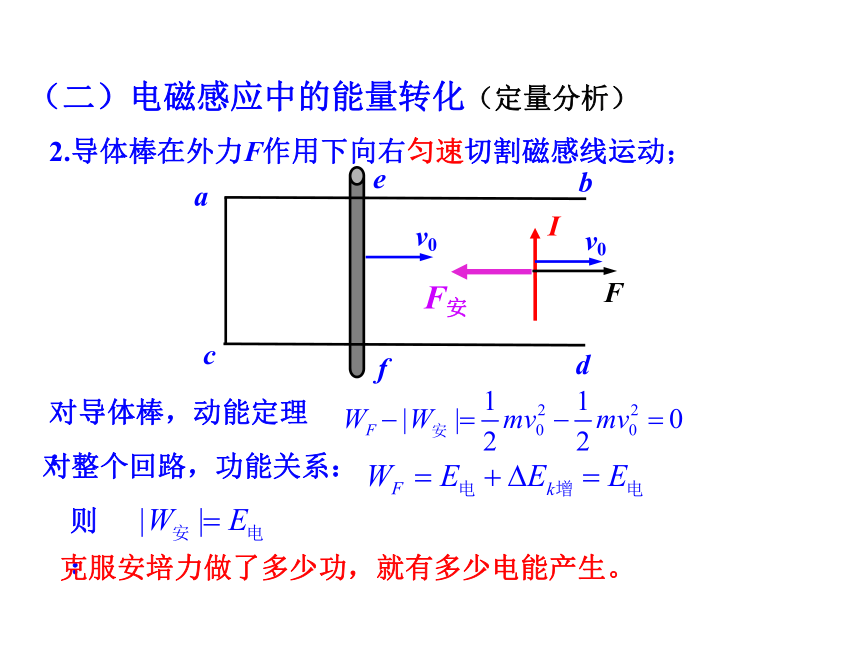
2.导体棒在外力F作用下向右匀速切割磁感线运动;
(二)电磁感应中的能量转化(定量分析)
对导体棒,动能定理:
F
对整个回路,功能关系:
则:
克服安培力做了多少功,就有多少电能产生。
v0
v0
I
F安
a
b
c
d
e
f
3.导体棒在外力F作用下向右加速切割磁感线运动;
(二)电磁感应中的能量转化(定量分析)
对导体棒,动能定理:
F
对整个回路,功能关系:
则:
克服安培力做了多少功,就有多少电能产生。
v0
v
在切割磁感线的电磁感应中,产生的电能是通过外力克服安培力做功转化而来的,克服安培力做了多少功,就有多少电能产生。克服安培力做功的过程,也是机械能转化为电能的过程,是机械能借助于电磁感应实现了向电能的转化。而这些电能又通过感应电流做功,转化为其他形式的能。
I
F
a
b
c
d
e
f
例1、如图,金属棒ef以v=2m/s的速度沿导轨向右匀速运动,导轨的宽度L=0.5m,匀强磁场的磁感应强度B=1T,导体棒的电阻R=1Ω,导轨电阻不计。为了保持导体棒匀速运动,求外力做功的功率和感应电流的电功率。
1.用法拉第电磁感应定律和楞次定律确定感应电动势的大
小和方向。
2.画出等效电路图,求出回路中电阻消耗的电功率表达式。
3.分析导体机械能的变化,用能量守恒关系得到机械功
率的改变与回路中电功率的改变所满足的方程。
解这类问题的一般步骤:
练习1. 在磁感应强度为B的垂直纸面向外的匀强磁场中,竖直放置一个 形金属框ABCD,框面垂直于磁场,宽BC=L,质量为m的金属杆PQ用光滑金属套连接在框架AB和CD上如图.金属杆PQ电阻为R,金属框电阻不计。当杆自静止开始沿框架下滑时
(1)开始下滑的加速度是多少?
(2)框内感应电流的方向怎样?
(3)金属杆下滑的最大速度是多少?
(4)从开始下滑到达到最大速度过程中
重力势能转化为什么能量?
Q
B
P
C
D
A
mg
Q
B
P
C
D
A
mg
I
F
练习2、如图甲所示,足够长的金属导轨竖直放在水平方向的匀强磁场中,导体棒MN可以在导轨上无摩擦的滑动。已知匀强磁场的磁感应强度B=0.4T,导轨间距为L=0.1m,导体棒MN的质量为m=6g且电阻r=0.1Ω,电阻R=0.3Ω,其他电阻不计,(g取10m/s2)求:
(1)导体棒MN下滑的最大速度多大?
(2)导体棒MN下滑达到最大速度后,棒
克服安培力做功的功率,电阻R消耗的功
率和电阻r消耗的功率为多大?
练习3、如图所示,MN为金属杆,在竖直平面上贴着光滑
的金属导轨下滑,导轨间距L=0.1m,导轨上端接有电阻R
=0.5Ω,导轨与金属杆电阻均不计,整个装置处于磁感
应强度B=0.5T的水平匀强磁场中.若杆MN以稳定速度下滑
时,每秒有0.02J的重力势能转化为电能,则MN杆下滑速
度v= m/s.
2
v
R
N
M
练习4、竖直放置的平行光滑导轨,其电阻不计,磁场方向如图所示,磁感应强度B=0.5T,导体ab及cd长均为0.2m,电阻均为0.1Ω,重均为0.1N,现用力向上推动导体ab,使之匀速上升(与导轨接触良好),此时,cd恰
好静止不动,那么ab上升时,下列说
法正确的是( )
A.ab受到的推力大小为0.2N
B.ab 向上的速度为2m/s
C.在2s内,推力做功转化的电能是0.4J
D.在2s内,推力做功为0.6J
d
c
b
a
mg
F1
mg
F
F1
ABC
例2、如图所示,质量为m,边长为L的正方形线框,在有界匀强磁场上方h高处由静止自由下落,线框的总电阻为R,磁感应强度为B的匀强磁场宽度为2L。线框下落过程中,ab边始终与磁场边界平行且处于水平方向,已知ab边刚穿出磁
场时线框恰好做匀速运动,求:
(1)cd边刚进入磁场时线框的
速度。
(2)线框穿过磁场的过程中,
产生的焦耳热。
总结:电磁感应现象实质是不同形式的能量相互转化的过程,理清能量转化过程,用“能量”观点研究问题,往往比较简单。且导体棒加速时,电流是变化的,不能直接用Q=I2Rt求解(时间也无法确定),因而用能量守恒的知识来解决。
练习5、如图所示,电阻为R的矩形线框,长为L,宽为a,在外力作用下,以恒定速度v向右运动,通过宽度为d,磁感应强度为B的匀强磁场,在下列两种情况下求外力做的功:
(a)Ld时。
d
B
L
a
解:感应电动势E=BLV
由电路欧姆定律 I=E/R
安培力F=BIL
匀速运动,受力平衡,F=F安
由W=Fs
当Ld
B
L
a
当L>d时有W=2B2a2dv/R
练习6、如图所示,把矩形线框先后以不同的速度v1和 v2匀速地完全拉出有界匀强磁场.设线框电阻为R,且两次的始末位置相同,求(1)通过导线截面的电量之比
(2)两次拉出过程外力做功之比
(3)两次拉出过程中电流的功率之比
v
B
(1)q=IΔt= EΔt/R=ΔΦ/R
则q1/q2=1
W=FL=BIlL=B2l2vL/R∝v
W1/W2=v1/v2
P=E2/R = B2l2v2/R∝v2
则P1/P2=v12/v22
解:
练习7、电阻为R的矩形导线框abcd,边长ab=l, ad=h,质量为m,自某一高度自由落体,通过一匀强磁场,磁场方向垂直纸面向里,磁场区域的宽度为h ,如图,
若线框恰好以恒定速度通过磁场,线
框内产生的焦耳热等于 .
(不考虑空气阻力)
l
h
h
a
b
c
d
解: 由能量守恒定律,线框通过磁场时减少的重力势能转化为线框的内能,
所以 Q=2mgh
2mgh
例3、如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距lm,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.求(1)金属棒沿导轨由静止开始下滑时的加速度大小;(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8W,求该速度的大小;(3)在上问中,若
R=2Ω,金属棒中的电流方向由a到b,
求磁感应强度的大小方向.(g=10m/s2,
sin37°=0.6,cos37°=0.8)
a
b
R
θ
θ
由①式解得a=10×(0.6-0.25×0.8)m/s2=4m/s2 ②
解:(1)金属棒开始下滑的初速度为零,根据牛顿第二定律
mgsinθ-μmgcosθ=ma ①
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向上受力平衡
mgsinθ-μmgcosθ-F=0 ③
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的
电功率 Fv=P ④
由③、④得
(3)设电路中电流为I,两导轨间金属棒的长为L,磁场的磁感应强度为B I=BLv/R ⑥
P=I2R ⑦
由⑥、⑦两式解得
磁场方向垂直导轨平面向上
练习8、 倾角为30°的斜面上,有一导体框架,宽为1m,不计电阻,垂直斜面的匀强磁场磁感应强度为0.2T,置于框架上的金属杆ab,质量为0.2kg,电阻0.1Ω,如图所示.不计摩擦,当金属杆ab由静止下滑时,求:
(1)当杆的速度达到2m/s时,ab两端的电压;
(2)回路中的最大电流和功率.
30
b
a
B
L
N
F
mg
解:
(1)E=BLv=0.4V I=E/R=4A
因为外电阻等于0,所以U=0
(2)达到最大速度时,
BImL=mgsin30
Im=mgsin30??/BL=1/0.2=5
Pm=Im2R=25??0.1=2.5
练习9、如图,两根光滑的金属导轨,平行放置在倾角为θ斜
面上,导轨的左端接有电阻R,导轨自身的电阻忽略不计。斜
面处于匀强磁场中,磁场方向垂直于斜面向上。质量为m,电
阻可不计的金属棒ab,在沿着斜面与棒垂直的恒力作用下沿
导轨匀速上滑,并上升h高度,如图所示。在这过程中 ( )
A.作用于金属棒上的各个力的合力所做的功等于零
B.作用于金属棒上的各个力的合力所做的功等于
mgh与电阻R上发出的焦耳热之和
C.恒力F与安培力的合力所做的功等于零
D.恒力F与重力的合力所做的功等于电阻R
上发出的焦耳热
AD
1.能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为其他形式,或者从一个物体转移到另一个物体,在转化或转移的过程中,能量的总量不变,这就是能量守恒定律 。
2.在电磁感应中,产生的电能是通过外力克服安培力做功转化而来的,外力做了多少功,就有多少电能产生。克服安培力做功的过程,也是机械能转化为电能的过程。
(1)用法拉第电磁感应定律和楞次定律确定感应电动势
的大小和方向。
(2)画出等效电路图,求出回路中电流强度,电阻消耗的电功率表达式。
(3)分析导体机械能的变化,用能量守恒关系得到机械
功率的改变与回路中电功率的改变所满足的方程。
3.解决这类问题的一般步骤:
与守恒
做功
能量变化
重力做功
重力势能变化
弹力做功
弹性势能变化
合外力做功
动能变化
除弹力和重力之外其他力做功
机械能的变化
一对滑动摩擦力对系统做功
系统内能的变化
电场力做功
电势能变化
功是能量转化的量度
安培力做功
?变化
I
F安
a
b
c
d
e
f
1.如果没有外力作用于导体棒,能量如何转化?
(一)电磁感应中的能量转化(定性分析)
v0
动能转化为电路的电能。
2.若要使导体棒匀速运动,必须有外力克服安培力做功,来提供维持感应电流所需要的能量(即电路中的电能)。
I
F安
a
b
c
d
e
f
1.导体棒在安培力作用下向右减速切割磁感线运动;
(二)电磁感应中的能量转化(定量分析)
对导体棒,动能定理:
对整个回路,能量守恒:
v0
则:
克服安培力做了多少功,就有多少电能产生。
I
F安
a
b
c
d
e
f
2.导体棒在外力F作用下向右匀速切割磁感线运动;
(二)电磁感应中的能量转化(定量分析)
对导体棒,动能定理:
F
对整个回路,功能关系:
则:
克服安培力做了多少功,就有多少电能产生。
v0
v0
I
F安
a
b
c
d
e
f
3.导体棒在外力F作用下向右加速切割磁感线运动;
(二)电磁感应中的能量转化(定量分析)
对导体棒,动能定理:
F
对整个回路,功能关系:
则:
克服安培力做了多少功,就有多少电能产生。
v0
v
在切割磁感线的电磁感应中,产生的电能是通过外力克服安培力做功转化而来的,克服安培力做了多少功,就有多少电能产生。克服安培力做功的过程,也是机械能转化为电能的过程,是机械能借助于电磁感应实现了向电能的转化。而这些电能又通过感应电流做功,转化为其他形式的能。
I
F
a
b
c
d
e
f
例1、如图,金属棒ef以v=2m/s的速度沿导轨向右匀速运动,导轨的宽度L=0.5m,匀强磁场的磁感应强度B=1T,导体棒的电阻R=1Ω,导轨电阻不计。为了保持导体棒匀速运动,求外力做功的功率和感应电流的电功率。
1.用法拉第电磁感应定律和楞次定律确定感应电动势的大
小和方向。
2.画出等效电路图,求出回路中电阻消耗的电功率表达式。
3.分析导体机械能的变化,用能量守恒关系得到机械功
率的改变与回路中电功率的改变所满足的方程。
解这类问题的一般步骤:
练习1. 在磁感应强度为B的垂直纸面向外的匀强磁场中,竖直放置一个 形金属框ABCD,框面垂直于磁场,宽BC=L,质量为m的金属杆PQ用光滑金属套连接在框架AB和CD上如图.金属杆PQ电阻为R,金属框电阻不计。当杆自静止开始沿框架下滑时
(1)开始下滑的加速度是多少?
(2)框内感应电流的方向怎样?
(3)金属杆下滑的最大速度是多少?
(4)从开始下滑到达到最大速度过程中
重力势能转化为什么能量?
Q
B
P
C
D
A
mg
Q
B
P
C
D
A
mg
I
F
练习2、如图甲所示,足够长的金属导轨竖直放在水平方向的匀强磁场中,导体棒MN可以在导轨上无摩擦的滑动。已知匀强磁场的磁感应强度B=0.4T,导轨间距为L=0.1m,导体棒MN的质量为m=6g且电阻r=0.1Ω,电阻R=0.3Ω,其他电阻不计,(g取10m/s2)求:
(1)导体棒MN下滑的最大速度多大?
(2)导体棒MN下滑达到最大速度后,棒
克服安培力做功的功率,电阻R消耗的功
率和电阻r消耗的功率为多大?
练习3、如图所示,MN为金属杆,在竖直平面上贴着光滑
的金属导轨下滑,导轨间距L=0.1m,导轨上端接有电阻R
=0.5Ω,导轨与金属杆电阻均不计,整个装置处于磁感
应强度B=0.5T的水平匀强磁场中.若杆MN以稳定速度下滑
时,每秒有0.02J的重力势能转化为电能,则MN杆下滑速
度v= m/s.
2
v
R
N
M
练习4、竖直放置的平行光滑导轨,其电阻不计,磁场方向如图所示,磁感应强度B=0.5T,导体ab及cd长均为0.2m,电阻均为0.1Ω,重均为0.1N,现用力向上推动导体ab,使之匀速上升(与导轨接触良好),此时,cd恰
好静止不动,那么ab上升时,下列说
法正确的是( )
A.ab受到的推力大小为0.2N
B.ab 向上的速度为2m/s
C.在2s内,推力做功转化的电能是0.4J
D.在2s内,推力做功为0.6J
d
c
b
a
mg
F1
mg
F
F1
ABC
例2、如图所示,质量为m,边长为L的正方形线框,在有界匀强磁场上方h高处由静止自由下落,线框的总电阻为R,磁感应强度为B的匀强磁场宽度为2L。线框下落过程中,ab边始终与磁场边界平行且处于水平方向,已知ab边刚穿出磁
场时线框恰好做匀速运动,求:
(1)cd边刚进入磁场时线框的
速度。
(2)线框穿过磁场的过程中,
产生的焦耳热。
总结:电磁感应现象实质是不同形式的能量相互转化的过程,理清能量转化过程,用“能量”观点研究问题,往往比较简单。且导体棒加速时,电流是变化的,不能直接用Q=I2Rt求解(时间也无法确定),因而用能量守恒的知识来解决。
练习5、如图所示,电阻为R的矩形线框,长为L,宽为a,在外力作用下,以恒定速度v向右运动,通过宽度为d,磁感应强度为B的匀强磁场,在下列两种情况下求外力做的功:
(a)L
d
B
L
a
解:感应电动势E=BLV
由电路欧姆定律 I=E/R
安培力F=BIL
匀速运动,受力平衡,F=F安
由W=Fs
当L
B
L
a
当L>d时有W=2B2a2dv/R
练习6、如图所示,把矩形线框先后以不同的速度v1和 v2匀速地完全拉出有界匀强磁场.设线框电阻为R,且两次的始末位置相同,求(1)通过导线截面的电量之比
(2)两次拉出过程外力做功之比
(3)两次拉出过程中电流的功率之比
v
B
(1)q=IΔt= EΔt/R=ΔΦ/R
则q1/q2=1
W=FL=BIlL=B2l2vL/R∝v
W1/W2=v1/v2
P=E2/R = B2l2v2/R∝v2
则P1/P2=v12/v22
解:
练习7、电阻为R的矩形导线框abcd,边长ab=l, ad=h,质量为m,自某一高度自由落体,通过一匀强磁场,磁场方向垂直纸面向里,磁场区域的宽度为h ,如图,
若线框恰好以恒定速度通过磁场,线
框内产生的焦耳热等于 .
(不考虑空气阻力)
l
h
h
a
b
c
d
解: 由能量守恒定律,线框通过磁场时减少的重力势能转化为线框的内能,
所以 Q=2mgh
2mgh
例3、如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距lm,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.求(1)金属棒沿导轨由静止开始下滑时的加速度大小;(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8W,求该速度的大小;(3)在上问中,若
R=2Ω,金属棒中的电流方向由a到b,
求磁感应强度的大小方向.(g=10m/s2,
sin37°=0.6,cos37°=0.8)
a
b
R
θ
θ
由①式解得a=10×(0.6-0.25×0.8)m/s2=4m/s2 ②
解:(1)金属棒开始下滑的初速度为零,根据牛顿第二定律
mgsinθ-μmgcosθ=ma ①
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向上受力平衡
mgsinθ-μmgcosθ-F=0 ③
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的
电功率 Fv=P ④
由③、④得
(3)设电路中电流为I,两导轨间金属棒的长为L,磁场的磁感应强度为B I=BLv/R ⑥
P=I2R ⑦
由⑥、⑦两式解得
磁场方向垂直导轨平面向上
练习8、 倾角为30°的斜面上,有一导体框架,宽为1m,不计电阻,垂直斜面的匀强磁场磁感应强度为0.2T,置于框架上的金属杆ab,质量为0.2kg,电阻0.1Ω,如图所示.不计摩擦,当金属杆ab由静止下滑时,求:
(1)当杆的速度达到2m/s时,ab两端的电压;
(2)回路中的最大电流和功率.
30
b
a
B
L
N
F
mg
解:
(1)E=BLv=0.4V I=E/R=4A
因为外电阻等于0,所以U=0
(2)达到最大速度时,
BImL=mgsin30
Im=mgsin30??/BL=1/0.2=5
Pm=Im2R=25??0.1=2.5
练习9、如图,两根光滑的金属导轨,平行放置在倾角为θ斜
面上,导轨的左端接有电阻R,导轨自身的电阻忽略不计。斜
面处于匀强磁场中,磁场方向垂直于斜面向上。质量为m,电
阻可不计的金属棒ab,在沿着斜面与棒垂直的恒力作用下沿
导轨匀速上滑,并上升h高度,如图所示。在这过程中 ( )
A.作用于金属棒上的各个力的合力所做的功等于零
B.作用于金属棒上的各个力的合力所做的功等于
mgh与电阻R上发出的焦耳热之和
C.恒力F与安培力的合力所做的功等于零
D.恒力F与重力的合力所做的功等于电阻R
上发出的焦耳热
AD
1.能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为其他形式,或者从一个物体转移到另一个物体,在转化或转移的过程中,能量的总量不变,这就是能量守恒定律 。
2.在电磁感应中,产生的电能是通过外力克服安培力做功转化而来的,外力做了多少功,就有多少电能产生。克服安培力做功的过程,也是机械能转化为电能的过程。
(1)用法拉第电磁感应定律和楞次定律确定感应电动势
的大小和方向。
(2)画出等效电路图,求出回路中电流强度,电阻消耗的电功率表达式。
(3)分析导体机械能的变化,用能量守恒关系得到机械
功率的改变与回路中电功率的改变所满足的方程。
3.解决这类问题的一般步骤:
