19.1 勾股定理
图片预览






文档简介
(共37张PPT)
19.1 勾股定理
这就是本届大会会徽的图案.
你见过这个图案吗?
你听说过勾股定理吗?
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
这个图形里蕴涵着怎样博大精深的知识呢?
它标志着我国古代数学的伟大成就!
邮票赏析
这是1955年希腊为纪念一位数学家曾经发行的邮票。
3
4
5
邮票的秘密
观察这枚邮票图案小方格的个数,
你有什么发现
3 +4 =5
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,
相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上
,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看
着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块
直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人
看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥
拉斯恍然大悟的样子,站起来,大笑着跑回家去了.
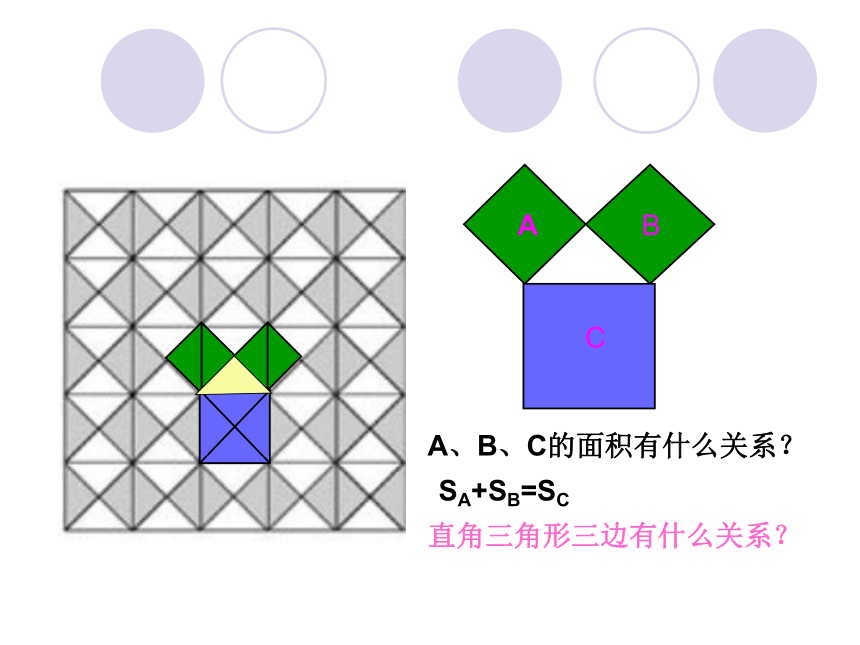
同学们,我们也来观察下面图中的地面,看看你能
发现什么?是否也和大哲学家有同样的发现呢?
A
B
C
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
B
A
C
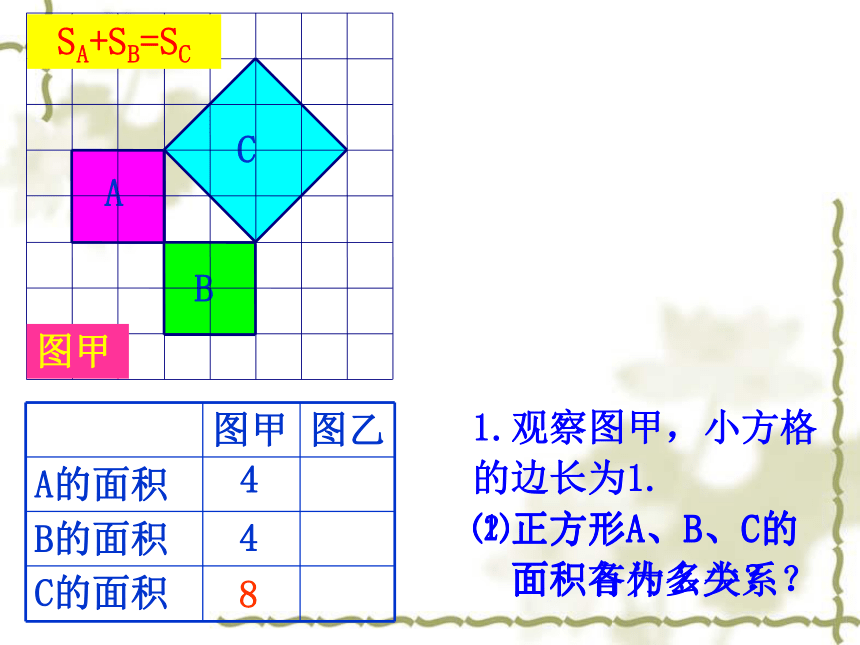
图甲 图乙
A的面积
B的面积
C的面积
4
4
8
SA+SB=SC
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
A
B
C
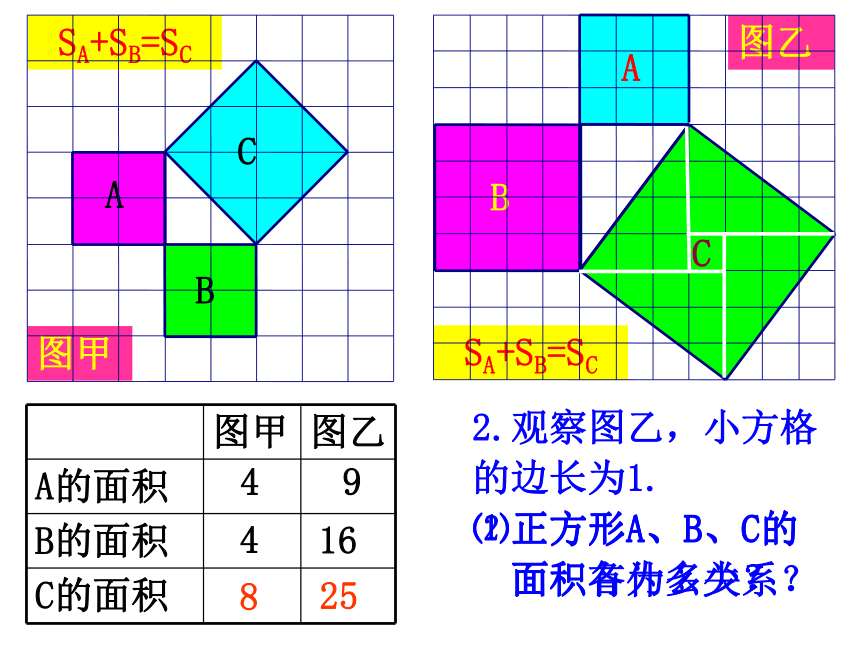
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
A
B
图乙
2.观察图乙,小方格
的边长为1.
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
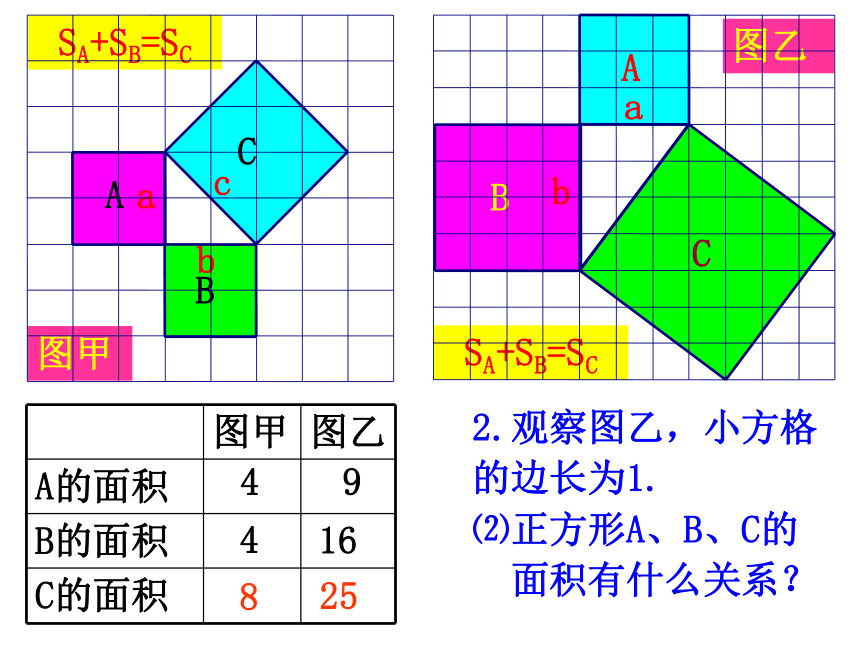
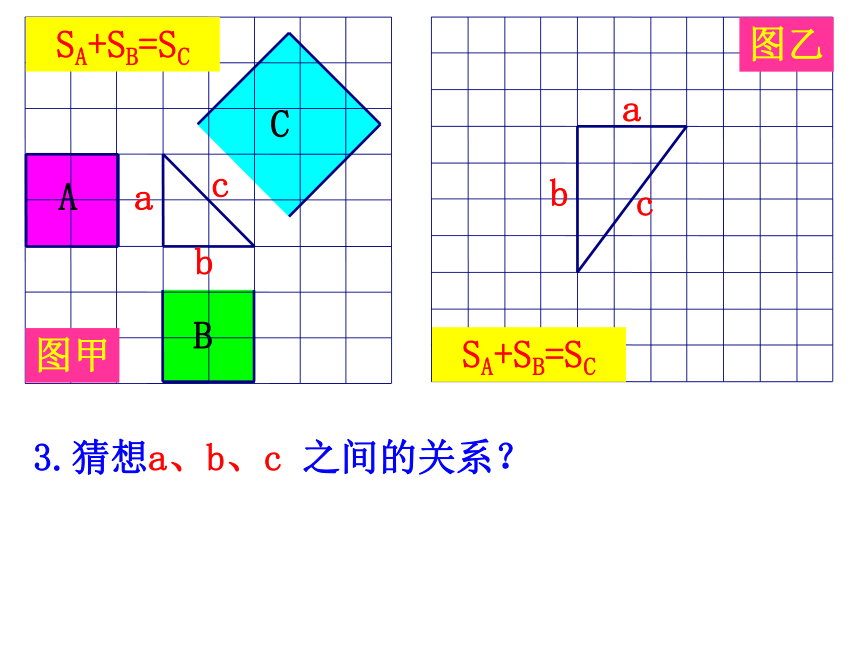
a
b
c
a
b
c
C
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
3.猜想a、b、c 之间的关系?
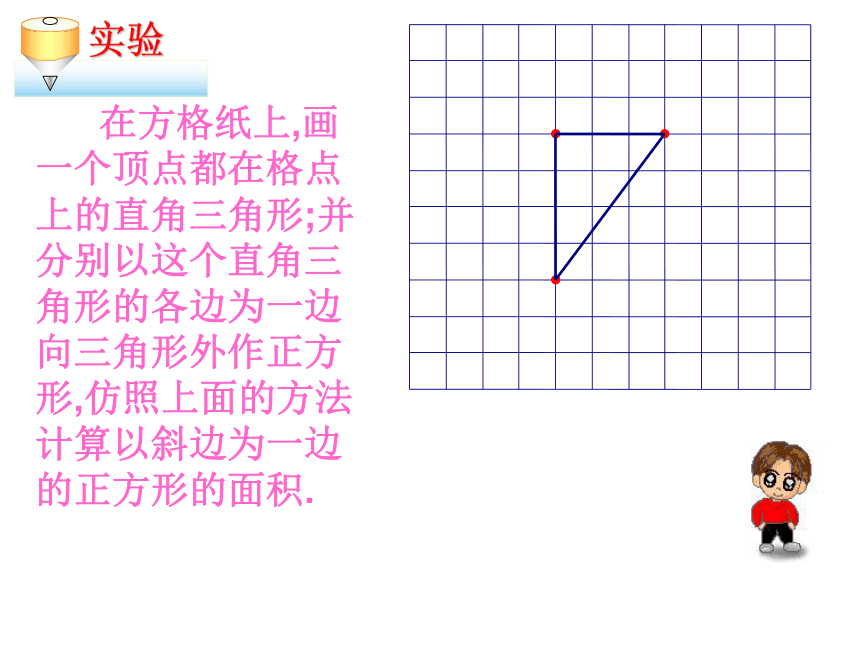
在方格纸上,画
一个顶点都在格点
上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方
形,仿照上面的方法
计算以斜边为一边的正方形的面积.
实验
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
以正方形为基础证明1
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab =c2+2ab
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
a
b
c
证明:
∵ s大正方形=
s大正方形 =
以正方形为基础证明2
c
4× ab+(b-a)
=2ab+b -2ab+b
=a +b
又∵S大正方形=S大正方形
∴c =a +b
a
a
b
b
c
c
∵ s梯形= (a+b)(a+b)= (a2+2ab+b2)
= a2+ab+ b2
s梯形=2× ab+ c2=ab+ c2
∵s梯形=s梯形 ∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
美国第二十任总统伽菲尔德的证法
在数学史上被传为佳话
勾股定理(毕达哥拉斯定理)
(gou-gu theorem)
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于
斜边的平方.
a
c
勾
弦
b
股
结论变形
a2 + b2 = c2
a
b
c
A
B
C
练习:
1、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
选一选
2、已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
B
A
B
C
例:在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.
1 m
2 m
A
C
B
D
解:在Rt△ ABC中,∠B=90°,由勾股定理可知:
8
6
算一算
AC2=AB2+BC2=62+82=100
∴AC=√100 = 10
A
B
C
求图中直角三角形的未知边的长度。
解:在Rt△ABC中,根据勾股定理,
练习: 一判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在 ABC中, ∠C=90°,AC=6,CB=8,则
ABC面积为_____,斜边为上的高为______.
24
4.8
A
B
C
D
若a=5,b=12, 则c =___________.
试一试
在Rt△ABC中,
13
当c是斜边时, c2= a2+b2
当b是斜边时, b2= a2+c2
13或√119
1
1
数学的和谐美
勾股定理的命名
2.西方国家称勾股定理为毕达哥拉斯定理.
毕达哥拉斯(Pythagoras,约公元前580~前500年)是古希
腊杰出的数学家,天文学家,哲学家.他不仅提出了定理,
而且努力探求证明方法.
1.约2000年前,我国古代算书《周髀算经》中就记载了公
元前1120年我国古人发现的“勾三股四弦五”.当时把
较短的直角边叫做勾,较长的边叫做股,斜边叫做弦.“
勾三股四弦五”的意思是,在直角三角形中, 如果勾为3,
股为4,那么弦为5.这里3 +4 = 5 .人们还发现, 勾为6,
股为8, 弦一定为10.勾为5,股为12, 弦一定为13等.同
样,有6 +8 =10 ,5 +12 = 13 ,…,即勾 +股 =弦 .所
以,我国称它为勾股定理.
2
2
2
2
2
2
2
2
2
2
2
2
小结
1.勾股定理的内容及证明方法.
2.勾股定理作用:它能把三角形的形的特性(一角为90度)
转化为数量关系,即三边满足:
3.利用勾股定理进行计算要注意利用方程的思想求直角
三角形有关线段的长.
4.适当添加辅助线构建直角三角形使用勾股定理.
作业布置
必做:书 第70页 2、3、5题
选做:书 第71页 阅读与思考
19.1 勾股定理
这就是本届大会会徽的图案.
你见过这个图案吗?
你听说过勾股定理吗?
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
这个图形里蕴涵着怎样博大精深的知识呢?
它标志着我国古代数学的伟大成就!
邮票赏析
这是1955年希腊为纪念一位数学家曾经发行的邮票。
3
4
5
邮票的秘密
观察这枚邮票图案小方格的个数,
你有什么发现
3 +4 =5
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,
相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上
,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看
着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块
直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人
看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥
拉斯恍然大悟的样子,站起来,大笑着跑回家去了.
同学们,我们也来观察下面图中的地面,看看你能
发现什么?是否也和大哲学家有同样的发现呢?
A
B
C
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
B
A
C
图甲 图乙
A的面积
B的面积
C的面积
4
4
8
SA+SB=SC
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
A
B
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
A
B
图乙
2.观察图乙,小方格
的边长为1.
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
a
b
c
a
b
c
C
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
3.猜想a、b、c 之间的关系?
在方格纸上,画
一个顶点都在格点
上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方
形,仿照上面的方法
计算以斜边为一边的正方形的面积.
实验
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
以正方形为基础证明1
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab =c2+2ab
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
a
b
c
证明:
∵ s大正方形=
s大正方形 =
以正方形为基础证明2
c
4× ab+(b-a)
=2ab+b -2ab+b
=a +b
又∵S大正方形=S大正方形
∴c =a +b
a
a
b
b
c
c
∵ s梯形= (a+b)(a+b)= (a2+2ab+b2)
= a2+ab+ b2
s梯形=2× ab+ c2=ab+ c2
∵s梯形=s梯形 ∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
美国第二十任总统伽菲尔德的证法
在数学史上被传为佳话
勾股定理(毕达哥拉斯定理)
(gou-gu theorem)
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于
斜边的平方.
a
c
勾
弦
b
股
结论变形
a2 + b2 = c2
a
b
c
A
B
C
练习:
1、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
选一选
2、已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
B
A
B
C
例:在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.
1 m
2 m
A
C
B
D
解:在Rt△ ABC中,∠B=90°,由勾股定理可知:
8
6
算一算
AC2=AB2+BC2=62+82=100
∴AC=√100 = 10
A
B
C
求图中直角三角形的未知边的长度。
解:在Rt△ABC中,根据勾股定理,
练习: 一判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在 ABC中, ∠C=90°,AC=6,CB=8,则
ABC面积为_____,斜边为上的高为______.
24
4.8
A
B
C
D
若a=5,b=12, 则c =___________.
试一试
在Rt△ABC中,
13
当c是斜边时, c2= a2+b2
当b是斜边时, b2= a2+c2
13或√119
1
1
数学的和谐美
勾股定理的命名
2.西方国家称勾股定理为毕达哥拉斯定理.
毕达哥拉斯(Pythagoras,约公元前580~前500年)是古希
腊杰出的数学家,天文学家,哲学家.他不仅提出了定理,
而且努力探求证明方法.
1.约2000年前,我国古代算书《周髀算经》中就记载了公
元前1120年我国古人发现的“勾三股四弦五”.当时把
较短的直角边叫做勾,较长的边叫做股,斜边叫做弦.“
勾三股四弦五”的意思是,在直角三角形中, 如果勾为3,
股为4,那么弦为5.这里3 +4 = 5 .人们还发现, 勾为6,
股为8, 弦一定为10.勾为5,股为12, 弦一定为13等.同
样,有6 +8 =10 ,5 +12 = 13 ,…,即勾 +股 =弦 .所
以,我国称它为勾股定理.
2
2
2
2
2
2
2
2
2
2
2
2
小结
1.勾股定理的内容及证明方法.
2.勾股定理作用:它能把三角形的形的特性(一角为90度)
转化为数量关系,即三边满足:
3.利用勾股定理进行计算要注意利用方程的思想求直角
三角形有关线段的长.
4.适当添加辅助线构建直角三角形使用勾股定理.
作业布置
必做:书 第70页 2、3、5题
选做:书 第71页 阅读与思考
