教科版_选修3-2_ 第二章 交变电流 _ 1. 交变电流课件38张PPT
文档属性
| 名称 | 教科版_选修3-2_ 第二章 交变电流 _ 1. 交变电流课件38张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-16 00:00:00 | ||
图片预览










文档简介
1 交变电流
第二章 交变电流
[学习目标]
1.会观察电流(或电压)的波形图,理解交变电流和直流的概念.
2.理解交变电流的产生过程,会分析电动势和电流方向的变化规律.
3.知道交变电流的变化规律及表示方法,知道交变电流的瞬时值的物理含义.
内容索引
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
自主预习
预习新知 夯实基础
重点探究
启迪思维 探究重点
达标检测
检测评价 达标过关
自主预习
一、交变电流
1.恒定电流:大小和 都不随时间变化的电流,称为恒定电流.
2.交变电流:大小和方向随时间作 变化的电流,称为交变电流.
3.正弦交变电流:电流随时间按 函数规律变化的交变电流称为____
.
方向
周期性
正弦
正弦
交变电流
二、正弦交变电流的产生和表述
1.正弦交变电流的产生:闭合矩形线圈在 磁场中绕 方向的轴 转动时,线圈中产生的电流是正弦交流电.
2.正弦式交变电流的表述:线圈从 磁场方向计时产生电动势的瞬时值表达式:e=Emsin ωt,Em= .
电路中电流:i= ,外电路两端电压:u= .
匀强
垂直于磁场
匀速
垂直
NBSω
Imsin ωt
Umsin ωt
[即学即用]
1.判断下列说法的正误.
(1)只要线圈在磁场中转动,就可以产生交变电流.( )
(2)线圈在通过中性面时磁通量最大,电流也最大.( )
(3)线圈在通过垂直中性面的平面时电流最大,但磁通量为零.( )
(4)线圈在通过中性面时电流的方向发生改变.( )
答案
×
×
√
√
答案
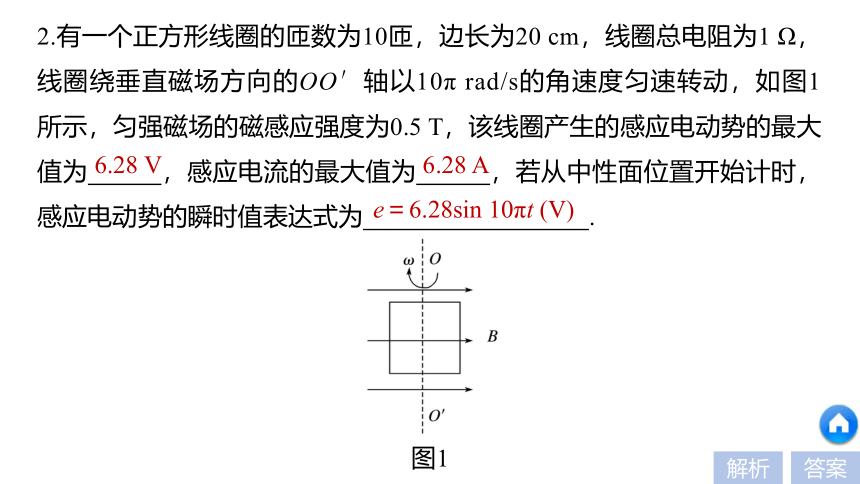
2.有一个正方形线圈的匝数为10匝,边长为20 cm,线圈总电阻为1 Ω,线圈绕垂直磁场方向的OO′轴以10π rad/s的角速度匀速转动,如图1所示,匀强磁场的磁感应强度为0.5 T,该线圈产生的感应电动势的最大值为 ,感应电流的最大值为 ,若从中性面位置开始计时,感应电动势的瞬时值表达式为 .
图1
6.28 V
6.28 A
e=6.28sin 10πt (V)
解析
解析 感应电动势的最大值为Em=nBSω=10×0.5×0.22×10π V=6.28 V
感应电流的最大值为Im= =6.28 A
感应电动势的瞬时值表达式为e=Emsin ωt=6.28sin 10πt (V).
重点探究
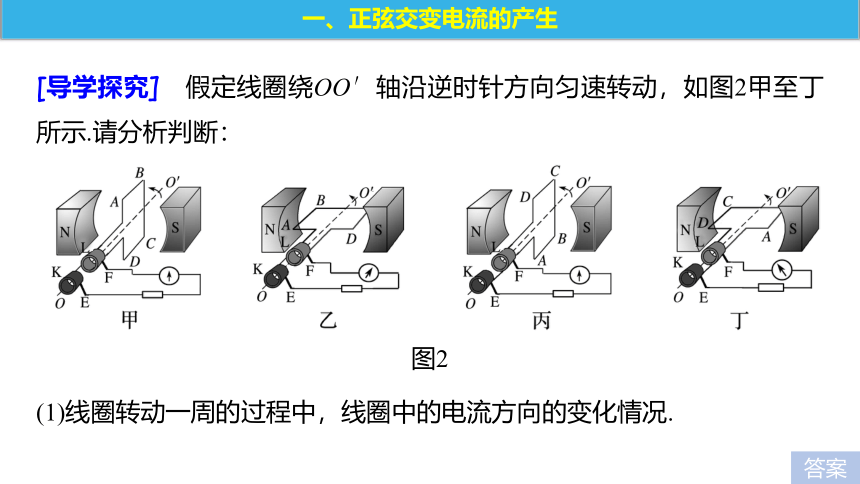
[导学探究] 假定线圈绕OO′轴沿逆时针方向匀速转动,如图2甲至丁所示.请分析判断:
一、正弦交变电流的产生
答案
图2
(1)线圈转动一周的过程中,线圈中的电流方向的变化情况.
答案
转动过程
电流方向
甲→乙
B→A→D→C
乙→丙
B→A→D→C
丙→丁
A→B→C→D
丁→甲
A→B→C→D
(2)线圈转动过程中,当产生的感应电流有最大值和最小值时线圈分别在什么位置?
答案
答案 线圈转到乙或丁位置时线圈中的电流最大.线圈转到甲或丙位置时线圈中电流最小,为零,此时线圈所处的平面称为中性面.
[知识深化] 两个特殊位置
(1)中性面(S⊥B位置,如图2中的甲、丙)
线圈平面与磁场垂直的位置,此时Φ最大, 为0,e为0,i为0.
线圈经过中性面时,电流方向发生改变,线圈转一圈电流方向改变两次.
(2)垂直中性面位置(S∥B位置,如图2中的乙、丁)
此时Φ为0, 最大,e最大,i最大.
例1 (多选)矩形线框绕垂直于匀强磁场且在线框平面内的轴匀速转动时产生了交变电流,下列说法正确的是
A.当线框位于中性面时,线框中感应电动势最大
B.当穿过线框的磁通量为零时,线框中的感应电动势也为零
C.每当线框经过中性面时,感应电动势或感应电流的方向就改变一次
D.线框经过中性面时,各边切割磁感线的速度为零
√
答案
解析
√
解析 线框位于中性面时,线框平面与磁感线垂直,穿过线框的磁通量最大,但此时切割磁感线的两边的速度与磁感线平行,即不切割磁感线,所以感应电动势等于零,此时穿过线框的磁通量的变化率也等于零,感应电动势或感应电流的方向也就在此时刻发生变化.线框垂直于中性面时,穿过线框的磁通量为零,但切割磁感线的两边都垂直切割,有效切割速度最大,所以感应电动势最大,也可以说此时穿过线框的磁通量的变化率最大,故C、D选项正确.
[导学探究] 如图3所示,线圈平面绕bc边的中点从中性面开始转动,角速度为ω.经过时间t,线圈转过的角度是ωt,ab边的线速度v的方向跟磁感线方向间的夹角也等于ωt.设ab边长为L1,bc边长为L2,线圈面积S=L1L2,磁感应强度为B,则:
(1)ab边产生的感应电动势为多大?
答案
二、正弦交变电流的变化规律
图3
答案
(2)整个线圈中的感应电动势为多大?
答案 整个线圈中的感应电动势由ab和cd两边产生的感应电动势组成,且eab=ecd,所以e总=eab+ecd=BSωsin ωt.
(3)若线圈有N匝,则整个线圈的感应电动势为多大?
答案 若线圈有N匝,则相当于N个完全相同的电源串联,所以e=NBSωsin ωt.
[知识深化]
1.最大值表达式
2.最大值决定因素:由线圈匝数N、磁感应强度B、转动角速度ω和线圈面积S决定,与线圈的形状无关,与转轴的位置无关.
如图4所示的几种情况中,
如果N、B、ω、S均相同,
则感应电动势的最大值均
为Em=NBSω.
图4
3.正弦交变电流的瞬时值表达式
(1)从中性面位置开始计时
e=Emsin ωt,i=Imsin ωt,u=Umsin ωt
(2)从与中性面垂直的位置开始计时
e=Emcos ωt,i=Imcos ωt,u=Umcos ωt.
例2 一矩形线圈,面积是0.05 m2,共100匝,线圈电阻r=2 Ω,外接电阻R=8 Ω,线圈在磁感应强度B= T的匀强磁场中以n=300 r/min的转速绕垂直于磁感线的轴匀速转动,如图5所示,若从中性面开始计时,求:
(1)线圈中感应电动势的瞬时值表达式;
图5
答案 e=50sin 10πt (V)
答案
解析
解析 线圈转速n=300 r/min=5 r/s,
角速度ω=2πn=10π rad/s,
线圈产生的感应电动势最大值Em=NBSω=50 V,
由此得到的感应电动势瞬时值表达式为
e=Emsin ωt=50sin 10πt (V).
(2)线圈从开始计时经 s时线圈中由此得到的感应电流的瞬时值;
答案
解析
(3)外电路R两端电压瞬时值的表达式.
答案
解析
答案 u=40sin 10πt (V)
1.求交变电流瞬时值的方法
(1)确定线圈转动从哪个位置开始计时;
(2)确定表达式是正弦函数还是余弦函数;
(3)确定转动的角速度ω=2πn(n的单位为r/s)、最大值Em=NBSω;
(4)写出表达式,代入时间求瞬时值.
方法总结
2.线圈在匀强磁场中绕垂直磁场方向的轴匀速转动产生正弦式交变电流,产生的交变电流与线圈的形状无关.如图6所示,若线圈的面积和匝数与例2题图所示线圈面积相同,则答案完全相同.
图6
如图7甲、乙所示,从图像中可以解读到以下信息:
三、正弦交变电流的图像
图7
(1)交变电流的最大值Em、Im和周期T.
(2)两个特殊值对应的位置:
①e=0(或i=0)时,线圈位于中性面上;
e最大(或i最大)时,线圈平行于磁感线.
②e=0(或i=0)时, =0,Φ最大.
e最大(或i最大)时, 最大,Φ=0.
(3)分析判断e、i大小和方向随时间的变化规律.
例3 一闭合矩形线圈abcd绕垂直于磁感线的固定轴OO′匀速转动,线圈平面位于如图8甲所示的匀强磁场中,通过线圈的磁通量Φ随时间t的变化规律如图乙所示,下列说法正确的是
A.t1、t3时刻通过线圈的磁通量变化率最大
B.t1、t3时刻线圈中感应电流方向改变
C.t2、t4时刻线圈中磁通量最大
D.t2、t4时刻线圈中感应电动势最小
图8
答案
解析
√
解析 由题图乙可知,t1、t3时刻通过线圈的磁通量最大,磁通量的变化率最小,选项A错误;
t1、t3时刻线圈处于中性面上,故此时刻的感应电流方向改变,选项B正确;
t2、t4时刻线圈中磁通量最小,磁通量的变化率最大,感应电动势最大,选项C、D错误.
根据图像找出线圈位于中性面位置时对应的时刻,然后根据中性面的性质进行判断.
总结提升
达标检测
1.(交变电流的产生)(多选)下列各图中,线圈中能产生交变电流的有
答案
√
1
2
3
4
√
√
2.(交变电流的产生及规律)(多选)如图9所示,一矩形闭合线圈在匀强磁场中绕垂直于磁场方向的转轴OO′以恒定的角速度ω转动,从线圈平面与磁场方向平行时开始计时,则在0~ 这段时间内
A.线圈中的感应电流一直在减小
B.线圈中的感应电流先增大后减小
C.穿过线圈的磁通量一直在减小
D.穿过线圈的磁通量的变化率一直在减小
√
答案
图9
1
2
3
4
√
解析
解析 题图所示位置,线圈平面与磁场平行,感应电流最大,因为
在0~ 时间内线圈转过四分之一个周期,感应电流从最大值减小为零,穿过线圈的磁通量逐渐增大,穿过线圈的磁通量的变化率一直在减小,故A、D正确,B、C错误.
1
2
3
4
3.(交变电流的图像)一个矩形线圈在匀强磁场中绕垂直于磁感线的轴匀速转动,穿过线圈的磁通量随时间变化的图像如图10甲所示,则下列说法中正确的是
A.t=0时刻,线圈平面与中性面垂直
B.t=0.01 s时刻,Φ的变化率最大
C.t=0.02 s时刻,感应电动势达到最大
D.该线圈产生的相应感应电动势的图像
如图乙所示
答案
√
图10
解析
1
2
3
4
解析 由题图甲可知t=0时刻,穿过线圈的磁通量最大,线圈处于中性面,t=0.01 s时刻,磁通量为零,但变化率最大,故A项错误,B项正确;
t=0.02 s时刻,感应电动势应为零,故C、D项均错误.
1
2
3
4
4.(交变电流的变化规律)如图11所示,匀强磁场的磁感应强度B= T,边长L=10 cm的正方形线圈abcd共100匝,线圈总电阻r=1 Ω,线圈绕垂直于磁感线的轴OO′匀速转动,角速度ω=2π rad/s,外电路电阻R=4 Ω.求:
(1)转动过程中线圈中感应电动势的最大值.
答案
解析
1
2
3
4
图11
解析 设转动过程中感应电动势的最大值为Em,
(2)从图示位置(线圈平面与磁感线平行)开始感应电动势的瞬时值表达式.
答案
解析
1
2
3
4
解析 从题图所示位置开始感应电动势的瞬时值表达式为e=Emcos ωt=2 cos 2πt (V)
(3)由图示位置转过30°角电路中电流的瞬时值.
解析 从题图所示位置开始转过30°角时感应电动势的瞬时值
第二章 交变电流
[学习目标]
1.会观察电流(或电压)的波形图,理解交变电流和直流的概念.
2.理解交变电流的产生过程,会分析电动势和电流方向的变化规律.
3.知道交变电流的变化规律及表示方法,知道交变电流的瞬时值的物理含义.
内容索引
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
自主预习
预习新知 夯实基础
重点探究
启迪思维 探究重点
达标检测
检测评价 达标过关
自主预习
一、交变电流
1.恒定电流:大小和 都不随时间变化的电流,称为恒定电流.
2.交变电流:大小和方向随时间作 变化的电流,称为交变电流.
3.正弦交变电流:电流随时间按 函数规律变化的交变电流称为____
.
方向
周期性
正弦
正弦
交变电流
二、正弦交变电流的产生和表述
1.正弦交变电流的产生:闭合矩形线圈在 磁场中绕 方向的轴 转动时,线圈中产生的电流是正弦交流电.
2.正弦式交变电流的表述:线圈从 磁场方向计时产生电动势的瞬时值表达式:e=Emsin ωt,Em= .
电路中电流:i= ,外电路两端电压:u= .
匀强
垂直于磁场
匀速
垂直
NBSω
Imsin ωt
Umsin ωt
[即学即用]
1.判断下列说法的正误.
(1)只要线圈在磁场中转动,就可以产生交变电流.( )
(2)线圈在通过中性面时磁通量最大,电流也最大.( )
(3)线圈在通过垂直中性面的平面时电流最大,但磁通量为零.( )
(4)线圈在通过中性面时电流的方向发生改变.( )
答案
×
×
√
√
答案
2.有一个正方形线圈的匝数为10匝,边长为20 cm,线圈总电阻为1 Ω,线圈绕垂直磁场方向的OO′轴以10π rad/s的角速度匀速转动,如图1所示,匀强磁场的磁感应强度为0.5 T,该线圈产生的感应电动势的最大值为 ,感应电流的最大值为 ,若从中性面位置开始计时,感应电动势的瞬时值表达式为 .
图1
6.28 V
6.28 A
e=6.28sin 10πt (V)
解析
解析 感应电动势的最大值为Em=nBSω=10×0.5×0.22×10π V=6.28 V
感应电流的最大值为Im= =6.28 A
感应电动势的瞬时值表达式为e=Emsin ωt=6.28sin 10πt (V).
重点探究
[导学探究] 假定线圈绕OO′轴沿逆时针方向匀速转动,如图2甲至丁所示.请分析判断:
一、正弦交变电流的产生
答案
图2
(1)线圈转动一周的过程中,线圈中的电流方向的变化情况.
答案
转动过程
电流方向
甲→乙
B→A→D→C
乙→丙
B→A→D→C
丙→丁
A→B→C→D
丁→甲
A→B→C→D
(2)线圈转动过程中,当产生的感应电流有最大值和最小值时线圈分别在什么位置?
答案
答案 线圈转到乙或丁位置时线圈中的电流最大.线圈转到甲或丙位置时线圈中电流最小,为零,此时线圈所处的平面称为中性面.
[知识深化] 两个特殊位置
(1)中性面(S⊥B位置,如图2中的甲、丙)
线圈平面与磁场垂直的位置,此时Φ最大, 为0,e为0,i为0.
线圈经过中性面时,电流方向发生改变,线圈转一圈电流方向改变两次.
(2)垂直中性面位置(S∥B位置,如图2中的乙、丁)
此时Φ为0, 最大,e最大,i最大.
例1 (多选)矩形线框绕垂直于匀强磁场且在线框平面内的轴匀速转动时产生了交变电流,下列说法正确的是
A.当线框位于中性面时,线框中感应电动势最大
B.当穿过线框的磁通量为零时,线框中的感应电动势也为零
C.每当线框经过中性面时,感应电动势或感应电流的方向就改变一次
D.线框经过中性面时,各边切割磁感线的速度为零
√
答案
解析
√
解析 线框位于中性面时,线框平面与磁感线垂直,穿过线框的磁通量最大,但此时切割磁感线的两边的速度与磁感线平行,即不切割磁感线,所以感应电动势等于零,此时穿过线框的磁通量的变化率也等于零,感应电动势或感应电流的方向也就在此时刻发生变化.线框垂直于中性面时,穿过线框的磁通量为零,但切割磁感线的两边都垂直切割,有效切割速度最大,所以感应电动势最大,也可以说此时穿过线框的磁通量的变化率最大,故C、D选项正确.
[导学探究] 如图3所示,线圈平面绕bc边的中点从中性面开始转动,角速度为ω.经过时间t,线圈转过的角度是ωt,ab边的线速度v的方向跟磁感线方向间的夹角也等于ωt.设ab边长为L1,bc边长为L2,线圈面积S=L1L2,磁感应强度为B,则:
(1)ab边产生的感应电动势为多大?
答案
二、正弦交变电流的变化规律
图3
答案
(2)整个线圈中的感应电动势为多大?
答案 整个线圈中的感应电动势由ab和cd两边产生的感应电动势组成,且eab=ecd,所以e总=eab+ecd=BSωsin ωt.
(3)若线圈有N匝,则整个线圈的感应电动势为多大?
答案 若线圈有N匝,则相当于N个完全相同的电源串联,所以e=NBSωsin ωt.
[知识深化]
1.最大值表达式
2.最大值决定因素:由线圈匝数N、磁感应强度B、转动角速度ω和线圈面积S决定,与线圈的形状无关,与转轴的位置无关.
如图4所示的几种情况中,
如果N、B、ω、S均相同,
则感应电动势的最大值均
为Em=NBSω.
图4
3.正弦交变电流的瞬时值表达式
(1)从中性面位置开始计时
e=Emsin ωt,i=Imsin ωt,u=Umsin ωt
(2)从与中性面垂直的位置开始计时
e=Emcos ωt,i=Imcos ωt,u=Umcos ωt.
例2 一矩形线圈,面积是0.05 m2,共100匝,线圈电阻r=2 Ω,外接电阻R=8 Ω,线圈在磁感应强度B= T的匀强磁场中以n=300 r/min的转速绕垂直于磁感线的轴匀速转动,如图5所示,若从中性面开始计时,求:
(1)线圈中感应电动势的瞬时值表达式;
图5
答案 e=50sin 10πt (V)
答案
解析
解析 线圈转速n=300 r/min=5 r/s,
角速度ω=2πn=10π rad/s,
线圈产生的感应电动势最大值Em=NBSω=50 V,
由此得到的感应电动势瞬时值表达式为
e=Emsin ωt=50sin 10πt (V).
(2)线圈从开始计时经 s时线圈中由此得到的感应电流的瞬时值;
答案
解析
(3)外电路R两端电压瞬时值的表达式.
答案
解析
答案 u=40sin 10πt (V)
1.求交变电流瞬时值的方法
(1)确定线圈转动从哪个位置开始计时;
(2)确定表达式是正弦函数还是余弦函数;
(3)确定转动的角速度ω=2πn(n的单位为r/s)、最大值Em=NBSω;
(4)写出表达式,代入时间求瞬时值.
方法总结
2.线圈在匀强磁场中绕垂直磁场方向的轴匀速转动产生正弦式交变电流,产生的交变电流与线圈的形状无关.如图6所示,若线圈的面积和匝数与例2题图所示线圈面积相同,则答案完全相同.
图6
如图7甲、乙所示,从图像中可以解读到以下信息:
三、正弦交变电流的图像
图7
(1)交变电流的最大值Em、Im和周期T.
(2)两个特殊值对应的位置:
①e=0(或i=0)时,线圈位于中性面上;
e最大(或i最大)时,线圈平行于磁感线.
②e=0(或i=0)时, =0,Φ最大.
e最大(或i最大)时, 最大,Φ=0.
(3)分析判断e、i大小和方向随时间的变化规律.
例3 一闭合矩形线圈abcd绕垂直于磁感线的固定轴OO′匀速转动,线圈平面位于如图8甲所示的匀强磁场中,通过线圈的磁通量Φ随时间t的变化规律如图乙所示,下列说法正确的是
A.t1、t3时刻通过线圈的磁通量变化率最大
B.t1、t3时刻线圈中感应电流方向改变
C.t2、t4时刻线圈中磁通量最大
D.t2、t4时刻线圈中感应电动势最小
图8
答案
解析
√
解析 由题图乙可知,t1、t3时刻通过线圈的磁通量最大,磁通量的变化率最小,选项A错误;
t1、t3时刻线圈处于中性面上,故此时刻的感应电流方向改变,选项B正确;
t2、t4时刻线圈中磁通量最小,磁通量的变化率最大,感应电动势最大,选项C、D错误.
根据图像找出线圈位于中性面位置时对应的时刻,然后根据中性面的性质进行判断.
总结提升
达标检测
1.(交变电流的产生)(多选)下列各图中,线圈中能产生交变电流的有
答案
√
1
2
3
4
√
√
2.(交变电流的产生及规律)(多选)如图9所示,一矩形闭合线圈在匀强磁场中绕垂直于磁场方向的转轴OO′以恒定的角速度ω转动,从线圈平面与磁场方向平行时开始计时,则在0~ 这段时间内
A.线圈中的感应电流一直在减小
B.线圈中的感应电流先增大后减小
C.穿过线圈的磁通量一直在减小
D.穿过线圈的磁通量的变化率一直在减小
√
答案
图9
1
2
3
4
√
解析
解析 题图所示位置,线圈平面与磁场平行,感应电流最大,因为
在0~ 时间内线圈转过四分之一个周期,感应电流从最大值减小为零,穿过线圈的磁通量逐渐增大,穿过线圈的磁通量的变化率一直在减小,故A、D正确,B、C错误.
1
2
3
4
3.(交变电流的图像)一个矩形线圈在匀强磁场中绕垂直于磁感线的轴匀速转动,穿过线圈的磁通量随时间变化的图像如图10甲所示,则下列说法中正确的是
A.t=0时刻,线圈平面与中性面垂直
B.t=0.01 s时刻,Φ的变化率最大
C.t=0.02 s时刻,感应电动势达到最大
D.该线圈产生的相应感应电动势的图像
如图乙所示
答案
√
图10
解析
1
2
3
4
解析 由题图甲可知t=0时刻,穿过线圈的磁通量最大,线圈处于中性面,t=0.01 s时刻,磁通量为零,但变化率最大,故A项错误,B项正确;
t=0.02 s时刻,感应电动势应为零,故C、D项均错误.
1
2
3
4
4.(交变电流的变化规律)如图11所示,匀强磁场的磁感应强度B= T,边长L=10 cm的正方形线圈abcd共100匝,线圈总电阻r=1 Ω,线圈绕垂直于磁感线的轴OO′匀速转动,角速度ω=2π rad/s,外电路电阻R=4 Ω.求:
(1)转动过程中线圈中感应电动势的最大值.
答案
解析
1
2
3
4
图11
解析 设转动过程中感应电动势的最大值为Em,
(2)从图示位置(线圈平面与磁感线平行)开始感应电动势的瞬时值表达式.
答案
解析
1
2
3
4
解析 从题图所示位置开始感应电动势的瞬时值表达式为e=Emcos ωt=2 cos 2πt (V)
(3)由图示位置转过30°角电路中电流的瞬时值.
解析 从题图所示位置开始转过30°角时感应电动势的瞬时值
