22.2 二次函数与一元二次方程 高频易错题集 (原卷+解析)
文档属性
| 名称 | 22.2 二次函数与一元二次方程 高频易错题集 (原卷+解析) |  | |
| 格式 | zip | ||
| 文件大小 | 616.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 09:49:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
22.2
二次函数与一元二次方程
高频易错题集
一.选择题(共10小题)
1.如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0
B.﹣
C.2
D.﹣2
2.若二次函数y=x2﹣2x+c的图象与坐标轴只有两个公共点,则c应满足的条件是( )
A.c=0
B.c=1
C.c=0或c=1
D.c=0或c=﹣1
3.将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A.﹣或﹣12
B.﹣或2
C.﹣12或2
D.﹣或﹣12
4.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
y=ax2+bx+c
…
t
m
﹣2
﹣2
n
…
且当x=﹣时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<,其中,正确结论的是( )
A.①②③
B.①②
C.①③
D.②③
5.抛物线y=x2﹣2x﹣1的图象与x轴交点有( )
A.两个交点
B.一个交点
C.无交点
D.无法确定
6.如图,抛物线y=﹣x2+x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
A.2
B.3
C.5
D.+
7.如图一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,如此进行下去,直至得到C10,若点P(28,m)在第10段抛物线C10上,则m的值为( )
A.1
B.﹣1
C.2
D.﹣2
8.如图,一条抛物线与x轴相交于A
(x1,0)、B(x2,0)两点(点B在点A的右侧),其顶点P在线段MN上移动.M、N的坐标分别为(﹣1,2)、(1,2).x1的最小值为﹣3,则x2的最大值为( )
A.﹣1
B.1
C.3
D.5
9.若抛物线y=x2﹣(m﹣3)x﹣m能与x轴交,则两交点间的距离最值是( )
A.最大值2
B.最小值2
C.最大值2
D.最小值2
10.关于函数y=x2+2x﹣3的叙述:
①当x>1时,y的值随x的增大而增大;
②y的最小值是﹣3;
③函数图象与x轴交点的横坐标是方程x2+2x﹣3=0的根;
④函数图象与y轴交点的坐标是(0,﹣3);
⑤函数图象不经过第四象限.
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
二.填空题(共5小题)
11.抛物线y=9x2﹣px+4与x轴只有一个公共点,则p的值是
.
12.如图,在平面直角坐标系中,O为坐标原点,抛物线y=x2﹣2x与x轴正半轴交于点A,点B的坐标为(0,3).C是该抛物线第一象限图象上的一点,A,B,C三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点C的横坐标为m,若这个正方形的面积最小,则m的取值范围是
.
13.如图,抛物线y1的顶点在y轴上,y2由y1平移得到,它们与x轴的交点为A、B、C,且2BC=3AB=4OD=6,若过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为
.
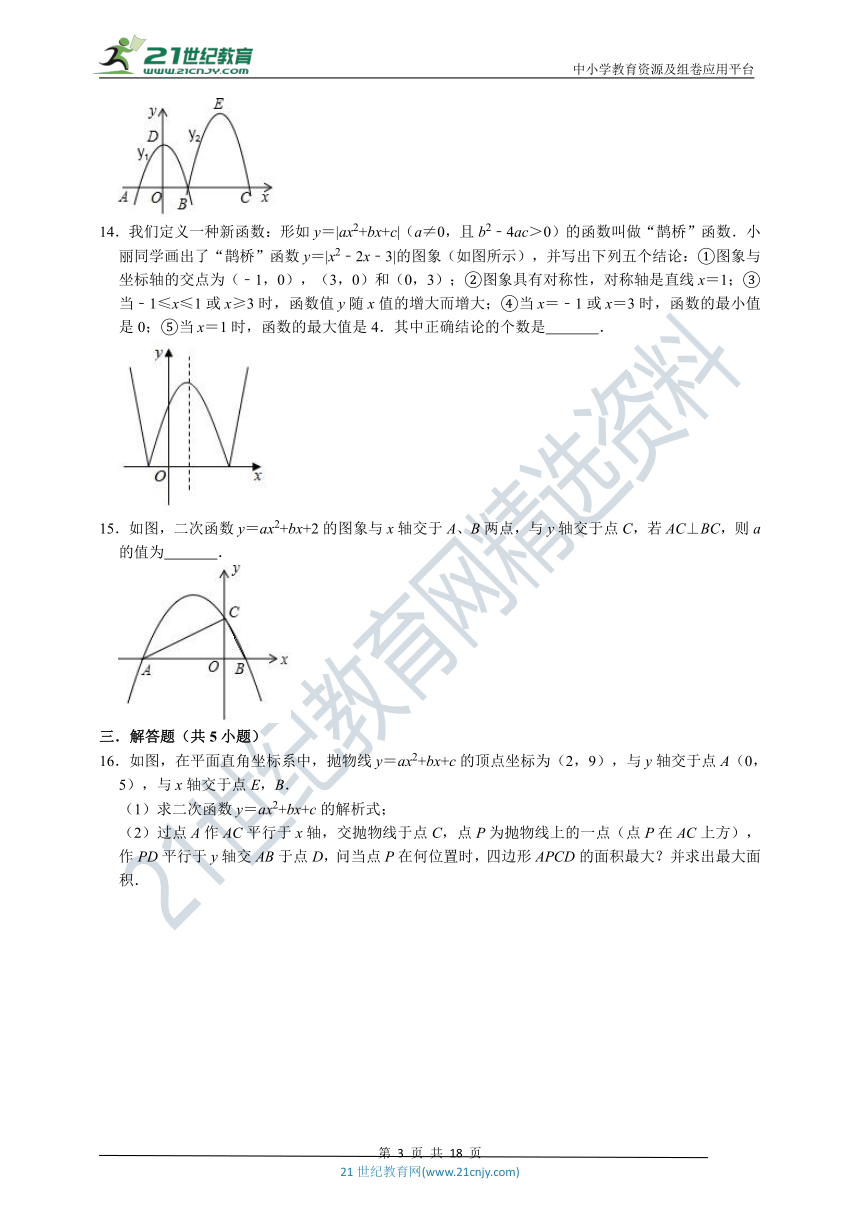
14.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是
.
15.如图,二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于点C,若AC⊥BC,则a的值为
.
三.解答题(共5小题)
16.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
17.已知k是常数,抛物线y=x2+(k2+k﹣6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在物线y=x2+(k2+k﹣6)x+3k上,且P到y轴的距离是2,求点P的坐标.
18.在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx﹣,经过点A(﹣1,0)、B(5,0).
(1)求此抛物线顶点C的坐标;
(2)联结AC交y轴于点D,联结BD、BC,过点C作CH⊥BD,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
19.求出y=2(x﹣1)2﹣8与坐标轴的交点坐标,直接写出y>0时x的取值范围.
20.利用二次函数的图象,求下列一元二次方程的近似根.
(1)x2+11x=9;
(2)x2+3x+2=0;
(3)x2+2x﹣9=0;
(4)x2+3=3x.
试题解析
一.选择题(共10小题)
1.如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0
B.﹣
C.2
D.﹣2
解:当y=0时,x2﹣3x=0,
解得:x1=0,x2=3,
∴点A1的坐标为(3,0).
由旋转的性质,可知:点A2的坐标为(6,0).
∵2020=336×6+4,
∴当x=4时,y=m.
由图象可知:当x=2时的y值与当x=4时的y值互为相反数,
∴m=﹣(2×2﹣3×2)=2.
故选:C.
2.若二次函数y=x2﹣2x+c的图象与坐标轴只有两个公共点,则c应满足的条件是( )
A.c=0
B.c=1
C.c=0或c=1
D.c=0或c=﹣1
解:∵二次函数y=x2﹣2x+c的图象与坐标轴只有两个公共点,
∴二次函数y=x2﹣2x+c的图象与x轴只有一个公共点或者与x轴有两个公共点,其中一个为原点,
当二次函数y=x2﹣2x+c的图象与x轴只有一个公共点时,
(﹣2)2﹣4×1×c=0,得c=1;
当二次函数y=x2﹣2x+c的图象与x轴有两个公共点,其中一个为原点时,
则c=0,y=x2﹣2x=x(x﹣2),与x轴两个交点,坐标分别为(0,0),(2,0);
由上可得,c的值是1或0,
故选:C.
3.将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A.﹣或﹣12
B.﹣或2
C.﹣12或2
D.﹣或﹣12
解:如图所示,过点B的直线y=2x+b与新图象有三个公共点,将直线向下平移到恰在点C处相切,此时与新图象也有三个公共点,
令y=x2﹣5x﹣6=0,解得:x=﹣1或6,即点B坐标(6,0),
将一次函数与二次函数表达式联立得:x2﹣5x﹣6=2x+b,整理得:x2﹣7x﹣6﹣b=0,
△=49﹣4(﹣6﹣b)=0,解得:b=﹣,
当一次函数过点B时,将点B坐标代入:y=2x+b得:0=12+b,解得:b=﹣12,
综上,直线y=2x+b与这个新图象有3个公共点,则b的值为﹣12或﹣;
故选:A.
4.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
y=ax2+bx+c
…
t
m
﹣2
﹣2
n
…
且当x=﹣时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<,其中,正确结论的是( )
A.①②③
B.①②
C.①③
D.②③
解:①根据图表可知:
二次函数y=ax2+bx+c的图象过点(0,﹣2),(1,﹣2),
∴对称轴为直线x==,c=﹣2,
∴a>0,b<0,
∴函数图象的顶点在第四象限内;
①正确;
②根据二次函数的对称性可知:
(﹣2,t)关于对称轴x=的对称点为(3,t),
即﹣2和3是关于x的方程ax2+bx+c=t的两个根,
∴②正确;
③∵对称轴为直线x=,∴﹣=,∴b=﹣a,
∵当x=﹣时,与其对应的函数值y>0,
∴a﹣b﹣2>0,即a+a﹣2>0,∴a>.
∵对称轴为直线x=,二次函数y=ax2+bx+c的图象过点(﹣1,m)(2,n),
∴m=n,当x=﹣1时,m=a﹣b+c=a+a﹣2=2a﹣2,
∴m+n=4a﹣4,∵a>.
∴4a﹣4>,
∴③错误.
故选:B.
5.抛物线y=x2﹣2x﹣1的图象与x轴交点有( )
A.两个交点
B.一个交点
C.无交点
D.无法确定
解:∵△=b2﹣4ac=(﹣2)2﹣4×1×(﹣1)=8>0,
∴二次函数y=x2﹣2x﹣1的图象与x轴有2个交点,
故选:A.
6.如图,抛物线y=﹣x2+x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
A.2
B.3
C.5
D.+
解:作点C关于直线l的对称点C′,连接AC′交直线l于P,连接PC,
则△APC的周长的最小,
由抛物线的对称性可知,点C′在抛物线上,
当x=0时,y=2,
∴点C的坐标为(0,2),
∴点C′的纵坐标为2,
2=﹣x2+x+2,
解得,x1=0,x2=3,
则点C′的横坐标为3,
﹣x2+x+2=0,
x1=﹣1,x2=4,
则点A的坐标为(﹣1,0),
∴AC′==2,AC==,
∴△APC的周长的最小值是3,
故选:B.
7.如图一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,如此进行下去,直至得到C10,若点P(28,m)在第10段抛物线C10上,则m的值为( )
A.1
B.﹣1
C.2
D.﹣2
解:令y=0,则﹣x(x﹣3)=0,
解得x1=0,x2=3,
∴A1(3,0),
由图可知,抛物线C10在x轴下方,
相当于抛物线C1向右平移3×9=27个单位,再沿x轴翻折得到,
∴抛物线C10的解析式为y=(x﹣27)(x﹣27﹣3)=(x﹣27)(x﹣30),
∵P(28,m)在第10段抛物线C10上,
∴m=(28﹣27)(28﹣30)=﹣2.
故选:D.
8.如图,一条抛物线与x轴相交于A
(x1,0)、B(x2,0)两点(点B在点A的右侧),其顶点P在线段MN上移动.M、N的坐标分别为(﹣1,2)、(1,2).x1的最小值为﹣3,则x2的最大值为( )
A.﹣1
B.1
C.3
D.5
解:抛物线顶点平移到点M时,由已知x1的最小值为﹣3
则设此时抛物线解析式为:y=a(x+1)2+2
把(﹣3,0)代入得
a=﹣
则当抛物线顶点平移到N时,解析式为y=﹣(x﹣1)2+2.
当y=0时,解得抛物线与x轴交点坐标为(3,0)或(﹣1,0)
则x2的最大值为3.
故选:C.
9.若抛物线y=x2﹣(m﹣3)x﹣m能与x轴交,则两交点间的距离最值是( )
A.最大值2
B.最小值2
C.最大值2
D.最小值2
解:设x1,x2是方程x2﹣(m﹣3)x﹣m=0的两根,抛物线y=x2﹣(m﹣3)x﹣m与x轴的交点为A、B,
∴x1+x2=m﹣3,x1?x2=﹣m.
∵两交点间的距离AB=|x1﹣x2|,
∴AB2=(x1﹣x2)2
=(x1+x2)2﹣4x1x2
=(m﹣3)2﹣4(﹣m)
=(m﹣1)2+8,
∴当m=1时,AB2有最小值8,
∴AB有最小值,即AB==2,
故选:D.
10.关于函数y=x2+2x﹣3的叙述:
①当x>1时,y的值随x的增大而增大;
②y的最小值是﹣3;
③函数图象与x轴交点的横坐标是方程x2+2x﹣3=0的根;
④函数图象与y轴交点的坐标是(0,﹣3);
⑤函数图象不经过第四象限.
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
解:①抛物线开口向上,对称轴为直线x=﹣1,故当x>1时,y的值随x的增大而增大,正确;
②y的最小值是=﹣4,错误;
③函数图象与x轴交点的横坐标是方程x2+2x﹣3=0的根,正确;
④令x=0,则y=﹣3,故函数图象与y轴交点的坐标是(0,﹣3),正确;
⑤函数图象经过四个象限,错误.
故选:B.
二.填空题(共5小题)
11.抛物线y=9x2﹣px+4与x轴只有一个公共点,则p的值是 ±12 .
解:根据题意:p2﹣4×9×4=0,
解得p=±12.
12.如图,在平面直角坐标系中,O为坐标原点,抛物线y=x2﹣2x与x轴正半轴交于点A,点B的坐标为(0,3).C是该抛物线第一象限图象上的一点,A,B,C三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点C的横坐标为m,若这个正方形的面积最小,则m的取值范围是 2<m≤3. .
解:∵抛物线y=x2﹣2x与x轴正半轴交于点A,
∴点A的坐标为(2,0),
如图所示:
当A,B,C三点均在某一个正方形的边上,
且该正方形的任何一条边均与某条坐标轴平行,
∵点B的坐标为(0,3),
正方形的面积最小时,
此时正方形的边长为3,
∴过点A、B、C的正方形的面积最小值为9,
∴S≥9.
当y=3时,
x2﹣2x=3,
解得x1=﹣1,x2=3,
∴当2<m≤3,时,
正方形面积有最小值;
当m=﹣1时,
正方形最小边长也为3,
正方形面积也有最小值,
∵C在第一象限,m>0,
综上所述:点C的横坐标m的取值范围是:
2<m≤3.
故答案为:2<m≤3.
13.如图,抛物线y1的顶点在y轴上,y2由y1平移得到,它们与x轴的交点为A、B、C,且2BC=3AB=4OD=6,若过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为 y=x .
解:解法一::∵2BC=3AB=4OD=6,
∴BC=3,AB=2,OD=,
则:A(﹣1,0)、B(1,0)、D(0,)、C(4,0),
把A(﹣1,0)、B(1,0)、D(0,)三点坐标代入:y=ax2+bx+c,
解得:y1=﹣x2+,顶点D(0,),
同理可得:y2=﹣x2+x﹣6=﹣(x﹣)2+,顶点E(,),
由平移可知:y1向右平移了个单位,再向上平移了个单位,得到y2,
所以过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线一定经过点(,),
设过原点的直线方程为:y=kx,(k>0),
则k=,
∴k=,
故:直线的解析式为y=x.
解法二:∵2BC=3AB=4OD=6,
∴BC=3,AB=2,OD=,
则:A(﹣1,0)、B(1,0)、D(0,)、C(4,0),
把A(﹣1,0)、B(1,0)、D(0,)三点坐标代入:y=ax2+bx+c,
解得:y1=﹣x2+…①,
同理可得:y2=﹣x2+x﹣6…②;
设:过原点的直线方程为:y=kx,(k>0)…③,
联立①、③得:3x2+2kx﹣3=0,
则:x1+x2=﹣,x1x2=﹣1,
则:G、F两点横坐标差=x2﹣x1===,
同理:K、H两点横坐标差=,
∵AG=KH,
∴=,
解得:k=,
故:直线的解析式为y=x.
14.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是 4 .
解:①∵(﹣1,0),(3,0)和(0,3)坐标都满足函数y=|x2﹣2x﹣3|,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线x=1,因此②也是正确的;
③根据函数的图象和性质,发现当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大,因此③也是正确的;
④函数图象的最低点就是与x轴的两个交点,根据y=0,求出相应的x的值为x=﹣1或x=3,因此④也是正确的;
⑤从图象上看,当x<﹣1或x>3,函数值要大于当x=1时的y=|x2﹣2x﹣3|=4,因此⑤是不正确的;
故答案是:4
15.如图,二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于点C,若AC⊥BC,则a的值为 .
解:∵∠ACB=90°,CO⊥AB,根据射影定理可得CO2=AO×BO.
根据抛物线的解析式可知OC=2,设A(m,0),B(n,0),则m和n是方程ax2+bx+2=0的两个根,
所以mn=.
∴22=﹣mn=﹣,解得a=﹣.
故答案为﹣
三.解答题(共5小题)
16.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5,
(2)当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD=×AC×PD=2(﹣x2+5x)=﹣2x2+10x=﹣2(x﹣)2+,
∵﹣2<0
∴当x=时,
∴即:点P(,)时,S四边形APCD最大=.
17.已知k是常数,抛物线y=x2+(k2+k﹣6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在物线y=x2+(k2+k﹣6)x+3k上,且P到y轴的距离是2,求点P的坐标.
解:(1)∵抛物线y=x2+(k2+k﹣6)x+3k的对称轴是y轴,
∴k2+k﹣6=0,解得k1=﹣3,k2=2;
又∵抛物线y=x2+(k2+k﹣6)x+3k与x轴有两个交点.
∴3k<0
∴k=﹣3.此时抛物线的关系式为y=x2﹣9,
因此k的值为﹣3.
(2)∵点P在抛物线y=x2﹣9上,且P到y轴的距离是2,
∴点P的横坐标为2或﹣2,
当x=2时,y=﹣5
当x=﹣2时,y=﹣5.
∴P(2,﹣5)或P(﹣2,﹣5)
因此点P的坐标为:P(2,﹣5)或P(﹣2,﹣5).
18.在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx﹣,经过点A(﹣1,0)、B(5,0).
(1)求此抛物线顶点C的坐标;
(2)联结AC交y轴于点D,联结BD、BC,过点C作CH⊥BD,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
解:(1)把A(﹣1,0)、B(5,0)代入抛物线解析式,
得:,解得:,
∴抛物线的解析式为:,
∴顶点C(2,﹣3)
(2)方法一:设BD与CG相交于点P,
设直线AC的解析式为:y=kx+b
把A(﹣1,0)和C(2,﹣3)代入得:
解得:
则直线AC:y=﹣x﹣1,
∴D(0,﹣1),
同理可得直线BD:y=x﹣1,
∴
∵∠CHP=∠PGB=90°,∠GPB=∠CPH
∴△BPG∽△CPH,
∴
∴△HPG∽△CPB,
∴,
∴,
∴;
方法二:如图2,过点H作HM⊥CG于M,
∵,,,
∴BD2=CD2+BC2,
∴∠BCD=90°,
∵S△BCD=BD?CH=BC?CD,
∴,
∵∠ABD=∠HCG,
∴△OBD∽△MCH,
∴,
∴,,
∴,
由勾股定理得:GH=
∴,
方法三:直线AC:y=﹣x﹣1,
∴D(0,﹣1),
直线BD:y=x﹣1,
∵CH⊥BD,
∴kBD?kCH=﹣1,
∴直线CH:y=﹣5x+7,
联立解析式:,解得:,
∴H(,﹣),
∴.
19.求出y=2(x﹣1)2﹣8与坐标轴的交点坐标,直接写出y>0时x的取值范围.
解:y=2(x﹣1)2﹣8,
令x=0,则y=﹣6;
令y=0,则0=2(x﹣1)2﹣8,
解得x=3,或x=﹣1,
∴抛物线与y轴交于(0,﹣6),与x轴交于(3,0)或(﹣1,0),
当y>0时,x的取值范围为x>3或x<﹣1.
20.利用二次函数的图象,求下列一元二次方程的近似根.
(1)x2+11x=9;
(2)x2+3x+2=0;
(3)x2+2x﹣9=0;
(4)x2+3=3x.
解:(1)如图1:
方程的近似根为x1≈0.8,x2≈﹣11.8;
(2)如图2:
方程的根为x1=﹣1.0,x2=﹣2.0;
(3)如图3:
方程的近似根为x1≈﹣4.2,x2≈2.2;
(4)如图4:
方程没有实数解.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
22.2
二次函数与一元二次方程
高频易错题集
一.选择题(共10小题)
1.如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0
B.﹣
C.2
D.﹣2
2.若二次函数y=x2﹣2x+c的图象与坐标轴只有两个公共点,则c应满足的条件是( )
A.c=0
B.c=1
C.c=0或c=1
D.c=0或c=﹣1
3.将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A.﹣或﹣12
B.﹣或2
C.﹣12或2
D.﹣或﹣12
4.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
y=ax2+bx+c
…
t
m
﹣2
﹣2
n
…
且当x=﹣时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<,其中,正确结论的是( )
A.①②③
B.①②
C.①③
D.②③
5.抛物线y=x2﹣2x﹣1的图象与x轴交点有( )
A.两个交点
B.一个交点
C.无交点
D.无法确定
6.如图,抛物线y=﹣x2+x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
A.2
B.3
C.5
D.+
7.如图一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,如此进行下去,直至得到C10,若点P(28,m)在第10段抛物线C10上,则m的值为( )
A.1
B.﹣1
C.2
D.﹣2
8.如图,一条抛物线与x轴相交于A
(x1,0)、B(x2,0)两点(点B在点A的右侧),其顶点P在线段MN上移动.M、N的坐标分别为(﹣1,2)、(1,2).x1的最小值为﹣3,则x2的最大值为( )
A.﹣1
B.1
C.3
D.5
9.若抛物线y=x2﹣(m﹣3)x﹣m能与x轴交,则两交点间的距离最值是( )
A.最大值2
B.最小值2
C.最大值2
D.最小值2
10.关于函数y=x2+2x﹣3的叙述:
①当x>1时,y的值随x的增大而增大;
②y的最小值是﹣3;
③函数图象与x轴交点的横坐标是方程x2+2x﹣3=0的根;
④函数图象与y轴交点的坐标是(0,﹣3);
⑤函数图象不经过第四象限.
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
二.填空题(共5小题)
11.抛物线y=9x2﹣px+4与x轴只有一个公共点,则p的值是
.
12.如图,在平面直角坐标系中,O为坐标原点,抛物线y=x2﹣2x与x轴正半轴交于点A,点B的坐标为(0,3).C是该抛物线第一象限图象上的一点,A,B,C三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点C的横坐标为m,若这个正方形的面积最小,则m的取值范围是
.
13.如图,抛物线y1的顶点在y轴上,y2由y1平移得到,它们与x轴的交点为A、B、C,且2BC=3AB=4OD=6,若过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为
.
14.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是
.
15.如图,二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于点C,若AC⊥BC,则a的值为
.
三.解答题(共5小题)
16.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
17.已知k是常数,抛物线y=x2+(k2+k﹣6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在物线y=x2+(k2+k﹣6)x+3k上,且P到y轴的距离是2,求点P的坐标.
18.在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx﹣,经过点A(﹣1,0)、B(5,0).
(1)求此抛物线顶点C的坐标;
(2)联结AC交y轴于点D,联结BD、BC,过点C作CH⊥BD,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
19.求出y=2(x﹣1)2﹣8与坐标轴的交点坐标,直接写出y>0时x的取值范围.
20.利用二次函数的图象,求下列一元二次方程的近似根.
(1)x2+11x=9;
(2)x2+3x+2=0;
(3)x2+2x﹣9=0;
(4)x2+3=3x.
试题解析
一.选择题(共10小题)
1.如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0
B.﹣
C.2
D.﹣2
解:当y=0时,x2﹣3x=0,
解得:x1=0,x2=3,
∴点A1的坐标为(3,0).
由旋转的性质,可知:点A2的坐标为(6,0).
∵2020=336×6+4,
∴当x=4时,y=m.
由图象可知:当x=2时的y值与当x=4时的y值互为相反数,
∴m=﹣(2×2﹣3×2)=2.
故选:C.
2.若二次函数y=x2﹣2x+c的图象与坐标轴只有两个公共点,则c应满足的条件是( )
A.c=0
B.c=1
C.c=0或c=1
D.c=0或c=﹣1
解:∵二次函数y=x2﹣2x+c的图象与坐标轴只有两个公共点,
∴二次函数y=x2﹣2x+c的图象与x轴只有一个公共点或者与x轴有两个公共点,其中一个为原点,
当二次函数y=x2﹣2x+c的图象与x轴只有一个公共点时,
(﹣2)2﹣4×1×c=0,得c=1;
当二次函数y=x2﹣2x+c的图象与x轴有两个公共点,其中一个为原点时,
则c=0,y=x2﹣2x=x(x﹣2),与x轴两个交点,坐标分别为(0,0),(2,0);
由上可得,c的值是1或0,
故选:C.
3.将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A.﹣或﹣12
B.﹣或2
C.﹣12或2
D.﹣或﹣12
解:如图所示,过点B的直线y=2x+b与新图象有三个公共点,将直线向下平移到恰在点C处相切,此时与新图象也有三个公共点,
令y=x2﹣5x﹣6=0,解得:x=﹣1或6,即点B坐标(6,0),
将一次函数与二次函数表达式联立得:x2﹣5x﹣6=2x+b,整理得:x2﹣7x﹣6﹣b=0,
△=49﹣4(﹣6﹣b)=0,解得:b=﹣,
当一次函数过点B时,将点B坐标代入:y=2x+b得:0=12+b,解得:b=﹣12,
综上,直线y=2x+b与这个新图象有3个公共点,则b的值为﹣12或﹣;
故选:A.
4.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
y=ax2+bx+c
…
t
m
﹣2
﹣2
n
…
且当x=﹣时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<,其中,正确结论的是( )
A.①②③
B.①②
C.①③
D.②③
解:①根据图表可知:
二次函数y=ax2+bx+c的图象过点(0,﹣2),(1,﹣2),
∴对称轴为直线x==,c=﹣2,
∴a>0,b<0,
∴函数图象的顶点在第四象限内;
①正确;
②根据二次函数的对称性可知:
(﹣2,t)关于对称轴x=的对称点为(3,t),
即﹣2和3是关于x的方程ax2+bx+c=t的两个根,
∴②正确;
③∵对称轴为直线x=,∴﹣=,∴b=﹣a,
∵当x=﹣时,与其对应的函数值y>0,
∴a﹣b﹣2>0,即a+a﹣2>0,∴a>.
∵对称轴为直线x=,二次函数y=ax2+bx+c的图象过点(﹣1,m)(2,n),
∴m=n,当x=﹣1时,m=a﹣b+c=a+a﹣2=2a﹣2,
∴m+n=4a﹣4,∵a>.
∴4a﹣4>,
∴③错误.
故选:B.
5.抛物线y=x2﹣2x﹣1的图象与x轴交点有( )
A.两个交点
B.一个交点
C.无交点
D.无法确定
解:∵△=b2﹣4ac=(﹣2)2﹣4×1×(﹣1)=8>0,
∴二次函数y=x2﹣2x﹣1的图象与x轴有2个交点,
故选:A.
6.如图,抛物线y=﹣x2+x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
A.2
B.3
C.5
D.+
解:作点C关于直线l的对称点C′,连接AC′交直线l于P,连接PC,
则△APC的周长的最小,
由抛物线的对称性可知,点C′在抛物线上,
当x=0时,y=2,
∴点C的坐标为(0,2),
∴点C′的纵坐标为2,
2=﹣x2+x+2,
解得,x1=0,x2=3,
则点C′的横坐标为3,
﹣x2+x+2=0,
x1=﹣1,x2=4,
则点A的坐标为(﹣1,0),
∴AC′==2,AC==,
∴△APC的周长的最小值是3,
故选:B.
7.如图一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,如此进行下去,直至得到C10,若点P(28,m)在第10段抛物线C10上,则m的值为( )
A.1
B.﹣1
C.2
D.﹣2
解:令y=0,则﹣x(x﹣3)=0,
解得x1=0,x2=3,
∴A1(3,0),
由图可知,抛物线C10在x轴下方,
相当于抛物线C1向右平移3×9=27个单位,再沿x轴翻折得到,
∴抛物线C10的解析式为y=(x﹣27)(x﹣27﹣3)=(x﹣27)(x﹣30),
∵P(28,m)在第10段抛物线C10上,
∴m=(28﹣27)(28﹣30)=﹣2.
故选:D.
8.如图,一条抛物线与x轴相交于A
(x1,0)、B(x2,0)两点(点B在点A的右侧),其顶点P在线段MN上移动.M、N的坐标分别为(﹣1,2)、(1,2).x1的最小值为﹣3,则x2的最大值为( )
A.﹣1
B.1
C.3
D.5
解:抛物线顶点平移到点M时,由已知x1的最小值为﹣3
则设此时抛物线解析式为:y=a(x+1)2+2
把(﹣3,0)代入得
a=﹣
则当抛物线顶点平移到N时,解析式为y=﹣(x﹣1)2+2.
当y=0时,解得抛物线与x轴交点坐标为(3,0)或(﹣1,0)
则x2的最大值为3.
故选:C.
9.若抛物线y=x2﹣(m﹣3)x﹣m能与x轴交,则两交点间的距离最值是( )
A.最大值2
B.最小值2
C.最大值2
D.最小值2
解:设x1,x2是方程x2﹣(m﹣3)x﹣m=0的两根,抛物线y=x2﹣(m﹣3)x﹣m与x轴的交点为A、B,
∴x1+x2=m﹣3,x1?x2=﹣m.
∵两交点间的距离AB=|x1﹣x2|,
∴AB2=(x1﹣x2)2
=(x1+x2)2﹣4x1x2
=(m﹣3)2﹣4(﹣m)
=(m﹣1)2+8,
∴当m=1时,AB2有最小值8,
∴AB有最小值,即AB==2,
故选:D.
10.关于函数y=x2+2x﹣3的叙述:
①当x>1时,y的值随x的增大而增大;
②y的最小值是﹣3;
③函数图象与x轴交点的横坐标是方程x2+2x﹣3=0的根;
④函数图象与y轴交点的坐标是(0,﹣3);
⑤函数图象不经过第四象限.
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
解:①抛物线开口向上,对称轴为直线x=﹣1,故当x>1时,y的值随x的增大而增大,正确;
②y的最小值是=﹣4,错误;
③函数图象与x轴交点的横坐标是方程x2+2x﹣3=0的根,正确;
④令x=0,则y=﹣3,故函数图象与y轴交点的坐标是(0,﹣3),正确;
⑤函数图象经过四个象限,错误.
故选:B.
二.填空题(共5小题)
11.抛物线y=9x2﹣px+4与x轴只有一个公共点,则p的值是 ±12 .
解:根据题意:p2﹣4×9×4=0,
解得p=±12.
12.如图,在平面直角坐标系中,O为坐标原点,抛物线y=x2﹣2x与x轴正半轴交于点A,点B的坐标为(0,3).C是该抛物线第一象限图象上的一点,A,B,C三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点C的横坐标为m,若这个正方形的面积最小,则m的取值范围是 2<m≤3. .
解:∵抛物线y=x2﹣2x与x轴正半轴交于点A,
∴点A的坐标为(2,0),
如图所示:
当A,B,C三点均在某一个正方形的边上,
且该正方形的任何一条边均与某条坐标轴平行,
∵点B的坐标为(0,3),
正方形的面积最小时,
此时正方形的边长为3,
∴过点A、B、C的正方形的面积最小值为9,
∴S≥9.
当y=3时,
x2﹣2x=3,
解得x1=﹣1,x2=3,
∴当2<m≤3,时,
正方形面积有最小值;
当m=﹣1时,
正方形最小边长也为3,
正方形面积也有最小值,
∵C在第一象限,m>0,
综上所述:点C的横坐标m的取值范围是:
2<m≤3.
故答案为:2<m≤3.
13.如图,抛物线y1的顶点在y轴上,y2由y1平移得到,它们与x轴的交点为A、B、C,且2BC=3AB=4OD=6,若过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为 y=x .
解:解法一::∵2BC=3AB=4OD=6,
∴BC=3,AB=2,OD=,
则:A(﹣1,0)、B(1,0)、D(0,)、C(4,0),
把A(﹣1,0)、B(1,0)、D(0,)三点坐标代入:y=ax2+bx+c,
解得:y1=﹣x2+,顶点D(0,),
同理可得:y2=﹣x2+x﹣6=﹣(x﹣)2+,顶点E(,),
由平移可知:y1向右平移了个单位,再向上平移了个单位,得到y2,
所以过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线一定经过点(,),
设过原点的直线方程为:y=kx,(k>0),
则k=,
∴k=,
故:直线的解析式为y=x.
解法二:∵2BC=3AB=4OD=6,
∴BC=3,AB=2,OD=,
则:A(﹣1,0)、B(1,0)、D(0,)、C(4,0),
把A(﹣1,0)、B(1,0)、D(0,)三点坐标代入:y=ax2+bx+c,
解得:y1=﹣x2+…①,
同理可得:y2=﹣x2+x﹣6…②;
设:过原点的直线方程为:y=kx,(k>0)…③,
联立①、③得:3x2+2kx﹣3=0,
则:x1+x2=﹣,x1x2=﹣1,
则:G、F两点横坐标差=x2﹣x1===,
同理:K、H两点横坐标差=,
∵AG=KH,
∴=,
解得:k=,
故:直线的解析式为y=x.
14.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是 4 .
解:①∵(﹣1,0),(3,0)和(0,3)坐标都满足函数y=|x2﹣2x﹣3|,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线x=1,因此②也是正确的;
③根据函数的图象和性质,发现当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大,因此③也是正确的;
④函数图象的最低点就是与x轴的两个交点,根据y=0,求出相应的x的值为x=﹣1或x=3,因此④也是正确的;
⑤从图象上看,当x<﹣1或x>3,函数值要大于当x=1时的y=|x2﹣2x﹣3|=4,因此⑤是不正确的;
故答案是:4
15.如图,二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于点C,若AC⊥BC,则a的值为 .
解:∵∠ACB=90°,CO⊥AB,根据射影定理可得CO2=AO×BO.
根据抛物线的解析式可知OC=2,设A(m,0),B(n,0),则m和n是方程ax2+bx+2=0的两个根,
所以mn=.
∴22=﹣mn=﹣,解得a=﹣.
故答案为﹣
三.解答题(共5小题)
16.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5,
(2)当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD=×AC×PD=2(﹣x2+5x)=﹣2x2+10x=﹣2(x﹣)2+,
∵﹣2<0
∴当x=时,
∴即:点P(,)时,S四边形APCD最大=.
17.已知k是常数,抛物线y=x2+(k2+k﹣6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在物线y=x2+(k2+k﹣6)x+3k上,且P到y轴的距离是2,求点P的坐标.
解:(1)∵抛物线y=x2+(k2+k﹣6)x+3k的对称轴是y轴,
∴k2+k﹣6=0,解得k1=﹣3,k2=2;
又∵抛物线y=x2+(k2+k﹣6)x+3k与x轴有两个交点.
∴3k<0
∴k=﹣3.此时抛物线的关系式为y=x2﹣9,
因此k的值为﹣3.
(2)∵点P在抛物线y=x2﹣9上,且P到y轴的距离是2,
∴点P的横坐标为2或﹣2,
当x=2时,y=﹣5
当x=﹣2时,y=﹣5.
∴P(2,﹣5)或P(﹣2,﹣5)
因此点P的坐标为:P(2,﹣5)或P(﹣2,﹣5).
18.在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx﹣,经过点A(﹣1,0)、B(5,0).
(1)求此抛物线顶点C的坐标;
(2)联结AC交y轴于点D,联结BD、BC,过点C作CH⊥BD,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
解:(1)把A(﹣1,0)、B(5,0)代入抛物线解析式,
得:,解得:,
∴抛物线的解析式为:,
∴顶点C(2,﹣3)
(2)方法一:设BD与CG相交于点P,
设直线AC的解析式为:y=kx+b
把A(﹣1,0)和C(2,﹣3)代入得:
解得:
则直线AC:y=﹣x﹣1,
∴D(0,﹣1),
同理可得直线BD:y=x﹣1,
∴
∵∠CHP=∠PGB=90°,∠GPB=∠CPH
∴△BPG∽△CPH,
∴
∴△HPG∽△CPB,
∴,
∴,
∴;
方法二:如图2,过点H作HM⊥CG于M,
∵,,,
∴BD2=CD2+BC2,
∴∠BCD=90°,
∵S△BCD=BD?CH=BC?CD,
∴,
∵∠ABD=∠HCG,
∴△OBD∽△MCH,
∴,
∴,,
∴,
由勾股定理得:GH=
∴,
方法三:直线AC:y=﹣x﹣1,
∴D(0,﹣1),
直线BD:y=x﹣1,
∵CH⊥BD,
∴kBD?kCH=﹣1,
∴直线CH:y=﹣5x+7,
联立解析式:,解得:,
∴H(,﹣),
∴.
19.求出y=2(x﹣1)2﹣8与坐标轴的交点坐标,直接写出y>0时x的取值范围.
解:y=2(x﹣1)2﹣8,
令x=0,则y=﹣6;
令y=0,则0=2(x﹣1)2﹣8,
解得x=3,或x=﹣1,
∴抛物线与y轴交于(0,﹣6),与x轴交于(3,0)或(﹣1,0),
当y>0时,x的取值范围为x>3或x<﹣1.
20.利用二次函数的图象,求下列一元二次方程的近似根.
(1)x2+11x=9;
(2)x2+3x+2=0;
(3)x2+2x﹣9=0;
(4)x2+3=3x.
解:(1)如图1:
方程的近似根为x1≈0.8,x2≈﹣11.8;
(2)如图2:
方程的根为x1=﹣1.0,x2=﹣2.0;
(3)如图3:
方程的近似根为x1≈﹣4.2,x2≈2.2;
(4)如图4:
方程没有实数解.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
