23.1 图形的旋转 高频易错题集 (原卷+解析)
文档属性
| 名称 | 23.1 图形的旋转 高频易错题集 (原卷+解析) |  | |
| 格式 | zip | ||
| 文件大小 | 690.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 09:52:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
23.1
图形的旋转
高频易错题集
一.选择题(共10小题)
1.摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,3号车厢才会运行到最高点?( )
A.14分钟
B.20分钟
C.15
分钟
D.分钟
2.一辆模型赛车,先前进1m,然后沿原地逆时针方向旋转,旋转角为α(0<α<90°),被称为一次操作,若五次操作后,发现赛车回到出发点,则旋转角α为( )
A.108°
B.120°
C.72°
D.36°
3.下列事件中,属于旋转运动的是( )
A.小明向北走了4米
B.时针转动
C.电梯从1楼到12楼
D.一物体从高空坠下
4.如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )
A.15
B.18
C.20
D.24
5.如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A.
B.
C.4
D.6
6.如图,直线c与直线a相交于点A,与直线b相交于点B,∠1=130°,∠2=60°,若要使直线a∥b,则将直线a绕点A按如图所示的方向至少旋转( )
A.10°
B.20°
C.60°
D.130°
7.下列图形中,绕某个点旋转72度后能与自身重合的是( )
A.
B.
C.
D.
8.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
9.如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A.216°
B.144°
C.108°
D.72°
10.如图,已知点O(0,0),P(1,2),将线段PO绕点P按顺时针方向以每秒90°的速度旋转,则第19秒时,点O的对应点坐标为( )
A.(0,0)
B.(3,1)
C.(﹣1,3)
D.(2,4)
二.填空题(共5小题)
11.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是
.
12.图中,甲图怎样变成乙图:
.
13.如图,将△ABC绕点C顺时针方向旋转40°得到△A′CB′,若AC⊥A′B′,则∠BAC=
°.
14.如图,△ABC中,∠ACB=90°,∠A=25°,将△ABC绕点C逆时针旋转至△DEC的位置,点B恰好在边DE上,则∠θ=
度.
15.如图,可以看作是由其中一个菱形至少经过
次旋转得到的,旋转角的度数是
.
三.解答题(共5小题)
16.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
17.如图,钟摆的摆动是旋转,图中的旋转中心是哪一点?试用量角器测量旋转角度的大小.(精确到1°)
18.已知,在等边△ABC中,点E在BA的延长线上,点D在BC上,且ED=EC
(1)如图1,求证:AE=DB;
(2)如图2,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于AB的长.
19.阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=
;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
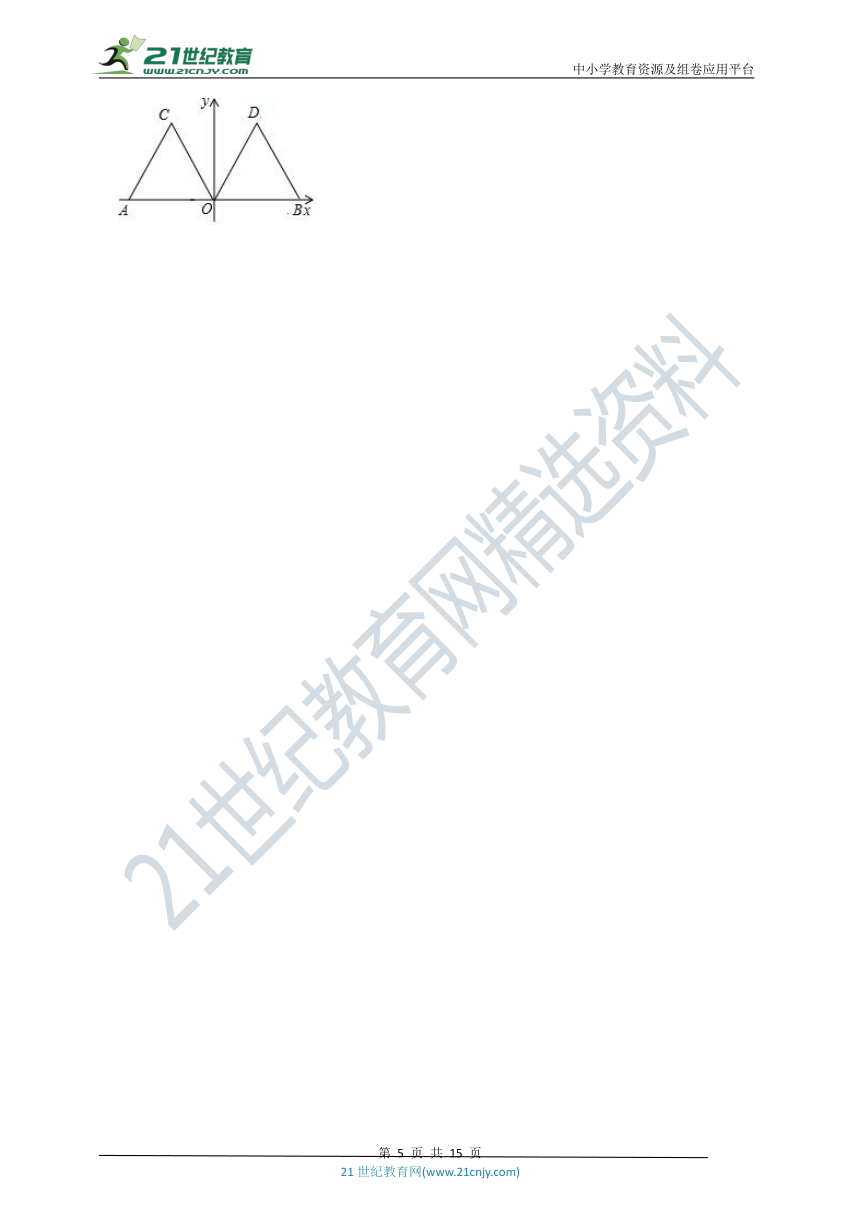
20.如图,点O为平面直角坐标系的原点,点A在x轴上,△AOC是边长为2的等边三角形.
(1)写出△AOC的顶点C的坐标:
.
(2)将△AOC沿x轴向右平移得到△OBD,则平移的距离是
(3)将△AOC绕原点O顺时针旋转得到△DOB,则旋转角可以是
度
(4)连接AD,交OC于点E,求∠AEO的度数.
试题解析
一.选择题(共10小题)
1.摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,3号车厢才会运行到最高点?( )
解:(分钟).
所以经过15分钟后,3号车厢才会运行到最高点.
故选:C.
2.一辆模型赛车,先前进1m,然后沿原地逆时针方向旋转,旋转角为α(0<α<90°),被称为一次操作,若五次操作后,发现赛车回到出发点,则旋转角α为( )
A.108°
B.120°
C.72°
D.36°
解:由题意,得赛车所走路线为正五边形,正五边形外角之和为360°,
所以五次旋转角之和为360°,
所以α=360°÷5=72°.
故选:C.
3.下列事件中,属于旋转运动的是( )
A.小明向北走了4米
B.时针转动
C.电梯从1楼到12楼
D.一物体从高空坠下
解:A.小明向北走了4米是平移,不合题意;
B.时针转动是旋转运动,符合题意;
C.电梯从1楼到12楼是平移,不合题意;
D.一物体从高空坠下是平移,不合题意;
故选:B.
4.如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )
A.15
B.18
C.20
D.24
解:设HD=x,由已知HC=x+8
∵P是CH的中点
∴HP=
有图形可知,△HPA中,边HP和边AP边上高相等
∴由面积法HP=AP
∴AP=4+
∵DP=HP﹣HD=4﹣
∴Rt△APD中
AP2=DP2+AD2
∴(4+)2=(4﹣)2+62
解得x=
∴HP=4+=
∴Rt△ADH中,
HA=
∴△APH的周长为=20
故选:C.
5.如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A.
B.
C.4
D.6
解:∵将△ABC绕点A逆时针旋转60°得到△AB1C1,
∴AC=AC1=2,∠CAC1=60°,
∵AB=3,AC=2,∠BAC=30°,
∴∠BAC1=90°,
∴在Rt△BAC1中,BC1==.
故选:B.
6.如图,直线c与直线a相交于点A,与直线b相交于点B,∠1=130°,∠2=60°,若要使直线a∥b,则将直线a绕点A按如图所示的方向至少旋转( )
A.10°
B.20°
C.60°
D.130°
解:∵∠2=60°,
∴若要使直线a∥b,则∠3应该为60°,
又∵∠1=130°,
∴∠3=50°,
∴直线a绕点A按顺时针方向至少旋转:60°﹣50°=10°,
故选:A.
7.下列图形中,绕某个点旋转72度后能与自身重合的是( )
A.
B.
C.
D.
解:A.旋转90°后能与自身重合,不合题意;
B.旋转72°后能与自身重合,符合题意;
C.旋转60°后能与自身重合,不合题意;
D.旋转45°后能与自身重合,不合题意;
故选:B.
8.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
9.如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A.216°
B.144°
C.108°
D.72°
解:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,
因而A、B、D选项都正确,不能与其自身重合的是C选项.
故选:C.
10.如图,已知点O(0,0),P(1,2),将线段PO绕点P按顺时针方向以每秒90°的速度旋转,则第19秒时,点O的对应点坐标为( )
A.(0,0)
B.(3,1)
C.(﹣1,3)
D.(2,4)
解:如图所示,∵线段PO绕点P按顺时针方向以每秒90°的速度旋转,每4秒一个循环,19=4×4+3,
∴3×90°=270°,
∴19秒后点O旋转到点O'的位置,∠OPO'=90°,
如图所示,过P作MN⊥y轴于点M,过O'作O'N⊥MN于点N,
则∠OMP=∠PNO'=90°,∠POM=∠O'PN,OP=PO',
∴△OPM≌△PO'N(AAS),
∴O'N=PM=1,PN=OM=2,
∴MN=1+2=3,点O'离x轴的距离为2﹣1=1,
∴点O'的坐标为(3,1),
故选:B.
二.填空题(共5小题)
11.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是 6秒或19.5秒 .
解:设A灯旋转时间为t秒,B灯光束第一次到达BQ需要180÷4=45(秒),
∴t≤45﹣12,即t≤33.
由题意,满足以下条件时,两灯的光束能互相平行:
①如图1,∠MAM'=∠PBP',12t=4(12+t),解得t=6;
②如图2,∠NAM'+∠PBP'=180°,12t﹣180+4(12+t)=180,解得t=19.5;
综上所述,满足条件的t的值为6秒或19.5秒.
故答案为:6秒或19.5秒.
12.图中,甲图怎样变成乙图: 绕点A顺时针旋转 .
解:观察可知,甲图绕点A顺时针旋转即可变成乙图.
故答案为:绕点A顺时针旋转.
13.如图,将△ABC绕点C顺时针方向旋转40°得到△A′CB′,若AC⊥A′B′,则∠BAC= 50 °.
解:∵△ABC绕点C顺时针方向旋转40°得到△A′CB′,
∴∠ACA'=40°,
∵AC⊥A′B′,
∴Rt△A'CD中,∠DA'C=90°﹣∠DCA'=90°﹣40°=50°,
由旋转可得,∠BAC=∠A'=50°.
故答案为:50.
14.如图,△ABC中,∠ACB=90°,∠A=25°,将△ABC绕点C逆时针旋转至△DEC的位置,点B恰好在边DE上,则∠θ= 50 度.
解:∵∠ACB=90°,∠A=25°,
∴∠ABC=65°,
由旋转的性质可知,∠E=∠ABC=65°,CE=CB,∠ECB=∠DCA,
∴∠ECB=50°,
∴∠θ=50°,
故答案为:50.
15.如图,可以看作是由其中一个菱形至少经过 5 次旋转得到的,旋转角的度数是 60° .
解:由图可得,可以看作是由其中一个菱形至少经过5次旋转得到的,旋转角的度数是60°.
故答案为:5,60°.
三.解答题(共5小题)
16.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
解:我能,方法如下:
图(1)与图(2)中扑克牌完全一样,说明被旋转过的牌是中心对称图形,
而图中只有方块4是中心对称图形,故方块4被旋转过.
17.如图,钟摆的摆动是旋转,图中的旋转中心是哪一点?试用量角器测量旋转角度的大小.(精确到1°)
解:图中的旋转中心是点O,
旋转角度的大小约为30°.
18.已知,在等边△ABC中,点E在BA的延长线上,点D在BC上,且ED=EC
(1)如图1,求证:AE=DB;
(2)如图2,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于AB的长.
解:(1)如图,作DK∥AC交AB于K,则△BDK是等边三角形,
∵△ABC是等边三角形,
∴∠EKD=∠EAC=120°,∠B=∠BKD=60°,
∴DK=BD,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠B+∠KED=∠EDC,
∵∠ECA+∠ACB=∠ECD,
∴∠B+∠KED=∠ECA+∠ACB,
∵∠B=∠ACB=60°,
∴∠KED=∠ECA,
在△DKE与△EAC中,
,
∴△DKE≌△EAC(AAS),
∴AE=DK,
∴BD=AE.
(2)BE﹣AE=AB;BE﹣BD=AB;AF﹣AE=AB;AF﹣BD=AB.
理由:由旋转可得,△BCE≌△ACF,
∴BE=AF,
又∵BD=AE,AB=BE﹣AE,
∴BE﹣AE=AB;BE﹣BD=AB;AF﹣AE=AB;AF﹣BD=AB.
19.阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB= 150° ;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
解:(1)∵△ACP′≌△ABP,
∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,
由题意知旋转角∠PA
P′=60°,
∴△AP
P′为等边三角形,
P
P′=AP=3,∠A
P′P=60°,
易证△P
P′C为直角三角形,且∠P
P′C=90°,
∴∠APB=∠AP′C=∠A
P′P+∠P
P′C=60°+90°=150°;
故答案为:150°;
(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠CAE′+∠CAF=∠BAE+∠CAF=∠BAC﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,
即EF2=BE2+FC2.
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,
∴AB=2,
∴BC=,
∵△AOB绕点B顺时针方向旋转60°,
∴△A′O′B如图所示;
∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C=,
∴OA+OB+OC=A′O′+OO′+OC=A′C=.
20.如图,点O为平面直角坐标系的原点,点A在x轴上,△AOC是边长为2的等边三角形.
(1)写出△AOC的顶点C的坐标: (﹣1,) .
(2)将△AOC沿x轴向右平移得到△OBD,则平移的距离是 2
(3)将△AOC绕原点O顺时针旋转得到△DOB,则旋转角可以是 120 度
(4)连接AD,交OC于点E,求∠AEO的度数.
解:(1)如图,过C作CH⊥AO于H,则HO=AO=1,
∴Rt△COH中,CH==,
∴点C的坐标为(﹣1,),
故答案为:(﹣1,);
(2)由平移可得,平移的距离=AO=2,
故答案为:2;
(3)由旋转可得,旋转角=∠AOD=120°,
故答案为:120;
(4)如图,∵AC∥OD,
∴∠CAE=∠ODE,∠ACE=∠DOE,
又∵AC=DO,
∴△ACE≌△DOE,
∴CE=OE,
∴AD⊥CO,即∠AEO=90°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
23.1
图形的旋转
高频易错题集
一.选择题(共10小题)
1.摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,3号车厢才会运行到最高点?( )
A.14分钟
B.20分钟
C.15
分钟
D.分钟
2.一辆模型赛车,先前进1m,然后沿原地逆时针方向旋转,旋转角为α(0<α<90°),被称为一次操作,若五次操作后,发现赛车回到出发点,则旋转角α为( )
A.108°
B.120°
C.72°
D.36°
3.下列事件中,属于旋转运动的是( )
A.小明向北走了4米
B.时针转动
C.电梯从1楼到12楼
D.一物体从高空坠下
4.如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )
A.15
B.18
C.20
D.24
5.如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A.
B.
C.4
D.6
6.如图,直线c与直线a相交于点A,与直线b相交于点B,∠1=130°,∠2=60°,若要使直线a∥b,则将直线a绕点A按如图所示的方向至少旋转( )
A.10°
B.20°
C.60°
D.130°
7.下列图形中,绕某个点旋转72度后能与自身重合的是( )
A.
B.
C.
D.
8.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
9.如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A.216°
B.144°
C.108°
D.72°
10.如图,已知点O(0,0),P(1,2),将线段PO绕点P按顺时针方向以每秒90°的速度旋转,则第19秒时,点O的对应点坐标为( )
A.(0,0)
B.(3,1)
C.(﹣1,3)
D.(2,4)
二.填空题(共5小题)
11.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是
.
12.图中,甲图怎样变成乙图:
.
13.如图,将△ABC绕点C顺时针方向旋转40°得到△A′CB′,若AC⊥A′B′,则∠BAC=
°.
14.如图,△ABC中,∠ACB=90°,∠A=25°,将△ABC绕点C逆时针旋转至△DEC的位置,点B恰好在边DE上,则∠θ=
度.
15.如图,可以看作是由其中一个菱形至少经过
次旋转得到的,旋转角的度数是
.
三.解答题(共5小题)
16.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
17.如图,钟摆的摆动是旋转,图中的旋转中心是哪一点?试用量角器测量旋转角度的大小.(精确到1°)
18.已知,在等边△ABC中,点E在BA的延长线上,点D在BC上,且ED=EC
(1)如图1,求证:AE=DB;
(2)如图2,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于AB的长.
19.阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=
;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
20.如图,点O为平面直角坐标系的原点,点A在x轴上,△AOC是边长为2的等边三角形.
(1)写出△AOC的顶点C的坐标:
.
(2)将△AOC沿x轴向右平移得到△OBD,则平移的距离是
(3)将△AOC绕原点O顺时针旋转得到△DOB,则旋转角可以是
度
(4)连接AD,交OC于点E,求∠AEO的度数.
试题解析
一.选择题(共10小题)
1.摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,3号车厢才会运行到最高点?( )
解:(分钟).
所以经过15分钟后,3号车厢才会运行到最高点.
故选:C.
2.一辆模型赛车,先前进1m,然后沿原地逆时针方向旋转,旋转角为α(0<α<90°),被称为一次操作,若五次操作后,发现赛车回到出发点,则旋转角α为( )
A.108°
B.120°
C.72°
D.36°
解:由题意,得赛车所走路线为正五边形,正五边形外角之和为360°,
所以五次旋转角之和为360°,
所以α=360°÷5=72°.
故选:C.
3.下列事件中,属于旋转运动的是( )
A.小明向北走了4米
B.时针转动
C.电梯从1楼到12楼
D.一物体从高空坠下
解:A.小明向北走了4米是平移,不合题意;
B.时针转动是旋转运动,符合题意;
C.电梯从1楼到12楼是平移,不合题意;
D.一物体从高空坠下是平移,不合题意;
故选:B.
4.如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )
A.15
B.18
C.20
D.24
解:设HD=x,由已知HC=x+8
∵P是CH的中点
∴HP=
有图形可知,△HPA中,边HP和边AP边上高相等
∴由面积法HP=AP
∴AP=4+
∵DP=HP﹣HD=4﹣
∴Rt△APD中
AP2=DP2+AD2
∴(4+)2=(4﹣)2+62
解得x=
∴HP=4+=
∴Rt△ADH中,
HA=
∴△APH的周长为=20
故选:C.
5.如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A.
B.
C.4
D.6
解:∵将△ABC绕点A逆时针旋转60°得到△AB1C1,
∴AC=AC1=2,∠CAC1=60°,
∵AB=3,AC=2,∠BAC=30°,
∴∠BAC1=90°,
∴在Rt△BAC1中,BC1==.
故选:B.
6.如图,直线c与直线a相交于点A,与直线b相交于点B,∠1=130°,∠2=60°,若要使直线a∥b,则将直线a绕点A按如图所示的方向至少旋转( )
A.10°
B.20°
C.60°
D.130°
解:∵∠2=60°,
∴若要使直线a∥b,则∠3应该为60°,
又∵∠1=130°,
∴∠3=50°,
∴直线a绕点A按顺时针方向至少旋转:60°﹣50°=10°,
故选:A.
7.下列图形中,绕某个点旋转72度后能与自身重合的是( )
A.
B.
C.
D.
解:A.旋转90°后能与自身重合,不合题意;
B.旋转72°后能与自身重合,符合题意;
C.旋转60°后能与自身重合,不合题意;
D.旋转45°后能与自身重合,不合题意;
故选:B.
8.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
9.如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A.216°
B.144°
C.108°
D.72°
解:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,
因而A、B、D选项都正确,不能与其自身重合的是C选项.
故选:C.
10.如图,已知点O(0,0),P(1,2),将线段PO绕点P按顺时针方向以每秒90°的速度旋转,则第19秒时,点O的对应点坐标为( )
A.(0,0)
B.(3,1)
C.(﹣1,3)
D.(2,4)
解:如图所示,∵线段PO绕点P按顺时针方向以每秒90°的速度旋转,每4秒一个循环,19=4×4+3,
∴3×90°=270°,
∴19秒后点O旋转到点O'的位置,∠OPO'=90°,
如图所示,过P作MN⊥y轴于点M,过O'作O'N⊥MN于点N,
则∠OMP=∠PNO'=90°,∠POM=∠O'PN,OP=PO',
∴△OPM≌△PO'N(AAS),
∴O'N=PM=1,PN=OM=2,
∴MN=1+2=3,点O'离x轴的距离为2﹣1=1,
∴点O'的坐标为(3,1),
故选:B.
二.填空题(共5小题)
11.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是 6秒或19.5秒 .
解:设A灯旋转时间为t秒,B灯光束第一次到达BQ需要180÷4=45(秒),
∴t≤45﹣12,即t≤33.
由题意,满足以下条件时,两灯的光束能互相平行:
①如图1,∠MAM'=∠PBP',12t=4(12+t),解得t=6;
②如图2,∠NAM'+∠PBP'=180°,12t﹣180+4(12+t)=180,解得t=19.5;
综上所述,满足条件的t的值为6秒或19.5秒.
故答案为:6秒或19.5秒.
12.图中,甲图怎样变成乙图: 绕点A顺时针旋转 .
解:观察可知,甲图绕点A顺时针旋转即可变成乙图.
故答案为:绕点A顺时针旋转.
13.如图,将△ABC绕点C顺时针方向旋转40°得到△A′CB′,若AC⊥A′B′,则∠BAC= 50 °.
解:∵△ABC绕点C顺时针方向旋转40°得到△A′CB′,
∴∠ACA'=40°,
∵AC⊥A′B′,
∴Rt△A'CD中,∠DA'C=90°﹣∠DCA'=90°﹣40°=50°,
由旋转可得,∠BAC=∠A'=50°.
故答案为:50.
14.如图,△ABC中,∠ACB=90°,∠A=25°,将△ABC绕点C逆时针旋转至△DEC的位置,点B恰好在边DE上,则∠θ= 50 度.
解:∵∠ACB=90°,∠A=25°,
∴∠ABC=65°,
由旋转的性质可知,∠E=∠ABC=65°,CE=CB,∠ECB=∠DCA,
∴∠ECB=50°,
∴∠θ=50°,
故答案为:50.
15.如图,可以看作是由其中一个菱形至少经过 5 次旋转得到的,旋转角的度数是 60° .
解:由图可得,可以看作是由其中一个菱形至少经过5次旋转得到的,旋转角的度数是60°.
故答案为:5,60°.
三.解答题(共5小题)
16.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
解:我能,方法如下:
图(1)与图(2)中扑克牌完全一样,说明被旋转过的牌是中心对称图形,
而图中只有方块4是中心对称图形,故方块4被旋转过.
17.如图,钟摆的摆动是旋转,图中的旋转中心是哪一点?试用量角器测量旋转角度的大小.(精确到1°)
解:图中的旋转中心是点O,
旋转角度的大小约为30°.
18.已知,在等边△ABC中,点E在BA的延长线上,点D在BC上,且ED=EC
(1)如图1,求证:AE=DB;
(2)如图2,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于AB的长.
解:(1)如图,作DK∥AC交AB于K,则△BDK是等边三角形,
∵△ABC是等边三角形,
∴∠EKD=∠EAC=120°,∠B=∠BKD=60°,
∴DK=BD,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠B+∠KED=∠EDC,
∵∠ECA+∠ACB=∠ECD,
∴∠B+∠KED=∠ECA+∠ACB,
∵∠B=∠ACB=60°,
∴∠KED=∠ECA,
在△DKE与△EAC中,
,
∴△DKE≌△EAC(AAS),
∴AE=DK,
∴BD=AE.
(2)BE﹣AE=AB;BE﹣BD=AB;AF﹣AE=AB;AF﹣BD=AB.
理由:由旋转可得,△BCE≌△ACF,
∴BE=AF,
又∵BD=AE,AB=BE﹣AE,
∴BE﹣AE=AB;BE﹣BD=AB;AF﹣AE=AB;AF﹣BD=AB.
19.阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB= 150° ;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
解:(1)∵△ACP′≌△ABP,
∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,
由题意知旋转角∠PA
P′=60°,
∴△AP
P′为等边三角形,
P
P′=AP=3,∠A
P′P=60°,
易证△P
P′C为直角三角形,且∠P
P′C=90°,
∴∠APB=∠AP′C=∠A
P′P+∠P
P′C=60°+90°=150°;
故答案为:150°;
(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠CAE′+∠CAF=∠BAE+∠CAF=∠BAC﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,
即EF2=BE2+FC2.
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,
∴AB=2,
∴BC=,
∵△AOB绕点B顺时针方向旋转60°,
∴△A′O′B如图所示;
∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C=,
∴OA+OB+OC=A′O′+OO′+OC=A′C=.
20.如图,点O为平面直角坐标系的原点,点A在x轴上,△AOC是边长为2的等边三角形.
(1)写出△AOC的顶点C的坐标: (﹣1,) .
(2)将△AOC沿x轴向右平移得到△OBD,则平移的距离是 2
(3)将△AOC绕原点O顺时针旋转得到△DOB,则旋转角可以是 120 度
(4)连接AD,交OC于点E,求∠AEO的度数.
解:(1)如图,过C作CH⊥AO于H,则HO=AO=1,
∴Rt△COH中,CH==,
∴点C的坐标为(﹣1,),
故答案为:(﹣1,);
(2)由平移可得,平移的距离=AO=2,
故答案为:2;
(3)由旋转可得,旋转角=∠AOD=120°,
故答案为:120;
(4)如图,∵AC∥OD,
∴∠CAE=∠ODE,∠ACE=∠DOE,
又∵AC=DO,
∴△ACE≌△DOE,
∴CE=OE,
∴AD⊥CO,即∠AEO=90°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
