24.1.2 垂直于弦的直径 高频易错题集 (原卷+解析)
文档属性
| 名称 | 24.1.2 垂直于弦的直径 高频易错题集 (原卷+解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 618.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.1.2
垂直于弦的直径
高频易错题集
一.选择题(共10小题)
1.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17
B.18
C.19
D.20
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的直径为( )
A.10
B.8
C.5
D.3
3.如图,直线y=﹣x+4与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为( )
A.
B.
C.
D.
4.过⊙O内一点M的最长弦为20cm,最短弦为16cm,那么OM的长为( )
A.3cm
B.6cm
C.8cm
D.9cm
5.如图,⊙O经过菱形ABCO的顶点A、B、C,若OP⊥AB交⊙O于点P,则∠PAB的大小为( )
A.15°
B.20°
C.25°
D.30°
6.如图,在⊙O中,C为弦AB上一点,AC=2,BC=6,⊙O的半径为5,则OC=( )
A.
B.4
C.3
D.
7.如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
8.下列命题中,不正确的是( )
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弧
9.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有( )
A.1组
B.2组
C.3组
D.4组
10.下列命题中,正确的是( )
A.垂直于弦的直径平分弦,并且平分弦所对的弧
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.AB,CD是⊙O的弦,若AB=CD,则AB∥CD
D.圆是轴对称图形,对称轴是圆的每一条直径
二.填空题(共5小题)
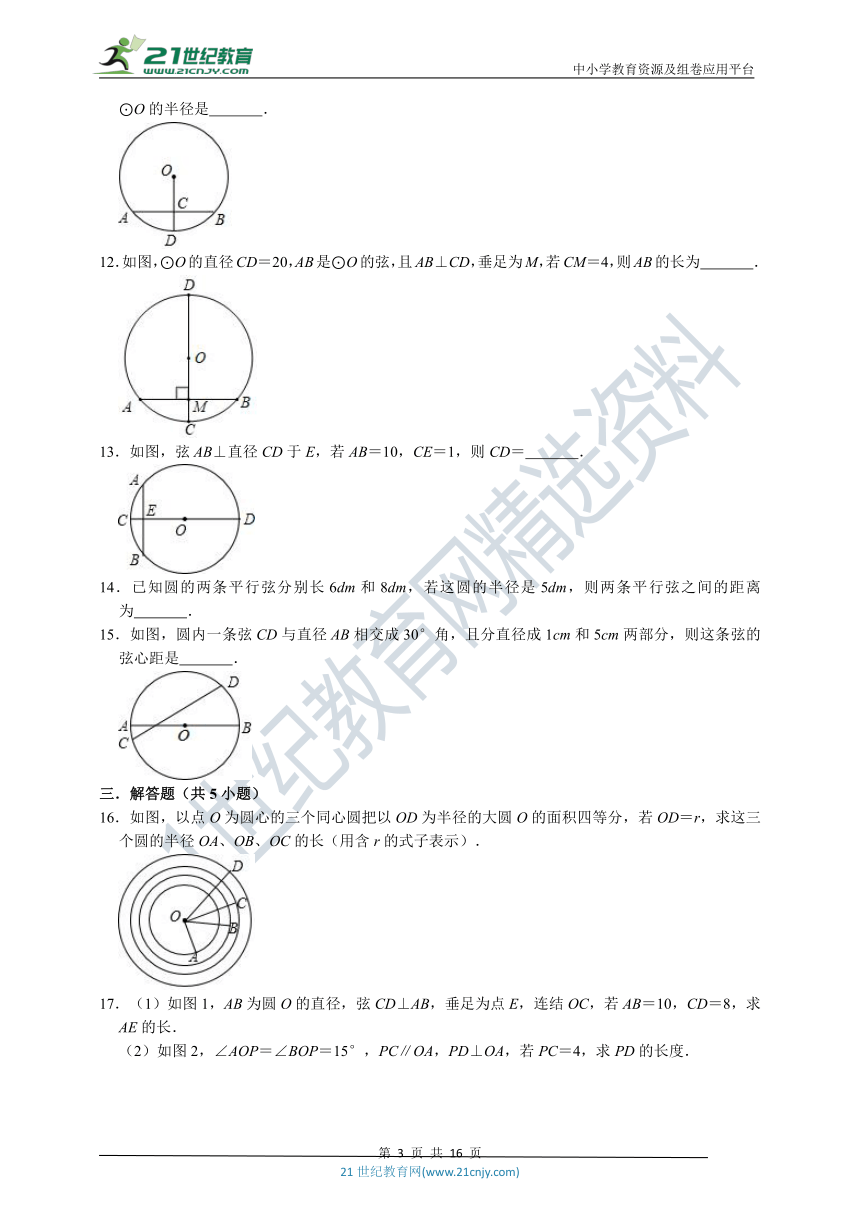
11.如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是
.
12.如图,⊙O的直径CD=20,AB是⊙O的弦,且AB⊥CD,垂足为M,若CM=4,则AB的长为
.
13.如图,弦AB⊥直径CD于E,若AB=10,CE=1,则CD=
.
14.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为
.
15.如图,圆内一条弦CD与直径AB相交成30°角,且分直径成1cm和5cm两部分,则这条弦的弦心距是
.
三.解答题(共5小题)
16.如图,以点O为圆心的三个同心圆把以OD为半径的大圆O的面积四等分,若OD=r,求这三个圆的半径OA、OB、OC的长(用含r的式子表示).
17.(1)如图1,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若AB=10,CD=8,求AE的长.
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.
18.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长.
19.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
20.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
试题解析
一.选择题(共10小题)
1.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17
B.18
C.19
D.20
解:连接OP,OQ,分别交AC,BC于H,I,
∵M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q,
∴OP⊥AC,OQ⊥BC,由对称性可知:H,P,M三点共线,I,Q,N三点共线,
∴H、I是AC、BC的中点,
∴OH+OI=(AC+BC)=13,
∵MH+NI=AC+BC=13,MP+NQ=7,
∴PH+QI=13﹣7=6,
∴AB=OP+OQ=OH+OI+PH+QI=13+6=19,
故选:C.
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的直径为( )
A.10
B.8
C.5
D.3
解:连接OC,
∵CD⊥AB,CD=8,
∴PC=CD=×8=4,
在Rt△OCP中,设OC=x,则OA=x,
∵PC=4,OP=AP﹣OA=8﹣x,
∴OC2=PC2+OP2,
即x2=42+(8﹣x)2,
解得x=5,
∴⊙O的直径为10.
故选:A.
3.如图,直线y=﹣x+4与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为( )
A.
B.
C.
D.
解:连接AO,并延长交直线CD于G,连接AQ,
∵Q是MN的中点.
∴AQ⊥MN,
∵A的坐标为(﹣4,﹣4),
∴直线AO:y=x,AO=4,
∵直线CD:y=﹣x+4,
∴AO⊥CD,
∴∠AQO=∠OGP=90°,
∵∠AOQ=∠POG,
∴∠AOQ∽△POG,
∴,
当x=0时,y=4,当y=0时,x=4,
∴OC=OD=4,
∴OG=CD=2,
∵OP=t,OQ=S,
∴,
S=,
故选项C、D不正确;
当OP=2时,即S=OQ=4,t=2,直线OP过圆心A,此时Q与A重合,此种情况成立,
故选项B不正确;
故选:A.
4.过⊙O内一点M的最长弦为20cm,最短弦为16cm,那么OM的长为( )
A.3cm
B.6cm
C.8cm
D.9cm
解:由题意知,最长的弦为直径,最短的弦为垂直于直径的弦,
如图所示.直径ED⊥AB于点M,
则ED=20cm,AB=16cm,
由垂径定理知:点M为AB中点,
∴AM=8cm,
∵半径OA=10cm,
∴OM2=OA2﹣AM2=100﹣64=6,
∴OM=6cm.
故选:B.
5.如图,⊙O经过菱形ABCO的顶点A、B、C,若OP⊥AB交⊙O于点P,则∠PAB的大小为( )
A.15°
B.20°
C.25°
D.30°
解:连接OB,
∵四边形ABCO是菱形,
∴OA=AB,
∵OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∵OP⊥AB,
∴∠BOP=∠AOB=30°,
由圆周角定理得,∠PAB=∠BOP=15°,
故选:A.
6.如图,在⊙O中,C为弦AB上一点,AC=2,BC=6,⊙O的半径为5,则OC=( )
A.
B.4
C.3
D.
解:设OC=x,利用圆内相交弦定理可得:2×6=(5﹣x)(5+x)
解得x=.
故选:A.
7.如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
解:作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
由垂径定理、勾股定理得:OM=ON==3,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=3
故选:C.
8.下列命题中,不正确的是( )
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弧
解:A、根据垂径定理的推论可知,垂直平分弦的直线经过圆心;故本答案正确.
B、直径是最长的弦,任意两条直径互相平分,但不一定互相垂直,故被平分的弦不能是直径;故本答案错误.
C、如图所示,两弦平行,则圆周角相等,圆周角相等,则弧相等;故本选项正确.
D、根据垂径定理可知,垂直于弦的直径必平分弦所对的弧;故本选项正确.
故选:B.
9.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有( )
A.1组
B.2组
C.3组
D.4组
解:由垂径定理知,点H是AB的中点,也是CD的中点,则有CH=HD,AH=HB,所以AD=BC,AC=BD.
所以共有4组相等的线段.
故选:D.
10.下列命题中,正确的是( )
A.垂直于弦的直径平分弦,并且平分弦所对的弧
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.AB,CD是⊙O的弦,若AB=CD,则AB∥CD
D.圆是轴对称图形,对称轴是圆的每一条直径
解:A、垂直于弦的直径平分弦,且平分弦所对的弧,故本选项正确;
B、平分弦(弦不是直径)直径垂直于弦,并且平分弦所对的弧,故本选项错误;
C、AB和CD可能相交,故本选项错误;
D、圆是轴对称图形,对称轴是圆的每一条直径所在的直线,故本选项错误;
故选:A.
二.填空题(共5小题)
11.如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是 .
解:连接OA,
∵C是AB的中点,
∴AC=AB=2,OC⊥AB,
∴OA2=OC2+AC2,即OA2=(OA﹣1)2+22,
解得,OA=,
故答案为:.
12.如图,⊙O的直径CD=20,AB是⊙O的弦,且AB⊥CD,垂足为M,若CM=4,则AB的长为 16 .
解:连接OA,
∵⊙O的直径CD=20,
∴OA=OC=10,
∵CM=4,
∴OM=10﹣4=6,
在Rt△OAM中,由勾股定理得:AM==8,
∴由垂径定理得:AB=2AM=16.
故答案为:16.
13.如图,弦AB⊥直径CD于E,若AB=10,CE=1,则CD= 26 .
解:连接OA,
∵弦AB⊥直径CD于E,
∴AE=EB=5,
设圆的半径为r,则OE=r﹣1,
由勾股定理得,r2=52+(r﹣1)2,
解得,r=13,
则CD=2r=26,
故答案为:26.
14.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为 7dm或1dm .
解:如图,AB∥CD,AB=6dm,CD=8dm,
过O点作OE⊥AB于E,交CD于F点,连OA、OC,
∴AE=BE=AB=3,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴CF=FD=CD=4,
在Rt△OAE中,OA=5dm
OE===4,
同理可得OF=3,
当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7(dm);
当圆心O不在AB与CD之间时,AB与CD的距离=OE﹣OF=4﹣3=1(dm).
故答案为7dm或1dm.
15.如图,圆内一条弦CD与直径AB相交成30°角,且分直径成1cm和5cm两部分,则这条弦的弦心距是 1cm .
解:过点O作OF⊥CD于点F,设弦CD与直径AB相交于点E,
∵分直径成1cm和5cm两部分,
∴AB=6cm,
∴OA=AB=3cm,
∴OE=OA﹣AE=2cm,
∵∠OEF=30°,
∴OF=OE=1(cm).
故答案为:1cm.
三.解答题(共5小题)
16.如图,以点O为圆心的三个同心圆把以OD为半径的大圆O的面积四等分,若OD=r,求这三个圆的半径OA、OB、OC的长(用含r的式子表示).
解:∵π?OA2=π?r2,
∴OA2=r2,
∴OA=r;
∵π?OB2=π?r2,
∴OB2=r2,
∴OB=r;
∵π?OC2=π?r2,
∴OC2=r2,
∴OC=r;
因此这三个圆的半径为:OC=r,OB=r,OA=r.
17.(1)如图1,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若AB=10,CD=8,求AE的长.
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.
解:(1)∵AB为圆O的直径,弦CD⊥AB,垂足为点E.
∴CE=CD=4.
在直角△OCE中,OE===3.
则AE=OA﹣OE=5﹣3=2;
(2)如图,过点P作PE⊥OB于E,
∵PC∥OA,
∴∠AOP=∠COP,
∴∠PCE=∠BOP+∠COP=∠BOP+∠AOP=∠AOB=30°,
又∵PC=4,
∴PE=PC=×4=2,
∵∠AOP=∠BOP,PD⊥OA,
∴PD=PE=2.
18.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长.
解:连接OB,
则OB=×10=5,
∵OM⊥AB,OM过O,
∴AB=2AM=2BM,
在Rt△OMB中,由勾股定理得:BM===4,
∴AB=2BM=8.
19.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
解:(1)如图(1),∵OD⊥BC,
∴BD=BC=,
∴OD==;
(2)如图(2),存在,DE是不变的.
连接AB,则AB==2,
∵D和E分别是线段BC和AC的中点,
∴DE=AB=;
(3)如图(3),连接OC,
∵BD=x,
∴OD=,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=45°,
过D作DF⊥OE,
∴DF==,由(2)已知DE=,
∴在Rt△DEF中,EF==,
∴OE=OF+EF=+=
∴y=DF?OE=??
=(0<x<).
20.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
解:这辆卡车能通过厂门.理由如下:
如图M,N为卡车的宽度,过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
则CD=MN=1.6m,AB=2m,
由作法得,CE=DE=0.8m,
又∵OC=OA=1m,
在Rt△OCE中,OE===0.6(m),
∴CM=2.3+0.6=2.9m>2.5m.
所以这辆卡车能通过厂门.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
24.1.2
垂直于弦的直径
高频易错题集
一.选择题(共10小题)
1.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17
B.18
C.19
D.20
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的直径为( )
A.10
B.8
C.5
D.3
3.如图,直线y=﹣x+4与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为( )
A.
B.
C.
D.
4.过⊙O内一点M的最长弦为20cm,最短弦为16cm,那么OM的长为( )
A.3cm
B.6cm
C.8cm
D.9cm
5.如图,⊙O经过菱形ABCO的顶点A、B、C,若OP⊥AB交⊙O于点P,则∠PAB的大小为( )
A.15°
B.20°
C.25°
D.30°
6.如图,在⊙O中,C为弦AB上一点,AC=2,BC=6,⊙O的半径为5,则OC=( )
A.
B.4
C.3
D.
7.如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
8.下列命题中,不正确的是( )
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弧
9.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有( )
A.1组
B.2组
C.3组
D.4组
10.下列命题中,正确的是( )
A.垂直于弦的直径平分弦,并且平分弦所对的弧
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.AB,CD是⊙O的弦,若AB=CD,则AB∥CD
D.圆是轴对称图形,对称轴是圆的每一条直径
二.填空题(共5小题)
11.如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是
.
12.如图,⊙O的直径CD=20,AB是⊙O的弦,且AB⊥CD,垂足为M,若CM=4,则AB的长为
.
13.如图,弦AB⊥直径CD于E,若AB=10,CE=1,则CD=
.
14.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为
.
15.如图,圆内一条弦CD与直径AB相交成30°角,且分直径成1cm和5cm两部分,则这条弦的弦心距是
.
三.解答题(共5小题)
16.如图,以点O为圆心的三个同心圆把以OD为半径的大圆O的面积四等分,若OD=r,求这三个圆的半径OA、OB、OC的长(用含r的式子表示).
17.(1)如图1,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若AB=10,CD=8,求AE的长.
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.
18.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长.
19.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
20.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
试题解析
一.选择题(共10小题)
1.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17
B.18
C.19
D.20
解:连接OP,OQ,分别交AC,BC于H,I,
∵M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q,
∴OP⊥AC,OQ⊥BC,由对称性可知:H,P,M三点共线,I,Q,N三点共线,
∴H、I是AC、BC的中点,
∴OH+OI=(AC+BC)=13,
∵MH+NI=AC+BC=13,MP+NQ=7,
∴PH+QI=13﹣7=6,
∴AB=OP+OQ=OH+OI+PH+QI=13+6=19,
故选:C.
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的直径为( )
A.10
B.8
C.5
D.3
解:连接OC,
∵CD⊥AB,CD=8,
∴PC=CD=×8=4,
在Rt△OCP中,设OC=x,则OA=x,
∵PC=4,OP=AP﹣OA=8﹣x,
∴OC2=PC2+OP2,
即x2=42+(8﹣x)2,
解得x=5,
∴⊙O的直径为10.
故选:A.
3.如图,直线y=﹣x+4与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为( )
A.
B.
C.
D.
解:连接AO,并延长交直线CD于G,连接AQ,
∵Q是MN的中点.
∴AQ⊥MN,
∵A的坐标为(﹣4,﹣4),
∴直线AO:y=x,AO=4,
∵直线CD:y=﹣x+4,
∴AO⊥CD,
∴∠AQO=∠OGP=90°,
∵∠AOQ=∠POG,
∴∠AOQ∽△POG,
∴,
当x=0时,y=4,当y=0时,x=4,
∴OC=OD=4,
∴OG=CD=2,
∵OP=t,OQ=S,
∴,
S=,
故选项C、D不正确;
当OP=2时,即S=OQ=4,t=2,直线OP过圆心A,此时Q与A重合,此种情况成立,
故选项B不正确;
故选:A.
4.过⊙O内一点M的最长弦为20cm,最短弦为16cm,那么OM的长为( )
A.3cm
B.6cm
C.8cm
D.9cm
解:由题意知,最长的弦为直径,最短的弦为垂直于直径的弦,
如图所示.直径ED⊥AB于点M,
则ED=20cm,AB=16cm,
由垂径定理知:点M为AB中点,
∴AM=8cm,
∵半径OA=10cm,
∴OM2=OA2﹣AM2=100﹣64=6,
∴OM=6cm.
故选:B.
5.如图,⊙O经过菱形ABCO的顶点A、B、C,若OP⊥AB交⊙O于点P,则∠PAB的大小为( )
A.15°
B.20°
C.25°
D.30°
解:连接OB,
∵四边形ABCO是菱形,
∴OA=AB,
∵OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∵OP⊥AB,
∴∠BOP=∠AOB=30°,
由圆周角定理得,∠PAB=∠BOP=15°,
故选:A.
6.如图,在⊙O中,C为弦AB上一点,AC=2,BC=6,⊙O的半径为5,则OC=( )
A.
B.4
C.3
D.
解:设OC=x,利用圆内相交弦定理可得:2×6=(5﹣x)(5+x)
解得x=.
故选:A.
7.如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
解:作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
由垂径定理、勾股定理得:OM=ON==3,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=3
故选:C.
8.下列命题中,不正确的是( )
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弧
解:A、根据垂径定理的推论可知,垂直平分弦的直线经过圆心;故本答案正确.
B、直径是最长的弦,任意两条直径互相平分,但不一定互相垂直,故被平分的弦不能是直径;故本答案错误.
C、如图所示,两弦平行,则圆周角相等,圆周角相等,则弧相等;故本选项正确.
D、根据垂径定理可知,垂直于弦的直径必平分弦所对的弧;故本选项正确.
故选:B.
9.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有( )
A.1组
B.2组
C.3组
D.4组
解:由垂径定理知,点H是AB的中点,也是CD的中点,则有CH=HD,AH=HB,所以AD=BC,AC=BD.
所以共有4组相等的线段.
故选:D.
10.下列命题中,正确的是( )
A.垂直于弦的直径平分弦,并且平分弦所对的弧
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.AB,CD是⊙O的弦,若AB=CD,则AB∥CD
D.圆是轴对称图形,对称轴是圆的每一条直径
解:A、垂直于弦的直径平分弦,且平分弦所对的弧,故本选项正确;
B、平分弦(弦不是直径)直径垂直于弦,并且平分弦所对的弧,故本选项错误;
C、AB和CD可能相交,故本选项错误;
D、圆是轴对称图形,对称轴是圆的每一条直径所在的直线,故本选项错误;
故选:A.
二.填空题(共5小题)
11.如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是 .
解:连接OA,
∵C是AB的中点,
∴AC=AB=2,OC⊥AB,
∴OA2=OC2+AC2,即OA2=(OA﹣1)2+22,
解得,OA=,
故答案为:.
12.如图,⊙O的直径CD=20,AB是⊙O的弦,且AB⊥CD,垂足为M,若CM=4,则AB的长为 16 .
解:连接OA,
∵⊙O的直径CD=20,
∴OA=OC=10,
∵CM=4,
∴OM=10﹣4=6,
在Rt△OAM中,由勾股定理得:AM==8,
∴由垂径定理得:AB=2AM=16.
故答案为:16.
13.如图,弦AB⊥直径CD于E,若AB=10,CE=1,则CD= 26 .
解:连接OA,
∵弦AB⊥直径CD于E,
∴AE=EB=5,
设圆的半径为r,则OE=r﹣1,
由勾股定理得,r2=52+(r﹣1)2,
解得,r=13,
则CD=2r=26,
故答案为:26.
14.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为 7dm或1dm .
解:如图,AB∥CD,AB=6dm,CD=8dm,
过O点作OE⊥AB于E,交CD于F点,连OA、OC,
∴AE=BE=AB=3,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴CF=FD=CD=4,
在Rt△OAE中,OA=5dm
OE===4,
同理可得OF=3,
当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7(dm);
当圆心O不在AB与CD之间时,AB与CD的距离=OE﹣OF=4﹣3=1(dm).
故答案为7dm或1dm.
15.如图,圆内一条弦CD与直径AB相交成30°角,且分直径成1cm和5cm两部分,则这条弦的弦心距是 1cm .
解:过点O作OF⊥CD于点F,设弦CD与直径AB相交于点E,
∵分直径成1cm和5cm两部分,
∴AB=6cm,
∴OA=AB=3cm,
∴OE=OA﹣AE=2cm,
∵∠OEF=30°,
∴OF=OE=1(cm).
故答案为:1cm.
三.解答题(共5小题)
16.如图,以点O为圆心的三个同心圆把以OD为半径的大圆O的面积四等分,若OD=r,求这三个圆的半径OA、OB、OC的长(用含r的式子表示).
解:∵π?OA2=π?r2,
∴OA2=r2,
∴OA=r;
∵π?OB2=π?r2,
∴OB2=r2,
∴OB=r;
∵π?OC2=π?r2,
∴OC2=r2,
∴OC=r;
因此这三个圆的半径为:OC=r,OB=r,OA=r.
17.(1)如图1,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若AB=10,CD=8,求AE的长.
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.
解:(1)∵AB为圆O的直径,弦CD⊥AB,垂足为点E.
∴CE=CD=4.
在直角△OCE中,OE===3.
则AE=OA﹣OE=5﹣3=2;
(2)如图,过点P作PE⊥OB于E,
∵PC∥OA,
∴∠AOP=∠COP,
∴∠PCE=∠BOP+∠COP=∠BOP+∠AOP=∠AOB=30°,
又∵PC=4,
∴PE=PC=×4=2,
∵∠AOP=∠BOP,PD⊥OA,
∴PD=PE=2.
18.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长.
解:连接OB,
则OB=×10=5,
∵OM⊥AB,OM过O,
∴AB=2AM=2BM,
在Rt△OMB中,由勾股定理得:BM===4,
∴AB=2BM=8.
19.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
解:(1)如图(1),∵OD⊥BC,
∴BD=BC=,
∴OD==;
(2)如图(2),存在,DE是不变的.
连接AB,则AB==2,
∵D和E分别是线段BC和AC的中点,
∴DE=AB=;
(3)如图(3),连接OC,
∵BD=x,
∴OD=,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=45°,
过D作DF⊥OE,
∴DF==,由(2)已知DE=,
∴在Rt△DEF中,EF==,
∴OE=OF+EF=+=
∴y=DF?OE=??
=(0<x<).
20.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
解:这辆卡车能通过厂门.理由如下:
如图M,N为卡车的宽度,过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
则CD=MN=1.6m,AB=2m,
由作法得,CE=DE=0.8m,
又∵OC=OA=1m,
在Rt△OCE中,OE===0.6(m),
∴CM=2.3+0.6=2.9m>2.5m.
所以这辆卡车能通过厂门.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
