24.2.1 点和圆的位置关系 高频易错题集 (原卷+解析)
文档属性
| 名称 | 24.2.1 点和圆的位置关系 高频易错题集 (原卷+解析) |  | |
| 格式 | zip | ||
| 文件大小 | 403.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 11:17:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.2.1
点和圆的位置关系
高频易错题集
一.选择题(共10小题)
1.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2﹣
2.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上
B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外
D.当﹣1<a<3时,点B在圆A内
3.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有( )
A.1
个
B.2个
C.3个
D.4
个
4.下列有关圆的一些结论①任意三点可以确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦,并且平分弦所对的弧;④圆内接四边形对角互补.其中正确的结论是( )
A.①
B.②
C.③
D.④
5.下列命题是假命题的是( )
A.三角形的外心到三角形三个顶点的距离相等
B.将一次函数y=3x﹣1的图象向上平移2个单位,所得直线不经过第四象限
C.若某等腰三角形的两边长为2和5,那么这个等腰三角形的周长为9或12
D.若关于x的一元一次不等式组无解,则m的范围是m≤1
6.对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α
B.∠α=90°,∠α的补角∠β=90°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α
D.两个角互为邻补角
7.牛顿曾说过:“反证法是数学家最精良的武器之一.”那么我们用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”时,第一步先假设( )
A.三角形中有一个内角小于60°
B.三角形中有一个内角大于60°
C.三角形中每个内角都大于60°
D.三角形中没有一个内角小于60°
8.下列说法正确的个数( )
①近似数32.6×102精确到十分位:
②在,,﹣||中,最小的数是
③如图所示,在数轴上点P所表示的数为﹣1+
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”
⑤如图②,在△ABC内一点P到这三条边的距离相等,则点P是三个角平分线的交点
A.1
B.2
C.3
D.4
9.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
A.有一个内角小于90°
B.每一个内角都大于90°
C.有一个内角小于或等于90°
D.每一个内角都小于90°
10.已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①②
B.③④②①
C.①②③④
D.③④①②
二.填空题(共5小题)
11.若⊙A的半径为5,点A的坐标为(3,4),则原点O与⊙A的位置关系是
.
12.如图,⊙O是△ABC的外接圆,若∠ACO=40°,则∠B的度数为
.
13.已知△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣1,﹣3),C(3,﹣3)则△ABC外接圆半径的长度为
.
14.用反证法证明:“如果两条直线都和第三条直线平行,那么这两条直线也互相平行”.第一步应假设:
.
15.用反证法证明“已知,在Rt△ABC中,∠C=90°,∠A≠45°.求证:AC≠BC”.第一步应先假设
.
三.解答题(共5小题)
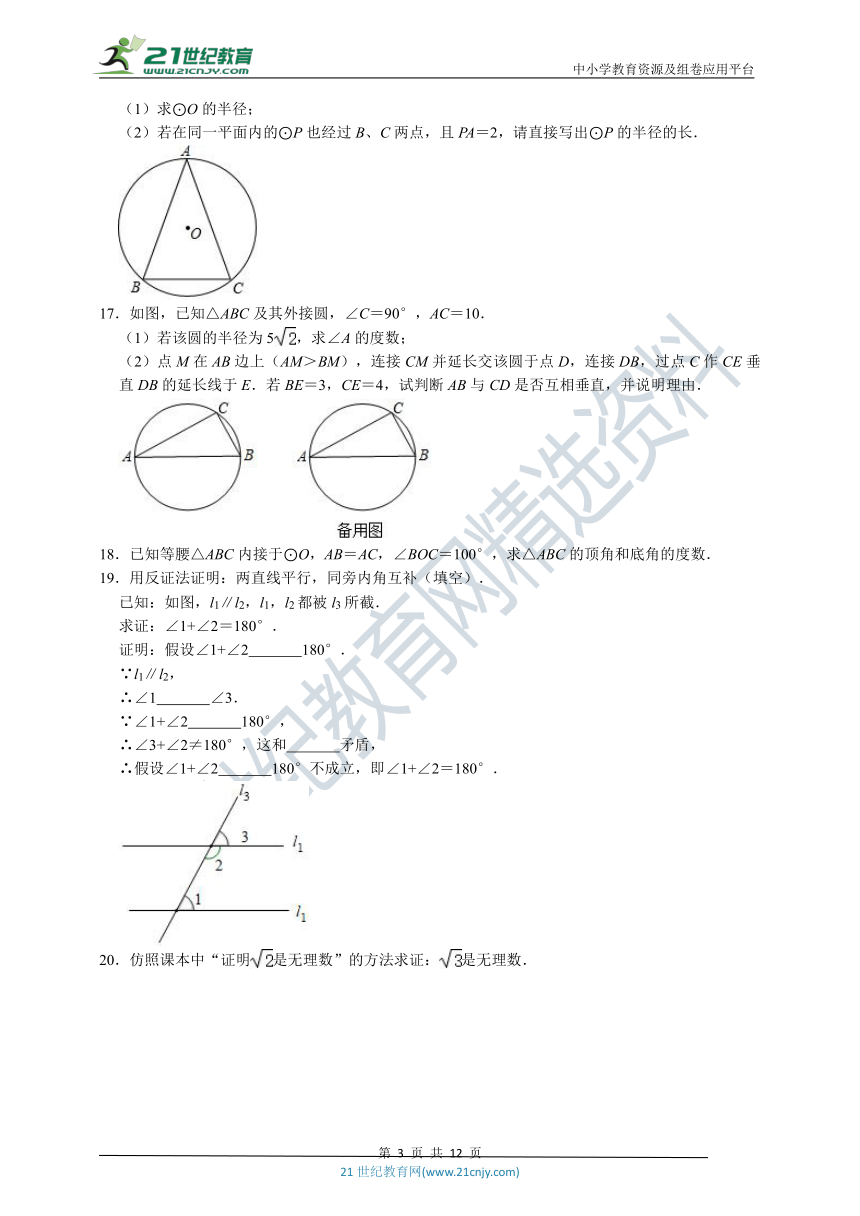
16.如图,在△ABC中,AB=AC=2,BC=4,⊙O是△ABC的外接圆.
(1)求⊙O的半径;
(2)若在同一平面内的⊙P也经过B、C两点,且PA=2,请直接写出⊙P的半径的长.
17.如图,已知△ABC及其外接圆,∠C=90°,AC=10.
(1)若该圆的半径为5,求∠A的度数;
(2)点M在AB边上(AM>BM),连接CM并延长交该圆于点D,连接DB,过点C作CE垂直DB的延长线于E.若BE=3,CE=4,试判断AB与CD是否互相垂直,并说明理由.
18.已知等腰△ABC内接于⊙O,AB=AC,∠BOC=100°,求△ABC的顶角和底角的度数.
19.用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,l1∥l2,l1,l2都被l3所截.
求证:∠1+∠2=180°.
证明:假设∠1+∠2
180°.
∵l1∥l2,
∴∠1
∠3.
∵∠1+∠2
180°,
∴∠3+∠2≠180°,这和
矛盾,
∴假设∠1+∠2
180°不成立,即∠1+∠2=180°.
20.仿照课本中“证明是无理数”的方法求证:是无理数.
试题解析
一.选择题(共10小题)
1.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2﹣
解:如图,
∵点C为坐标平面内一点,BC=1,
∴C在⊙B上,且半径为1,
取OD=OA=2,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=2,∠BOD=90°,
∴BD=2,
∴CD=2+1,
∴OM=CD=,即OM的最大值为+;
故选:B.
2.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上
B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外
D.当﹣1<a<3时,点B在圆A内
解:如图:
∵A(1,0),⊙A的半径是2,
∴AC=AE=2,
∴OE=1,OC=3,
A、当a=﹣1时,点B在E上,即B在⊙A上,正确,故本选项不合题意;
B、当a=﹣3时,B在⊙A外,即说当a<1时,点B在圆A内错误,故本选项符合题意;
C、当a<﹣1时,AB>2,即说点B在圆A外正确,故本选项不合题意;
D、当﹣1<a<3时,B在⊙A内正确,故本选项不合题意;
故选:B.
3.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有( )
A.1
个
B.2个
C.3个
D.4
个
解:∵点A、B、C在同一条直线上,
∴经过点A、B、D,或点A、C、D,或点B、C、D分别能画一个圆,
故选:C.
4.下列有关圆的一些结论①任意三点可以确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦,并且平分弦所对的弧;④圆内接四边形对角互补.其中正确的结论是( )
A.①
B.②
C.③
D.④
解:①不共线的三点确定一个圆,故①表述不正确;
①在同圆或等圆中,相等的圆心角所对的弧相等,故②表述不正确;
②平分弦(不是直径)的直径垂直于弦,故③表述不正确;
⑤圆内接四边形对角互补,故④表述正确.
故选:D.
5.下列命题是假命题的是( )
A.三角形的外心到三角形三个顶点的距离相等
B.将一次函数y=3x﹣1的图象向上平移2个单位,所得直线不经过第四象限
C.若某等腰三角形的两边长为2和5,那么这个等腰三角形的周长为9或12
D.若关于x的一元一次不等式组无解,则m的范围是m≤1
解:A、三角形的外心是三角形三边垂直平分线的交点,则三角形的外心到三角形三个顶点的距离相等,本选项说法是真命题;
B、将一次函数y=3x﹣1的图象向上平移2个单位,得到y=3x+1,图象经过第一、二、三象限,不经过第四象限,本选项说法是真命题;
C、若某等腰三角形的两边长为2和5,那么这个等腰三角形的周长为12,本选项说法是假命题;
D、关于x的一元一次不等式组的解集是1<x≤m,当m≤1时,不等式组无解,本选项说法是真命题;
故选:C.
6.对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α
B.∠α=90°,∠α的补角∠β=90°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α
D.两个角互为邻补角
解:举反例应该是证明原命题不正确,即要举出不符合叙述的情况;
A、∠α的补角∠β>∠α,符合假命题的结论,故A错误;
B、∠α的补角∠β=∠α,符合假命题的结论,故B错误;
C、∠α的补角∠β<∠α,与假命题结论相反,故C正确;
D、由于无法说明两角具体的大小关系,故D错误.
故选:C.
7.牛顿曾说过:“反证法是数学家最精良的武器之一.”那么我们用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”时,第一步先假设( )
A.三角形中有一个内角小于60°
B.三角形中有一个内角大于60°
C.三角形中每个内角都大于60°
D.三角形中没有一个内角小于60°
解:用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”时,
第一步先假设三角形中每个内角都大于60°,
故选:C.
8.下列说法正确的个数( )
①近似数32.6×102精确到十分位:
②在,,﹣||中,最小的数是
③如图所示,在数轴上点P所表示的数为﹣1+
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”
⑤如图②,在△ABC内一点P到这三条边的距离相等,则点P是三个角平分线的交点
A.1
B.2
C.3
D.4
解:①近似数32.6×102精确到十位,故本说法错误;
②在,,﹣||中,最小的数是﹣(﹣2)2,故本说法错误;
③如图所示,在数轴上点P所表示的数为﹣1﹣,故本说法错误;
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中至少有两个钝角”,故本说法错误;
⑤如图②,在△ABC内一点P到这三条边的距离相等,则点P是三个角平分线的交点,故本说法正确;
故选:A.
9.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
A.有一个内角小于90°
B.每一个内角都大于90°
C.有一个内角小于或等于90°
D.每一个内角都小于90°
解:反证法证明“四边形中至少有一个内角大于或等于90°”时,
假设每一个内角都小于90°,
故选:D.
10.已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①②
B.③④②①
C.①②③④
D.③④①②
解:运用反证法证明这个命题的四个步骤:1、假设在△ABC中,∠B≥90°,
2、由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°,
3、∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾,
4、因此假设不成立.∴∠B<90°,
故选:D.
二.填空题(共5小题)
11.若⊙A的半径为5,点A的坐标为(3,4),则原点O与⊙A的位置关系是 在圆上 .
解:∵点A的坐标为A(3,4),
∴OA==5,
∴根据点到圆心的距离等于半径,则知点在圆上.
故答案为:在圆上.
12.如图,⊙O是△ABC的外接圆,若∠ACO=40°,则∠B的度数为 50° .
解:连接OA,如图,
∵∠ACO=40°,OA=OC,
∴∠CAO=∠ACO=40°,
∴∠AOC=100°,
∴∠B=50°.
故答案为:50°.
13.已知△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣1,﹣3),C(3,﹣3)则△ABC外接圆半径的长度为 .
解:设△ABC的外心为M,如图:
∵A(﹣1,3),B(﹣1,﹣3),C(3,﹣3),
∴AB、BC的垂直平分线过(1,0),故M(1,0);
MA就是⊙M的半径长,
由勾股定理得:MA==,
即△ABC的外接圆半径为.
故答案为:.
14.用反证法证明:“如果两条直线都和第三条直线平行,那么这两条直线也互相平行”.第一步应假设: 这两条直线不平行 .
解:用反证法证明:“如果两条直线都和第三条直线平行,那么这两条直线也互相平行”
第一步应假设:这两条直线不平行,
故答案为:这两条直线不平行.
15.用反证法证明“已知,在Rt△ABC中,∠C=90°,∠A≠45°.求证:AC≠BC”.第一步应先假设 AC=BC .
解:用反证法证明“已知,在Rt△ABC中,∠C=90°,∠A≠45°.求证:AC≠BC”.
第一步应先假设AC=BC,
故答案为:AC=BC.
三.解答题(共5小题)
16.如图,在△ABC中,AB=AC=2,BC=4,⊙O是△ABC的外接圆.
(1)求⊙O的半径;
(2)若在同一平面内的⊙P也经过B、C两点,且PA=2,请直接写出⊙P的半径的长.
解:(1)过点A作AD⊥BC,垂足为D,连接OB、OC,
∵AB=AC,AD⊥BC,
∴AD垂直平分BC,
∵OB=OC,
∴点O在BC的垂直平分线上,即O在AD上,
∵BC=4,
∴BD=BC=2,
∵在Rt△ABD中,∠ADB=90°,AB=2,
∴AD==6,
设OA=OB=r,则OD=6﹣r.
∵在Rt△OBD中,∠ODB=90°,
∴OD2+BD2=OB2,即(6﹣r)2+22=r2.
解得r=,
即⊙O的半径为,
(2)当⊙P也经过B、C两点,
则设PB=r,
PA=2,则PD=6﹣2=4或6+2=8,
BD=2,
∴PB==2
或PB==2.
所以⊙P的半径的长为2或2.
17.如图,已知△ABC及其外接圆,∠C=90°,AC=10.
(1)若该圆的半径为5,求∠A的度数;
(2)点M在AB边上(AM>BM),连接CM并延长交该圆于点D,连接DB,过点C作CE垂直DB的延长线于E.若BE=3,CE=4,试判断AB与CD是否互相垂直,并说明理由.
解:(1)∵∠C=90°,
∴AB为△ABC外接圆的直径,
∵该圆的半径为5,
∴AB=10,
∴在Rt△ABC中,AC2+BC2=AB2.
∵AC=10
∴102+BC2=(10)2.
∴BC=10,
∴AC=BC.
∴∠A=∠B.
∴∠A==45°;
(2)AB与CD互相垂直,理由如下:
由(1)得,AB为直径,取AB中点O,则点O为圆心,连接OC,OD.
∵CE⊥DB,
∴∠E=90°.
∴在Rt△CBE中,BE2+CE2=BC2.
即32+42=BC2.
∴BC=5.
∵,
∴∠A=∠BOC,∠CDE=∠BOC.
∴∠A=∠CDE.
∵∠ACB=90°,
∴在Rt△ACB中,tanA===.
∴tan∠CDE=tanA=.
又∵在Rt△CED中,tan∠CDE=,
∴=.
即=.
∴DE=8.
∴BD=DE﹣BE=8﹣3=5.
∴BC=BD.
∴∠BOC=∠BOD.
∵OC=OD,
∴OM⊥CD.
即AB⊥CD.
18.已知等腰△ABC内接于⊙O,AB=AC,∠BOC=100°,求△ABC的顶角和底角的度数.
解:(1)圆心O在△ABC外部,
在优弧BC上任选一点D,连接BD,CD.
∴∠BDC=∠BOC=50°,
∴∠BAC=180°﹣∠BDC=130°;
∵AB=AC,
∴∠ABC=(180°﹣∠BAC)÷2=25°;
(2)圆心O在△ABC内部.∠BAC=∠BOC=50°,
∵AB=AC,
∴∠ABC=(180°﹣∠BAC)÷2=65°.
19.用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,l1∥l2,l1,l2都被l3所截.
求证:∠1+∠2=180°.
证明:假设∠1+∠2 ≠ 180°.
∵l1∥l2,
∴∠1 = ∠3.
∵∠1+∠2 ≠ 180°,
∴∠3+∠2≠180°,这和 平角为180° 矛盾,
∴假设∠1+∠2 ≠ 180°不成立,即∠1+∠2=180°.
证明:假设∠1+∠2≠180°.
∵l1∥l2,
∴∠1=∠3.
∵∠1+∠2≠180°,
∴∠3+∠2≠180°,这与平角为180°矛盾,
∴假设∠1+∠2≠180°不成立,即∠1+∠2=180°.
故答案为:≠;=;≠;平角为180°;≠.
20.仿照课本中“证明是无理数”的方法求证:是无理数.
证明:假设是有理数,那么它可以表示成(p与q是互质的两个正整数).
于是()2=()2=3,
所以,q2=3p2.于是q2是3的倍数,所以q也是3的倍数,
从而可设q=3m,所以(3m)2=3p2,p2=3m2,于是可得p也是3的倍数.
这与“p与q是互质的两个正整数”矛盾.
从而可知“是有理数”的假设不成立,
所以,是无理数.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
24.2.1
点和圆的位置关系
高频易错题集
一.选择题(共10小题)
1.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2﹣
2.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上
B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外
D.当﹣1<a<3时,点B在圆A内
3.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有( )
A.1
个
B.2个
C.3个
D.4
个
4.下列有关圆的一些结论①任意三点可以确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦,并且平分弦所对的弧;④圆内接四边形对角互补.其中正确的结论是( )
A.①
B.②
C.③
D.④
5.下列命题是假命题的是( )
A.三角形的外心到三角形三个顶点的距离相等
B.将一次函数y=3x﹣1的图象向上平移2个单位,所得直线不经过第四象限
C.若某等腰三角形的两边长为2和5,那么这个等腰三角形的周长为9或12
D.若关于x的一元一次不等式组无解,则m的范围是m≤1
6.对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α
B.∠α=90°,∠α的补角∠β=90°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α
D.两个角互为邻补角
7.牛顿曾说过:“反证法是数学家最精良的武器之一.”那么我们用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”时,第一步先假设( )
A.三角形中有一个内角小于60°
B.三角形中有一个内角大于60°
C.三角形中每个内角都大于60°
D.三角形中没有一个内角小于60°
8.下列说法正确的个数( )
①近似数32.6×102精确到十分位:
②在,,﹣||中,最小的数是
③如图所示,在数轴上点P所表示的数为﹣1+
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”
⑤如图②,在△ABC内一点P到这三条边的距离相等,则点P是三个角平分线的交点
A.1
B.2
C.3
D.4
9.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
A.有一个内角小于90°
B.每一个内角都大于90°
C.有一个内角小于或等于90°
D.每一个内角都小于90°
10.已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①②
B.③④②①
C.①②③④
D.③④①②
二.填空题(共5小题)
11.若⊙A的半径为5,点A的坐标为(3,4),则原点O与⊙A的位置关系是
.
12.如图,⊙O是△ABC的外接圆,若∠ACO=40°,则∠B的度数为
.
13.已知△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣1,﹣3),C(3,﹣3)则△ABC外接圆半径的长度为
.
14.用反证法证明:“如果两条直线都和第三条直线平行,那么这两条直线也互相平行”.第一步应假设:
.
15.用反证法证明“已知,在Rt△ABC中,∠C=90°,∠A≠45°.求证:AC≠BC”.第一步应先假设
.
三.解答题(共5小题)
16.如图,在△ABC中,AB=AC=2,BC=4,⊙O是△ABC的外接圆.
(1)求⊙O的半径;
(2)若在同一平面内的⊙P也经过B、C两点,且PA=2,请直接写出⊙P的半径的长.
17.如图,已知△ABC及其外接圆,∠C=90°,AC=10.
(1)若该圆的半径为5,求∠A的度数;
(2)点M在AB边上(AM>BM),连接CM并延长交该圆于点D,连接DB,过点C作CE垂直DB的延长线于E.若BE=3,CE=4,试判断AB与CD是否互相垂直,并说明理由.
18.已知等腰△ABC内接于⊙O,AB=AC,∠BOC=100°,求△ABC的顶角和底角的度数.
19.用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,l1∥l2,l1,l2都被l3所截.
求证:∠1+∠2=180°.
证明:假设∠1+∠2
180°.
∵l1∥l2,
∴∠1
∠3.
∵∠1+∠2
180°,
∴∠3+∠2≠180°,这和
矛盾,
∴假设∠1+∠2
180°不成立,即∠1+∠2=180°.
20.仿照课本中“证明是无理数”的方法求证:是无理数.
试题解析
一.选择题(共10小题)
1.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2﹣
解:如图,
∵点C为坐标平面内一点,BC=1,
∴C在⊙B上,且半径为1,
取OD=OA=2,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=2,∠BOD=90°,
∴BD=2,
∴CD=2+1,
∴OM=CD=,即OM的最大值为+;
故选:B.
2.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上
B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外
D.当﹣1<a<3时,点B在圆A内
解:如图:
∵A(1,0),⊙A的半径是2,
∴AC=AE=2,
∴OE=1,OC=3,
A、当a=﹣1时,点B在E上,即B在⊙A上,正确,故本选项不合题意;
B、当a=﹣3时,B在⊙A外,即说当a<1时,点B在圆A内错误,故本选项符合题意;
C、当a<﹣1时,AB>2,即说点B在圆A外正确,故本选项不合题意;
D、当﹣1<a<3时,B在⊙A内正确,故本选项不合题意;
故选:B.
3.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有( )
A.1
个
B.2个
C.3个
D.4
个
解:∵点A、B、C在同一条直线上,
∴经过点A、B、D,或点A、C、D,或点B、C、D分别能画一个圆,
故选:C.
4.下列有关圆的一些结论①任意三点可以确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦,并且平分弦所对的弧;④圆内接四边形对角互补.其中正确的结论是( )
A.①
B.②
C.③
D.④
解:①不共线的三点确定一个圆,故①表述不正确;
①在同圆或等圆中,相等的圆心角所对的弧相等,故②表述不正确;
②平分弦(不是直径)的直径垂直于弦,故③表述不正确;
⑤圆内接四边形对角互补,故④表述正确.
故选:D.
5.下列命题是假命题的是( )
A.三角形的外心到三角形三个顶点的距离相等
B.将一次函数y=3x﹣1的图象向上平移2个单位,所得直线不经过第四象限
C.若某等腰三角形的两边长为2和5,那么这个等腰三角形的周长为9或12
D.若关于x的一元一次不等式组无解,则m的范围是m≤1
解:A、三角形的外心是三角形三边垂直平分线的交点,则三角形的外心到三角形三个顶点的距离相等,本选项说法是真命题;
B、将一次函数y=3x﹣1的图象向上平移2个单位,得到y=3x+1,图象经过第一、二、三象限,不经过第四象限,本选项说法是真命题;
C、若某等腰三角形的两边长为2和5,那么这个等腰三角形的周长为12,本选项说法是假命题;
D、关于x的一元一次不等式组的解集是1<x≤m,当m≤1时,不等式组无解,本选项说法是真命题;
故选:C.
6.对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α
B.∠α=90°,∠α的补角∠β=90°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α
D.两个角互为邻补角
解:举反例应该是证明原命题不正确,即要举出不符合叙述的情况;
A、∠α的补角∠β>∠α,符合假命题的结论,故A错误;
B、∠α的补角∠β=∠α,符合假命题的结论,故B错误;
C、∠α的补角∠β<∠α,与假命题结论相反,故C正确;
D、由于无法说明两角具体的大小关系,故D错误.
故选:C.
7.牛顿曾说过:“反证法是数学家最精良的武器之一.”那么我们用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”时,第一步先假设( )
A.三角形中有一个内角小于60°
B.三角形中有一个内角大于60°
C.三角形中每个内角都大于60°
D.三角形中没有一个内角小于60°
解:用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”时,
第一步先假设三角形中每个内角都大于60°,
故选:C.
8.下列说法正确的个数( )
①近似数32.6×102精确到十分位:
②在,,﹣||中,最小的数是
③如图所示,在数轴上点P所表示的数为﹣1+
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”
⑤如图②,在△ABC内一点P到这三条边的距离相等,则点P是三个角平分线的交点
A.1
B.2
C.3
D.4
解:①近似数32.6×102精确到十位,故本说法错误;
②在,,﹣||中,最小的数是﹣(﹣2)2,故本说法错误;
③如图所示,在数轴上点P所表示的数为﹣1﹣,故本说法错误;
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中至少有两个钝角”,故本说法错误;
⑤如图②,在△ABC内一点P到这三条边的距离相等,则点P是三个角平分线的交点,故本说法正确;
故选:A.
9.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
A.有一个内角小于90°
B.每一个内角都大于90°
C.有一个内角小于或等于90°
D.每一个内角都小于90°
解:反证法证明“四边形中至少有一个内角大于或等于90°”时,
假设每一个内角都小于90°,
故选:D.
10.已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①②
B.③④②①
C.①②③④
D.③④①②
解:运用反证法证明这个命题的四个步骤:1、假设在△ABC中,∠B≥90°,
2、由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°,
3、∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾,
4、因此假设不成立.∴∠B<90°,
故选:D.
二.填空题(共5小题)
11.若⊙A的半径为5,点A的坐标为(3,4),则原点O与⊙A的位置关系是 在圆上 .
解:∵点A的坐标为A(3,4),
∴OA==5,
∴根据点到圆心的距离等于半径,则知点在圆上.
故答案为:在圆上.
12.如图,⊙O是△ABC的外接圆,若∠ACO=40°,则∠B的度数为 50° .
解:连接OA,如图,
∵∠ACO=40°,OA=OC,
∴∠CAO=∠ACO=40°,
∴∠AOC=100°,
∴∠B=50°.
故答案为:50°.
13.已知△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣1,﹣3),C(3,﹣3)则△ABC外接圆半径的长度为 .
解:设△ABC的外心为M,如图:
∵A(﹣1,3),B(﹣1,﹣3),C(3,﹣3),
∴AB、BC的垂直平分线过(1,0),故M(1,0);
MA就是⊙M的半径长,
由勾股定理得:MA==,
即△ABC的外接圆半径为.
故答案为:.
14.用反证法证明:“如果两条直线都和第三条直线平行,那么这两条直线也互相平行”.第一步应假设: 这两条直线不平行 .
解:用反证法证明:“如果两条直线都和第三条直线平行,那么这两条直线也互相平行”
第一步应假设:这两条直线不平行,
故答案为:这两条直线不平行.
15.用反证法证明“已知,在Rt△ABC中,∠C=90°,∠A≠45°.求证:AC≠BC”.第一步应先假设 AC=BC .
解:用反证法证明“已知,在Rt△ABC中,∠C=90°,∠A≠45°.求证:AC≠BC”.
第一步应先假设AC=BC,
故答案为:AC=BC.
三.解答题(共5小题)
16.如图,在△ABC中,AB=AC=2,BC=4,⊙O是△ABC的外接圆.
(1)求⊙O的半径;
(2)若在同一平面内的⊙P也经过B、C两点,且PA=2,请直接写出⊙P的半径的长.
解:(1)过点A作AD⊥BC,垂足为D,连接OB、OC,
∵AB=AC,AD⊥BC,
∴AD垂直平分BC,
∵OB=OC,
∴点O在BC的垂直平分线上,即O在AD上,
∵BC=4,
∴BD=BC=2,
∵在Rt△ABD中,∠ADB=90°,AB=2,
∴AD==6,
设OA=OB=r,则OD=6﹣r.
∵在Rt△OBD中,∠ODB=90°,
∴OD2+BD2=OB2,即(6﹣r)2+22=r2.
解得r=,
即⊙O的半径为,
(2)当⊙P也经过B、C两点,
则设PB=r,
PA=2,则PD=6﹣2=4或6+2=8,
BD=2,
∴PB==2
或PB==2.
所以⊙P的半径的长为2或2.
17.如图,已知△ABC及其外接圆,∠C=90°,AC=10.
(1)若该圆的半径为5,求∠A的度数;
(2)点M在AB边上(AM>BM),连接CM并延长交该圆于点D,连接DB,过点C作CE垂直DB的延长线于E.若BE=3,CE=4,试判断AB与CD是否互相垂直,并说明理由.
解:(1)∵∠C=90°,
∴AB为△ABC外接圆的直径,
∵该圆的半径为5,
∴AB=10,
∴在Rt△ABC中,AC2+BC2=AB2.
∵AC=10
∴102+BC2=(10)2.
∴BC=10,
∴AC=BC.
∴∠A=∠B.
∴∠A==45°;
(2)AB与CD互相垂直,理由如下:
由(1)得,AB为直径,取AB中点O,则点O为圆心,连接OC,OD.
∵CE⊥DB,
∴∠E=90°.
∴在Rt△CBE中,BE2+CE2=BC2.
即32+42=BC2.
∴BC=5.
∵,
∴∠A=∠BOC,∠CDE=∠BOC.
∴∠A=∠CDE.
∵∠ACB=90°,
∴在Rt△ACB中,tanA===.
∴tan∠CDE=tanA=.
又∵在Rt△CED中,tan∠CDE=,
∴=.
即=.
∴DE=8.
∴BD=DE﹣BE=8﹣3=5.
∴BC=BD.
∴∠BOC=∠BOD.
∵OC=OD,
∴OM⊥CD.
即AB⊥CD.
18.已知等腰△ABC内接于⊙O,AB=AC,∠BOC=100°,求△ABC的顶角和底角的度数.
解:(1)圆心O在△ABC外部,
在优弧BC上任选一点D,连接BD,CD.
∴∠BDC=∠BOC=50°,
∴∠BAC=180°﹣∠BDC=130°;
∵AB=AC,
∴∠ABC=(180°﹣∠BAC)÷2=25°;
(2)圆心O在△ABC内部.∠BAC=∠BOC=50°,
∵AB=AC,
∴∠ABC=(180°﹣∠BAC)÷2=65°.
19.用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,l1∥l2,l1,l2都被l3所截.
求证:∠1+∠2=180°.
证明:假设∠1+∠2 ≠ 180°.
∵l1∥l2,
∴∠1 = ∠3.
∵∠1+∠2 ≠ 180°,
∴∠3+∠2≠180°,这和 平角为180° 矛盾,
∴假设∠1+∠2 ≠ 180°不成立,即∠1+∠2=180°.
证明:假设∠1+∠2≠180°.
∵l1∥l2,
∴∠1=∠3.
∵∠1+∠2≠180°,
∴∠3+∠2≠180°,这与平角为180°矛盾,
∴假设∠1+∠2≠180°不成立,即∠1+∠2=180°.
故答案为:≠;=;≠;平角为180°;≠.
20.仿照课本中“证明是无理数”的方法求证:是无理数.
证明:假设是有理数,那么它可以表示成(p与q是互质的两个正整数).
于是()2=()2=3,
所以,q2=3p2.于是q2是3的倍数,所以q也是3的倍数,
从而可设q=3m,所以(3m)2=3p2,p2=3m2,于是可得p也是3的倍数.
这与“p与q是互质的两个正整数”矛盾.
从而可知“是有理数”的假设不成立,
所以,是无理数.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
