北师大版七年级上册数学 3.1字母表示数 课件(22张)
文档属性
| 名称 | 北师大版七年级上册数学 3.1字母表示数 课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 745.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览







文档简介
一只青蛙 1 张嘴,2 只眼睛 4 条腿,1 声扑通跳下水;
两只青蛙 2 张嘴,4 只眼睛 8 条腿,2 声扑通跳下水;
三只青蛙 3 张嘴,6 只眼睛12 条腿,3 声扑通跳下水;
十只青蛙__ 张嘴,__ 只眼睛__ 条腿,__ 声扑通跳下水;
…
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
…
a只青蛙_____张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
a
a
说一说
10
20
40
10
100
200
400
100
摆一摆
如图所示,搭一个正方形需要4根火柴棒.
按上面的方式,搭2个正方形需要____根火柴,
搭3个正方形需要____根火柴.
(2) 搭10个这样的正方形需要_____根火柴.
7
10
31
摆一摆
如图所示,搭一个正方形需要4根火柴棒.
(3)搭100个这样的正方形需要多少根火柴,
怎样得到的?
4+3
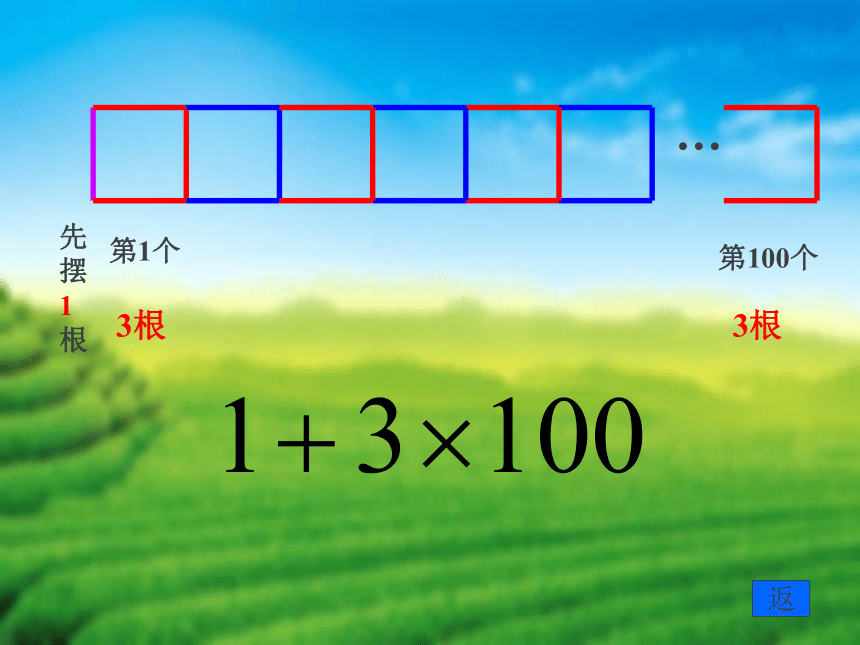
1+3
2
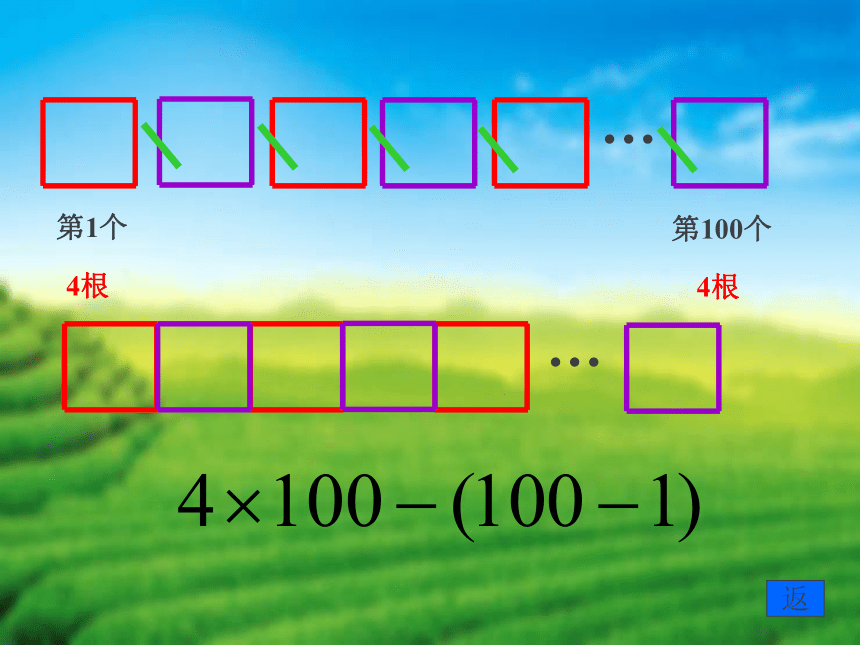
4-1
N9
…
第1个
4根
第2个
第100个
3根
3根
返
…
先摆 1根
第1个
3根
第100个
3根
返
…
第1个
2根
第2个
2根
第100个
2根
返
…
第1个
4根
第100个
4根
返
…
摆一摆
如图所示,搭一个正方形需要4根火柴棒.
(3)搭100个这样的正方形需要多少根火柴, 怎样
得到的?
(4) 如果用x表示所搭正方形的个数, 那么搭x个
这样的正方形需要多少根火柴?
4+3
1+3
2
4-1
N14
…
第1个
4根
第2个
第100个
3根
3根
返
…
先摆 1根
第1个
3根
第100个
3根
返
…
第1个
2根
第2个
2根
第100个
2根
返
…
第1个
4根
第100个
4根
返
做一做
如图所示,搭一个正方形需要4根火柴棒.
根据你的计算方法,搭200个这样的正方形需要______根火柴棒; 搭1000个这样的正方形需要_______根火柴棒; 搭1500个这样的正方形需要_______根火柴棒.
601
3001
4501
§3.1 字母能表示什么
用字母表示数, 可以把数和数量
关系简明地表示出来, 给我们研究问
题带来很大方便。
字母可以表示任何数
想一想
你能否举出一些字母表示数和数量关系的例子
1、用字母表示数的运算律
2、用字母表示公式与法则
1、在同一问题中,同一字母只能表示同一数量,不同的数量要用不同的字母表示。
2、用字母表示实际问题中某一数量时,字母的取值必须使这个问题有意义,并且符合实际。
注意:
加法结合律可以表示成___________________;
乘法交换律可以表示成________________;
乘法分配律可以表示成__________________;
加法交换律可以表示成________________;
a+b=b+a
乘法结合律可以表示成_______________;
(a+b)+c=a+(b+c)
ab=ba
a(b+c)=ab+ac
(ab)c=a(bc)
计算图形的周长和面积(用字母):
a
b
r
长方形的周长:
长方形的面积:
圆的周长:
圆的面积:
计算下列几何体的表面积和体积(用字母):
a
a
a
a
b
c
练一练
小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为_______米/秒.
如图, 用字母表示图中
阴影部分的面积是_________
m
n
p
q
3v
3. 一个三位数,个位数字是a, 十位数字是b,
百位数字是c, 这个三位数是____________
4、用棋子摆成下列一组图案:
…
( 1 )
( 2 )
( 3 )
① 填写下表:
图案编号
(1)
(2)
(3)
(4)
(5)
(10)
(100)
棋子个数
② 摆第n个图案需要____个棋子.
3
6
9
12
15
30
300
3n
本课小结:
同学们:这节课你都有那些收获?
(从知识、技能、情感价值观三方面总结)
两只青蛙 2 张嘴,4 只眼睛 8 条腿,2 声扑通跳下水;
三只青蛙 3 张嘴,6 只眼睛12 条腿,3 声扑通跳下水;
十只青蛙__ 张嘴,__ 只眼睛__ 条腿,__ 声扑通跳下水;
…
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
…
a只青蛙_____张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
a
a
说一说
10
20
40
10
100
200
400
100
摆一摆
如图所示,搭一个正方形需要4根火柴棒.
按上面的方式,搭2个正方形需要____根火柴,
搭3个正方形需要____根火柴.
(2) 搭10个这样的正方形需要_____根火柴.
7
10
31
摆一摆
如图所示,搭一个正方形需要4根火柴棒.
(3)搭100个这样的正方形需要多少根火柴,
怎样得到的?
4+3
1+3
2
4-1
N9
…
第1个
4根
第2个
第100个
3根
3根
返
…
先摆 1根
第1个
3根
第100个
3根
返
…
第1个
2根
第2个
2根
第100个
2根
返
…
第1个
4根
第100个
4根
返
…
摆一摆
如图所示,搭一个正方形需要4根火柴棒.
(3)搭100个这样的正方形需要多少根火柴, 怎样
得到的?
(4) 如果用x表示所搭正方形的个数, 那么搭x个
这样的正方形需要多少根火柴?
4+3
1+3
2
4-1
N14
…
第1个
4根
第2个
第100个
3根
3根
返
…
先摆 1根
第1个
3根
第100个
3根
返
…
第1个
2根
第2个
2根
第100个
2根
返
…
第1个
4根
第100个
4根
返
做一做
如图所示,搭一个正方形需要4根火柴棒.
根据你的计算方法,搭200个这样的正方形需要______根火柴棒; 搭1000个这样的正方形需要_______根火柴棒; 搭1500个这样的正方形需要_______根火柴棒.
601
3001
4501
§3.1 字母能表示什么
用字母表示数, 可以把数和数量
关系简明地表示出来, 给我们研究问
题带来很大方便。
字母可以表示任何数
想一想
你能否举出一些字母表示数和数量关系的例子
1、用字母表示数的运算律
2、用字母表示公式与法则
1、在同一问题中,同一字母只能表示同一数量,不同的数量要用不同的字母表示。
2、用字母表示实际问题中某一数量时,字母的取值必须使这个问题有意义,并且符合实际。
注意:
加法结合律可以表示成___________________;
乘法交换律可以表示成________________;
乘法分配律可以表示成__________________;
加法交换律可以表示成________________;
a+b=b+a
乘法结合律可以表示成_______________;
(a+b)+c=a+(b+c)
ab=ba
a(b+c)=ab+ac
(ab)c=a(bc)
计算图形的周长和面积(用字母):
a
b
r
长方形的周长:
长方形的面积:
圆的周长:
圆的面积:
计算下列几何体的表面积和体积(用字母):
a
a
a
a
b
c
练一练
小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为_______米/秒.
如图, 用字母表示图中
阴影部分的面积是_________
m
n
p
q
3v
3. 一个三位数,个位数字是a, 十位数字是b,
百位数字是c, 这个三位数是____________
4、用棋子摆成下列一组图案:
…
( 1 )
( 2 )
( 3 )
① 填写下表:
图案编号
(1)
(2)
(3)
(4)
(5)
(10)
(100)
棋子个数
② 摆第n个图案需要____个棋子.
3
6
9
12
15
30
300
3n
本课小结:
同学们:这节课你都有那些收获?
(从知识、技能、情感价值观三方面总结)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
