24.2.2 直线和圆的位置关系 高频易错题集 (原卷+解析)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 高频易错题集 (原卷+解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 563.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.2.2
直线和圆的位置关系
高频易错题集
一.选择题(共10小题)
1.圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离
B.相切
C.相交或相切
D.相离或相切
2.如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
A.0<CE≤8
B.0<CE≤5
C.3<CE≤8
D.3<CE≤5
3.⊙O的半径是3cm,圆心到直线的距离是4cm,则直线与⊙O的位置关系( )
A.相离
B.相切
C.相交
D.以上都不是
4.下列说法中,不正确的个数是( )
①直径是弦;②经过圆内一定点可以作无数条直径;③平分弦的直径垂直于弦;④过三点可以作一个圆;⑤过圆心且垂直于切线的直线必过切点.
A.1个
B.2个
C.3个
D.4个
5.如图,⊙O的半径为4,A、B、C、D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A.4
B.2
C.4
D.值不确定
6.如图,PA,PB分别与⊙O相切于点A,B,连接OP,则下列判断错误的是( )
A.∠PAO=∠PBO=90°
B.OP平分∠APB
C.PA=PB
D.∠AOB=
7.已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:
①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG.则其中正确的是( )
A.①②④
B.③④
C.①②③
D.①②③④
8.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
9.正方形ABCD中,对角线AC、BD交于O,Q为CD上任意一点,AQ交BD于M,过M作MN⊥AM交BC于N,连AN、QN.下列结论:
①MA=MN;②∠AQD=∠AQN;③S△AQN=S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.
其中正确的结论有( )
A.①②③④
B.只有①③④
C.只有②③④
D.只有①②
10.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5
B.2
C.5或2
D.2或﹣1
二.填空题(共5小题)
11.如图,⊙O的半径为7cm,直线l⊥OA,垂足为B,OB=4cm,则直线l沿直线OA平移
cm时与⊙O相切.
12.已知⊙O的面积为9πcm2,若点O到直线L的距离为πcm,则直线l与⊙O的位置关系是
.
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为
.
14.如图,P是抛物线y=x2﹣4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为
.
15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为
.
三.解答题(共5小题)
16.如图所示,AB是圆O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和圆O的位置关系,并给出证明;
(2)当CE=5,BC=8时,求圆O的半径.
17.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.
求证:∠ACB为定值.
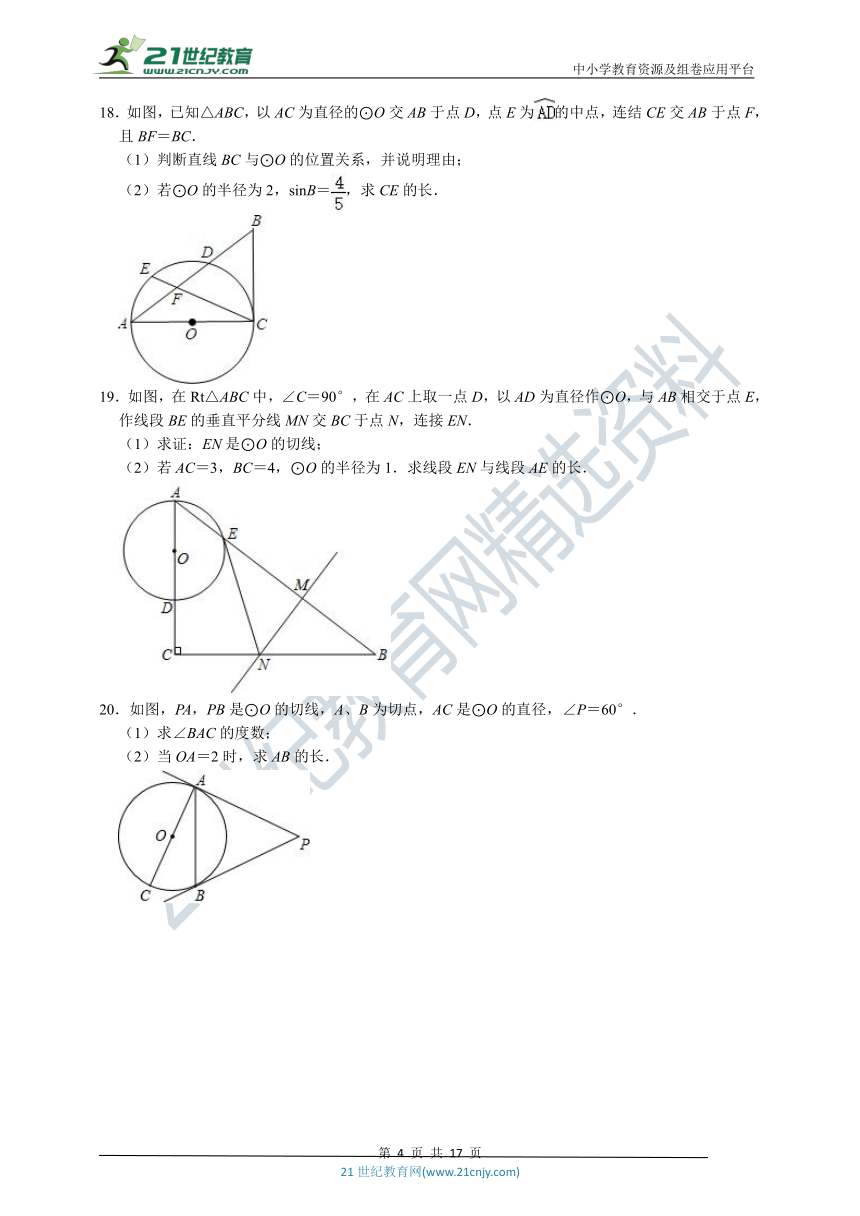
18.如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为的中点,连结CE交AB于点F,且BF=BC.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,sinB=,求CE的长.
19.如图,在Rt△ABC中,∠C=90°,在AC上取一点D,以AD为直径作⊙O,与AB相交于点E,作线段BE的垂直平分线MN交BC于点N,连接EN.
(1)求证:EN是⊙O的切线;
(2)若AC=3,BC=4,⊙O的半径为1.求线段EN与线段AE的长.
20.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
试题解析
一.选择题(共10小题)
1.圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离
B.相切
C.相交或相切
D.相离或相切
解:∵圆的半径为5cm,圆心与直线上某一点的距离为5cm,
∴直线与圆有交点
∴当圆心与该点的连线垂直于该直线时,由切线的判定定理可知,直线与圆相切;
当圆心与该点的连线不垂直于该直线时,则由垂线段最短,
可知圆心到该直线的距离小于5,从而直线与圆相交.
故选:C.
2.如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
A.0<CE≤8
B.0<CE≤5
C.3<CE≤8
D.3<CE≤5
解:如图,过A作AM⊥BC于N,CN⊥AD于N,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=5,
∴AM=CN,
∵AB=5,cosB=,
∴BM=4,
∵BC=8,
∴CM=4=BC,
∵AM⊥BC,
∴AC=AB=5,
由勾股定理得:AM=CN==3,
∴当以CE为半径的圆C与边AD有两个交点时,半径CE的取值范围是3<CE≤5,
故选:D.
3.⊙O的半径是3cm,圆心到直线的距离是4cm,则直线与⊙O的位置关系( )
A.相离
B.相切
C.相交
D.以上都不是
解:∵⊙O的半径是3cm,圆心到直线的距离是4cm,
∴4>3,
∴直线与⊙O的位置关系是相离,
故选:A.
4.下列说法中,不正确的个数是( )
①直径是弦;②经过圆内一定点可以作无数条直径;③平分弦的直径垂直于弦;④过三点可以作一个圆;⑤过圆心且垂直于切线的直线必过切点.
A.1个
B.2个
C.3个
D.4个
解:①直径是特殊的弦.所以①正确,不符合题意;
②经过圆心可以作无数条直径.所以②不正确,符合题意;
③平分弦(不是直径)的直径垂直于弦.所以③不正确,符合题意;
④过不在同一条直线上的三点可以作一个圆.所以④不正确,符合题意;
⑤过圆心且垂直于切线的直线必过切点.所以⑤正确,不符合题意.
故选:C.
5.如图,⊙O的半径为4,A、B、C、D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A.4
B.2
C.4
D.值不确定
解:当∠ADG=∠BCH=30°时,PE+PF是定值.
理由:连接OA、OB、OC、OD,如图:
∵DG与⊙O相切,
∴∠GDA=∠ABD.
∵∠ADG=30°,
∴∠ABD=30°.
∴∠AOD=2∠ABD=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA.
∴=,=.
∴+=+=1.
∴+=1.
∴PE+PF=4.
∴当∠ADG=∠BCH=30°时,PE+PF=4.
故选:A.
6.如图,PA,PB分别与⊙O相切于点A,B,连接OP,则下列判断错误的是( )
A.∠PAO=∠PBO=90°
B.OP平分∠APB
C.PA=PB
D.∠AOB=
解:∵PA,PB分别与⊙O相切于点A,B,
∴∠PAO=∠PBO=90°,OP平分∠APB,PA=PB,
则A、B、C正确,不符合题意;
∠AOB的度数与的度数相等,D错误,符合题意;
故选:D.
7.已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:
①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG.则其中正确的是( )
A.①②④
B.③④
C.①②③
D.①②③④
解:连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,
∵OD=OB,
∴∠ABD=∠ODB,
∵∠AOD=∠OBD+∠ODB=2∠OBD,
∵∠AOD=2∠ABC,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
∵AB是直径,
∴CD⊥AB,
∴①正确;
∵CD⊥AB,
∴∠P+∠PCD=90°,
∵OD=OC,
∴∠OCD=∠ODC=∠P,
∴∠PCD+∠OCD=90°,
∴∠PCO=90°,
∴PC是切线,∴②正确;
假设OD∥GF,则∠AOD=∠FEB=2∠ABC,
∴3∠ABC=90°,
∴∠ABC=30°,
已知没有给出∠B=30°,∴③错误;
∵AB是直径,
∴∠ACB=90°,
∵EF⊥BC,
∴AC∥EF,
∴弧CF=弧AG,
∴AG=CF,
∵OQ⊥CF,OZ⊥BG,
∴CQ=AG,OZ=AG,BZ=BG,
∴OZ=CQ,
∵OC=OB,∠OQC=∠OZB=90°,
∴△OCQ≌△BOZ,
∴OQ=BZ=BG,
∴④正确.
故选:A.
8.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选:A.
9.正方形ABCD中,对角线AC、BD交于O,Q为CD上任意一点,AQ交BD于M,过M作MN⊥AM交BC于N,连AN、QN.下列结论:
①MA=MN;②∠AQD=∠AQN;③S△AQN=S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.
其中正确的结论有( )
A.①②③④
B.只有①③④
C.只有②③④
D.只有①②
解:
延长CD到F,使DF=BN,连接AF,过A作AH⊥NQ于H,
∵正方形ABCD,NM⊥AQ,
∴∠AMN=∠ABC=90°,
∴ABNM四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴MA=MN,∴①正确;
∵正方形ABCD,
∴∠ABN=∠ADF=90°,AD=AB,
在△ABN和△ADF中
∵,
∴△ABN≌△ADF,
∴∠FAD=∠BAN,AF=AN,
∵∠NAM=∠BAC=45°,
∴∠FAQ=∠FAD+∠DAQ=45°=∠NAQ,
在△NAQ和△FAQ中
∵,
∴△NAQ≌△FAQ,
∴∠AQN=∠AQD,∴②正确;
在△ADQ和△AHQ中
∵,
∴△ADQ≌△AHQ,
∴S△ADQ=S△AQH,
∴S△NAQ=S△FAQ=S△FAD+S△ADQ=S五边形ABNQD,
∴③正确;
∵AH=AD=AB,AH⊥NQ,
∴QN是以A为圆心,以AB为半径的圆的切线,
∴④正确.
故选:A.
10.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5
B.2
C.5或2
D.2或﹣1
解:设直角三角形ABC内切圆的圆心为点I,半径为r,
三边上的切点分别为D、E、F,
连接ID、IE、IF,
得正方形,则正方形的边长即为r,
如图所示:
当BC为直角边时,
AC==10,
根据切线长定理,得
AD=AF=AB﹣BD=6﹣r,
CE=CF=BC﹣BE=8﹣r,
∴AF+FC=AC=10,
即6﹣r+8﹣r=10,解得r=2;
当BC为斜边时,
AC==2,
根据切线长定理,得
BD=BF=6﹣r,
CE=CF=2﹣r,
∴BC=BF+CF=6﹣r+2﹣r=8,
解得r=﹣1.
答:这个三角形的内切圆的半径是2或﹣1.
故选:D.
二.填空题(共5小题)
11.如图,⊙O的半径为7cm,直线l⊥OA,垂足为B,OB=4cm,则直线l沿直线OA平移 3或11 cm时与⊙O相切.
解:
延长AO交圆O于C,
当直线l平移到过A点或过C点时,直线l与圆相切,
AB=OA﹣OB=7﹣4=3,BC=OC+0B=7+4=11,
故答案为:3或11.
12.已知⊙O的面积为9πcm2,若点O到直线L的距离为πcm,则直线l与⊙O的位置关系是 相离 .
解:设⊙O的半径是rcm,
∵⊙O的面积为9πcm2,
∴πr2=9π,
∴r=3(cm),
∵点O到直线L的距离d为πcm,
∴d>r.
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为 6 .
解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO﹣∠PAB=90°﹣60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=2,
∴△PAB的周长=6.
故答案为:6.
14.如图,P是抛物线y=x2﹣4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为 (2+,1)或(2﹣,1)或(2,﹣1) .
解:当y=1时,x2﹣4x+3=1,
解得:x=2±,
∴P(2+,1)或(2﹣,1),
当y=﹣1时,x2﹣4x+3=﹣1,
解得:x1=x2=2,
∴P(2,﹣1),
则点P的坐标为:(2+,1)或(2﹣,1)或(2,﹣1).
15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 44 .
解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故答案为:44.
三.解答题(共5小题)
16.如图所示,AB是圆O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和圆O的位置关系,并给出证明;
(2)当CE=5,BC=8时,求圆O的半径.
解:(1)直线BD和⊙O相切.
证明:∵∠AEC=∠ODB,∠AEC=∠ABC,
∴∠ABC=∠ODB,
∵OD⊥BC,
∴∠DBC+∠ODB=90°,
∴∠DBC+∠ABC=90°,
∴∠DBO=90°,
∴直线BD和⊙O相切;
(2)∵OD⊥BC,BC=8,
∴BF=CF=4,
在Rt△CEF中,EF==3,
设圆O的半径为r,则OF=r﹣3,
在Rt△OBF中,OB2=OF2+BF2,即r2=(r﹣3)2+42,
解得,r=,即圆O的半径为.
17.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.
求证:∠ACB为定值.
证明:连接AM,BM,
由题意得:M是内心,
∴AM平分∠CAB,BM平分∠ABC,
∴∠CAM=∠BAM,∠CBM=∠ABM,
∴∠AMB=180°﹣∠BAM﹣∠ABM,
∴∠BAM+∠ABM=180°﹣∠AMB,
△ABC中,∠C=180°﹣(∠CAB+∠ACB)=180°﹣2∠BAM﹣2∠ABM=180°﹣2(180°﹣∠AMB)=2∠AMB﹣180°,
∵所在圆是个定圆,弦AB和半径都是定值,
∴∠AMB为定值,
∴∠ACB为定值2∠AMB﹣180°.
18.如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为的中点,连结CE交AB于点F,且BF=BC.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,sinB=,求CE的长.
(1)BC与⊙O相切
证明:连接AE,
∵AC是⊙O的直径
∴∠E=90°,
∴∠EAD+∠AFE=90°,
∵BF=BC,
∴∠BCE=∠BFC,
∵E为弧AD中点,
∴∠EAD=∠ACE,
∴∠BCE+∠ACE=90°,
∴AC⊥BC,
∵AC为直径,
∴BC是⊙O的切线.
(2)解:∵⊙O的半为2
∴AC=4,
∵sinB==,
∴AB=5,
∴BC==3,
∵BF=BC,
∴BF=3,AF=5﹣3=2,
∵∠EAD=∠ACE,∠E=∠E,
∴△AEF∽△CEA,
∴==,
∴EC=2EA,
设EA=x,EC=2x,
由勾股定理得:x2+4x2=16,
x=(负数舍去),
即CE=.
19.如图,在Rt△ABC中,∠C=90°,在AC上取一点D,以AD为直径作⊙O,与AB相交于点E,作线段BE的垂直平分线MN交BC于点N,连接EN.
(1)求证:EN是⊙O的切线;
(2)若AC=3,BC=4,⊙O的半径为1.求线段EN与线段AE的长.
解:(1)证明:如图,连接OE,
∵NM是BE的垂直平分线,
BN=EN,
∴∠B=∠NEB,
∵OA=OE
∴∠A=∠OEA,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠OEN=90°,即OE⊥EN,
∵OE是半径,
∴EN是⊙O的切线;
(2)如图,连接ON,
设EN长为x,则BN=EN=x
∵AC=3,BC=4,⊙O的半径为1,
∴CN=4﹣x,OC=AC﹣OA=3﹣1=2,
∴OE2+EN2=OC2+CN2,
∴12+x2=22+(4﹣x)2,
解得x=,
∴EN=.
连接ED,DB,设AE=y,
∵AC=3,BC=4,
∴AB=5,
∵⊙O的半径为1.
∴AD=2,
则DE2=AD2﹣AE2=22﹣y2,
∵CD=AC﹣AD=3﹣2=1,
∴DB2=CD2+BC2=17,
∵AD为直径,
∴∠AED=∠DEB=90,
∴DE2+EB2=DB2,
即22﹣y2+(5﹣y)2=17,
解得y=,
∴EN=,AE=.
20.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
解:(1)∵PA,PB是⊙O的切线,
∴AP=BP,
∵∠P=60°,
∴∠PAB=60°,
∵AC是⊙O的直径,
∴∠PAC=90°,
∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
24.2.2
直线和圆的位置关系
高频易错题集
一.选择题(共10小题)
1.圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离
B.相切
C.相交或相切
D.相离或相切
2.如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
A.0<CE≤8
B.0<CE≤5
C.3<CE≤8
D.3<CE≤5
3.⊙O的半径是3cm,圆心到直线的距离是4cm,则直线与⊙O的位置关系( )
A.相离
B.相切
C.相交
D.以上都不是
4.下列说法中,不正确的个数是( )
①直径是弦;②经过圆内一定点可以作无数条直径;③平分弦的直径垂直于弦;④过三点可以作一个圆;⑤过圆心且垂直于切线的直线必过切点.
A.1个
B.2个
C.3个
D.4个
5.如图,⊙O的半径为4,A、B、C、D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A.4
B.2
C.4
D.值不确定
6.如图,PA,PB分别与⊙O相切于点A,B,连接OP,则下列判断错误的是( )
A.∠PAO=∠PBO=90°
B.OP平分∠APB
C.PA=PB
D.∠AOB=
7.已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:
①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG.则其中正确的是( )
A.①②④
B.③④
C.①②③
D.①②③④
8.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
9.正方形ABCD中,对角线AC、BD交于O,Q为CD上任意一点,AQ交BD于M,过M作MN⊥AM交BC于N,连AN、QN.下列结论:
①MA=MN;②∠AQD=∠AQN;③S△AQN=S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.
其中正确的结论有( )
A.①②③④
B.只有①③④
C.只有②③④
D.只有①②
10.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5
B.2
C.5或2
D.2或﹣1
二.填空题(共5小题)
11.如图,⊙O的半径为7cm,直线l⊥OA,垂足为B,OB=4cm,则直线l沿直线OA平移
cm时与⊙O相切.
12.已知⊙O的面积为9πcm2,若点O到直线L的距离为πcm,则直线l与⊙O的位置关系是
.
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为
.
14.如图,P是抛物线y=x2﹣4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为
.
15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为
.
三.解答题(共5小题)
16.如图所示,AB是圆O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和圆O的位置关系,并给出证明;
(2)当CE=5,BC=8时,求圆O的半径.
17.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.
求证:∠ACB为定值.
18.如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为的中点,连结CE交AB于点F,且BF=BC.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,sinB=,求CE的长.
19.如图,在Rt△ABC中,∠C=90°,在AC上取一点D,以AD为直径作⊙O,与AB相交于点E,作线段BE的垂直平分线MN交BC于点N,连接EN.
(1)求证:EN是⊙O的切线;
(2)若AC=3,BC=4,⊙O的半径为1.求线段EN与线段AE的长.
20.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
试题解析
一.选择题(共10小题)
1.圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离
B.相切
C.相交或相切
D.相离或相切
解:∵圆的半径为5cm,圆心与直线上某一点的距离为5cm,
∴直线与圆有交点
∴当圆心与该点的连线垂直于该直线时,由切线的判定定理可知,直线与圆相切;
当圆心与该点的连线不垂直于该直线时,则由垂线段最短,
可知圆心到该直线的距离小于5,从而直线与圆相交.
故选:C.
2.如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
A.0<CE≤8
B.0<CE≤5
C.3<CE≤8
D.3<CE≤5
解:如图,过A作AM⊥BC于N,CN⊥AD于N,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=5,
∴AM=CN,
∵AB=5,cosB=,
∴BM=4,
∵BC=8,
∴CM=4=BC,
∵AM⊥BC,
∴AC=AB=5,
由勾股定理得:AM=CN==3,
∴当以CE为半径的圆C与边AD有两个交点时,半径CE的取值范围是3<CE≤5,
故选:D.
3.⊙O的半径是3cm,圆心到直线的距离是4cm,则直线与⊙O的位置关系( )
A.相离
B.相切
C.相交
D.以上都不是
解:∵⊙O的半径是3cm,圆心到直线的距离是4cm,
∴4>3,
∴直线与⊙O的位置关系是相离,
故选:A.
4.下列说法中,不正确的个数是( )
①直径是弦;②经过圆内一定点可以作无数条直径;③平分弦的直径垂直于弦;④过三点可以作一个圆;⑤过圆心且垂直于切线的直线必过切点.
A.1个
B.2个
C.3个
D.4个
解:①直径是特殊的弦.所以①正确,不符合题意;
②经过圆心可以作无数条直径.所以②不正确,符合题意;
③平分弦(不是直径)的直径垂直于弦.所以③不正确,符合题意;
④过不在同一条直线上的三点可以作一个圆.所以④不正确,符合题意;
⑤过圆心且垂直于切线的直线必过切点.所以⑤正确,不符合题意.
故选:C.
5.如图,⊙O的半径为4,A、B、C、D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A.4
B.2
C.4
D.值不确定
解:当∠ADG=∠BCH=30°时,PE+PF是定值.
理由:连接OA、OB、OC、OD,如图:
∵DG与⊙O相切,
∴∠GDA=∠ABD.
∵∠ADG=30°,
∴∠ABD=30°.
∴∠AOD=2∠ABD=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA.
∴=,=.
∴+=+=1.
∴+=1.
∴PE+PF=4.
∴当∠ADG=∠BCH=30°时,PE+PF=4.
故选:A.
6.如图,PA,PB分别与⊙O相切于点A,B,连接OP,则下列判断错误的是( )
A.∠PAO=∠PBO=90°
B.OP平分∠APB
C.PA=PB
D.∠AOB=
解:∵PA,PB分别与⊙O相切于点A,B,
∴∠PAO=∠PBO=90°,OP平分∠APB,PA=PB,
则A、B、C正确,不符合题意;
∠AOB的度数与的度数相等,D错误,符合题意;
故选:D.
7.已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:
①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG.则其中正确的是( )
A.①②④
B.③④
C.①②③
D.①②③④
解:连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,
∵OD=OB,
∴∠ABD=∠ODB,
∵∠AOD=∠OBD+∠ODB=2∠OBD,
∵∠AOD=2∠ABC,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
∵AB是直径,
∴CD⊥AB,
∴①正确;
∵CD⊥AB,
∴∠P+∠PCD=90°,
∵OD=OC,
∴∠OCD=∠ODC=∠P,
∴∠PCD+∠OCD=90°,
∴∠PCO=90°,
∴PC是切线,∴②正确;
假设OD∥GF,则∠AOD=∠FEB=2∠ABC,
∴3∠ABC=90°,
∴∠ABC=30°,
已知没有给出∠B=30°,∴③错误;
∵AB是直径,
∴∠ACB=90°,
∵EF⊥BC,
∴AC∥EF,
∴弧CF=弧AG,
∴AG=CF,
∵OQ⊥CF,OZ⊥BG,
∴CQ=AG,OZ=AG,BZ=BG,
∴OZ=CQ,
∵OC=OB,∠OQC=∠OZB=90°,
∴△OCQ≌△BOZ,
∴OQ=BZ=BG,
∴④正确.
故选:A.
8.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选:A.
9.正方形ABCD中,对角线AC、BD交于O,Q为CD上任意一点,AQ交BD于M,过M作MN⊥AM交BC于N,连AN、QN.下列结论:
①MA=MN;②∠AQD=∠AQN;③S△AQN=S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.
其中正确的结论有( )
A.①②③④
B.只有①③④
C.只有②③④
D.只有①②
解:
延长CD到F,使DF=BN,连接AF,过A作AH⊥NQ于H,
∵正方形ABCD,NM⊥AQ,
∴∠AMN=∠ABC=90°,
∴ABNM四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴MA=MN,∴①正确;
∵正方形ABCD,
∴∠ABN=∠ADF=90°,AD=AB,
在△ABN和△ADF中
∵,
∴△ABN≌△ADF,
∴∠FAD=∠BAN,AF=AN,
∵∠NAM=∠BAC=45°,
∴∠FAQ=∠FAD+∠DAQ=45°=∠NAQ,
在△NAQ和△FAQ中
∵,
∴△NAQ≌△FAQ,
∴∠AQN=∠AQD,∴②正确;
在△ADQ和△AHQ中
∵,
∴△ADQ≌△AHQ,
∴S△ADQ=S△AQH,
∴S△NAQ=S△FAQ=S△FAD+S△ADQ=S五边形ABNQD,
∴③正确;
∵AH=AD=AB,AH⊥NQ,
∴QN是以A为圆心,以AB为半径的圆的切线,
∴④正确.
故选:A.
10.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5
B.2
C.5或2
D.2或﹣1
解:设直角三角形ABC内切圆的圆心为点I,半径为r,
三边上的切点分别为D、E、F,
连接ID、IE、IF,
得正方形,则正方形的边长即为r,
如图所示:
当BC为直角边时,
AC==10,
根据切线长定理,得
AD=AF=AB﹣BD=6﹣r,
CE=CF=BC﹣BE=8﹣r,
∴AF+FC=AC=10,
即6﹣r+8﹣r=10,解得r=2;
当BC为斜边时,
AC==2,
根据切线长定理,得
BD=BF=6﹣r,
CE=CF=2﹣r,
∴BC=BF+CF=6﹣r+2﹣r=8,
解得r=﹣1.
答:这个三角形的内切圆的半径是2或﹣1.
故选:D.
二.填空题(共5小题)
11.如图,⊙O的半径为7cm,直线l⊥OA,垂足为B,OB=4cm,则直线l沿直线OA平移 3或11 cm时与⊙O相切.
解:
延长AO交圆O于C,
当直线l平移到过A点或过C点时,直线l与圆相切,
AB=OA﹣OB=7﹣4=3,BC=OC+0B=7+4=11,
故答案为:3或11.
12.已知⊙O的面积为9πcm2,若点O到直线L的距离为πcm,则直线l与⊙O的位置关系是 相离 .
解:设⊙O的半径是rcm,
∵⊙O的面积为9πcm2,
∴πr2=9π,
∴r=3(cm),
∵点O到直线L的距离d为πcm,
∴d>r.
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为 6 .
解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO﹣∠PAB=90°﹣60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=2,
∴△PAB的周长=6.
故答案为:6.
14.如图,P是抛物线y=x2﹣4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为 (2+,1)或(2﹣,1)或(2,﹣1) .
解:当y=1时,x2﹣4x+3=1,
解得:x=2±,
∴P(2+,1)或(2﹣,1),
当y=﹣1时,x2﹣4x+3=﹣1,
解得:x1=x2=2,
∴P(2,﹣1),
则点P的坐标为:(2+,1)或(2﹣,1)或(2,﹣1).
15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 44 .
解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故答案为:44.
三.解答题(共5小题)
16.如图所示,AB是圆O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和圆O的位置关系,并给出证明;
(2)当CE=5,BC=8时,求圆O的半径.
解:(1)直线BD和⊙O相切.
证明:∵∠AEC=∠ODB,∠AEC=∠ABC,
∴∠ABC=∠ODB,
∵OD⊥BC,
∴∠DBC+∠ODB=90°,
∴∠DBC+∠ABC=90°,
∴∠DBO=90°,
∴直线BD和⊙O相切;
(2)∵OD⊥BC,BC=8,
∴BF=CF=4,
在Rt△CEF中,EF==3,
设圆O的半径为r,则OF=r﹣3,
在Rt△OBF中,OB2=OF2+BF2,即r2=(r﹣3)2+42,
解得,r=,即圆O的半径为.
17.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.
求证:∠ACB为定值.
证明:连接AM,BM,
由题意得:M是内心,
∴AM平分∠CAB,BM平分∠ABC,
∴∠CAM=∠BAM,∠CBM=∠ABM,
∴∠AMB=180°﹣∠BAM﹣∠ABM,
∴∠BAM+∠ABM=180°﹣∠AMB,
△ABC中,∠C=180°﹣(∠CAB+∠ACB)=180°﹣2∠BAM﹣2∠ABM=180°﹣2(180°﹣∠AMB)=2∠AMB﹣180°,
∵所在圆是个定圆,弦AB和半径都是定值,
∴∠AMB为定值,
∴∠ACB为定值2∠AMB﹣180°.
18.如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为的中点,连结CE交AB于点F,且BF=BC.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,sinB=,求CE的长.
(1)BC与⊙O相切
证明:连接AE,
∵AC是⊙O的直径
∴∠E=90°,
∴∠EAD+∠AFE=90°,
∵BF=BC,
∴∠BCE=∠BFC,
∵E为弧AD中点,
∴∠EAD=∠ACE,
∴∠BCE+∠ACE=90°,
∴AC⊥BC,
∵AC为直径,
∴BC是⊙O的切线.
(2)解:∵⊙O的半为2
∴AC=4,
∵sinB==,
∴AB=5,
∴BC==3,
∵BF=BC,
∴BF=3,AF=5﹣3=2,
∵∠EAD=∠ACE,∠E=∠E,
∴△AEF∽△CEA,
∴==,
∴EC=2EA,
设EA=x,EC=2x,
由勾股定理得:x2+4x2=16,
x=(负数舍去),
即CE=.
19.如图,在Rt△ABC中,∠C=90°,在AC上取一点D,以AD为直径作⊙O,与AB相交于点E,作线段BE的垂直平分线MN交BC于点N,连接EN.
(1)求证:EN是⊙O的切线;
(2)若AC=3,BC=4,⊙O的半径为1.求线段EN与线段AE的长.
解:(1)证明:如图,连接OE,
∵NM是BE的垂直平分线,
BN=EN,
∴∠B=∠NEB,
∵OA=OE
∴∠A=∠OEA,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠OEN=90°,即OE⊥EN,
∵OE是半径,
∴EN是⊙O的切线;
(2)如图,连接ON,
设EN长为x,则BN=EN=x
∵AC=3,BC=4,⊙O的半径为1,
∴CN=4﹣x,OC=AC﹣OA=3﹣1=2,
∴OE2+EN2=OC2+CN2,
∴12+x2=22+(4﹣x)2,
解得x=,
∴EN=.
连接ED,DB,设AE=y,
∵AC=3,BC=4,
∴AB=5,
∵⊙O的半径为1.
∴AD=2,
则DE2=AD2﹣AE2=22﹣y2,
∵CD=AC﹣AD=3﹣2=1,
∴DB2=CD2+BC2=17,
∵AD为直径,
∴∠AED=∠DEB=90,
∴DE2+EB2=DB2,
即22﹣y2+(5﹣y)2=17,
解得y=,
∴EN=,AE=.
20.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
解:(1)∵PA,PB是⊙O的切线,
∴AP=BP,
∵∠P=60°,
∴∠PAB=60°,
∵AC是⊙O的直径,
∴∠PAC=90°,
∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
