24.3 正多边形和圆 高频易错题集 (原卷+解析)
文档属性
| 名称 | 24.3 正多边形和圆 高频易错题集 (原卷+解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 800.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.3
正多边形和圆
高频易错题集
一.选择题(共10小题)
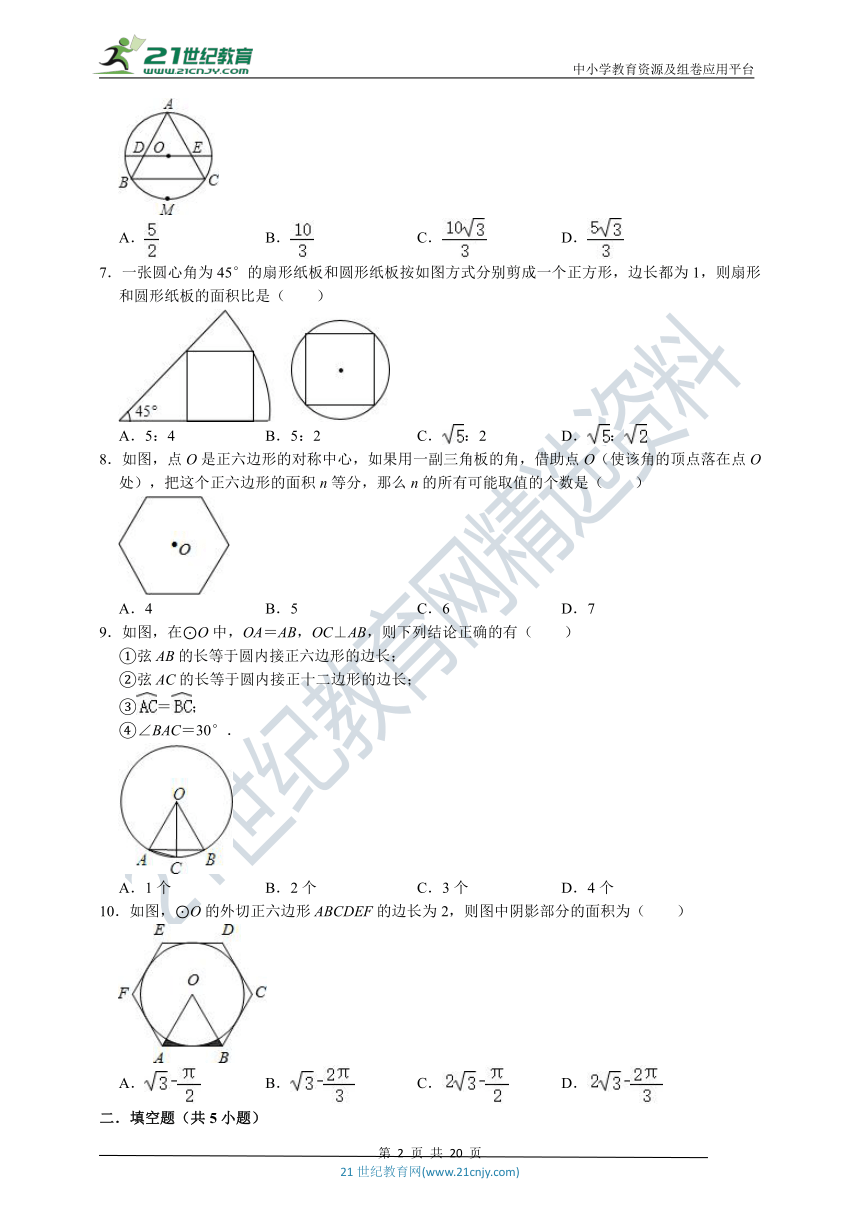
1.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2
B.
C.3
D.
2.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度(米)为( )
A.2
B.4
C.4
D.4π
3.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2
B.a2﹣b2
C.a+b
D.ab
4.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是( )
A.
B.
C.
D.2
5.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.
B.
C.
D.
6.如图,把正△ABC的外接圆对折,使点A与劣弧BC的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )
A.
B.
C.
D.
7.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4
B.5:2
C.:2
D.:
8.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
A.4
B.5
C.6
D.7
9.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有( )
①弦AB的长等于圆内接正六边形的边长;
②弦AC的长等于圆内接正十二边形的边长;
③=;
④∠BAC=30°.
A.1个
B.2个
C.3个
D.4个
10.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
A.
B.
C.
D.
二.填空题(共5小题)
11.如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是
.
12.点A、C为半径是6的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为
.
13.如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而=45°是360°(多边形外角和)的,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
图2中的图案外轮廓周长是
;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是
.
14.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=
.
15.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是
度.
三.解答题(共5小题)
16.(1)已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN,证明△ABM≌△BCN,并求出∠BQM的度数.
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、正六边形ABCDEF、正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形
正方形
正五边形
正六边形
…
正n边形
∠BQM的度数
…
17.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
18.已知圆内接正n边形A1,A2,A3…An﹣1,An,p是圆上异于An﹣2,An的弧An﹣2A1An上的一点,求的值.
19.在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
20.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:AB?r1+AC?r2=AB?h,∴r1+r2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,试证明:.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于
;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…rn,请问r1+r2+…rn是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.
试题解析
一.选择题(共10小题)
1.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2
B.
C.3
D.
解:设DE与⊙O相切于点N,连接OD、OE、ON,作DM⊥OE于M,如图所示:
则ON⊥DE,DE=2,OD=OE,∠DOE==45°,
∵DM⊥OE,
∴△ODM是等腰直角三角形,
∴DM=OM,OE=OD=DM,
设OM=DM=x,则OD=OE=x,EM=OE﹣OM=(﹣1)x,
在Rt△DEM中,由勾股定理得:x2+(﹣1)2x2=22,
解得:x2=2+,
∵△ODE的面积=DE×ON=OE×DM,
∴ON====+1,
即⊙O的半径为:1+;
故选:B.
2.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度(米)为( )
A.2
B.4
C.4
D.4π
解:正方形桌布对角线长度为圆形桌面的直径加上两个高,即2+1+1=4(米),
设正方形边长是x米,则
x2+x2=42,
解得:x=2,
所以正方形桌布的边长是2米.
故选:A.
3.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2
B.a2﹣b2
C.a+b
D.ab
解:如图所示,在正八边形中,最长的对角线为AE=BF=CG=DH=a,
最短得对角线为AC=BD=CE=DF=EG=FH=GA=HB=b,
按图所示进行割补得,
S正八边形ABCDEFGH=S四边形PQMN=ab.
故选:D.
4.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是( )
A.
B.
C.
D.2
解:如图,连接AC、BD、OF,,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=r?sin60°=,
∴EF=,
∵AO=2OI,
∴OI=,CI=r﹣=,
∴,
∴,
∴=,
即则的值是.
故选:C.
5.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.
B.
C.
D.
解:连接OE1,OD1,OD2,如图,
∵六边形A1B1C1D1E1F1为正六边形,
∴∠E1OD1=60°,
∴△E1OD1为等边三角形,
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,
∴OD2⊥E1D1,
∴OD2=E1D1=×2,
∴正六边形A2B2C2D2E2F2的边长=×2,
同理可得正六边形A3B3C3D3E3F3的边长=()2×2,
则正六边形A10B10C10D10E10F10的边长=()9×2=.
故选:D.
6.如图,把正△ABC的外接圆对折,使点A与劣弧BC的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )
A.
B.
C.
D.
解:连接AM、OB,则其交点O即为此圆的圆心;
∵△ABC是正三角形,
∴∠OBC=∠OAD=30°,DE∥BC,
在Rt△OBF中,BF=BC=×5=,
∴OB===,
∴OA=OB=;
在Rt△AOD中,∠DAO=30°,
∴OD=OA?tan30°=×=,
∴DE=2OD=2×=.
故选:B.
7.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4
B.5:2
C.:2
D.:
解:如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=1,
∵∠AOB=45°,
∴OB=AB=1,
由勾股定理得:OD==,
∴扇形的面积是=π;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=1,
∴MC=MB=,
∴⊙M的面积是π×()2=π,
∴扇形和圆形纸板的面积比是π÷(π)=.
故选:A.
8.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
A.4
B.5
C.6
D.7
解:360°÷30°=12;
360°÷60°=6;
360°÷90°=4;
360°÷120°=3;
360°÷180°=2;
因此n的所有可能的值共5种情况,
故选:B.
9.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有( )
①弦AB的长等于圆内接正六边形的边长;
②弦AC的长等于圆内接正十二边形的边长;
③=;
④∠BAC=30°.
A.1个
B.2个
C.3个
D.4个
解:∵OA=AB,OA=OB,
∴△OAB是等边三角形,
∴∠AOB=∠OAB=∠OBA=60°,
∴弦AB的长等于圆内接正六边形的边长,故①正确;
∵OC⊥AB,
∴AC=BC,
∴=,故③正确;
∴弦AC的长等于圆内接正十二边形的边长,故②正确;
∵∠ACB是圆内接正十二边形的内角,
∴∠ACB==150°,
∴∠ACO=∠ACB=×150°=75°,
在△AOC中,
∵∠AOC=30°,∠OAB=60°,∠ACO=75°,
∴∠BAC=180°﹣∠ACO﹣∠AOC﹣∠OAC=180°﹣75°﹣30°﹣60°=15°,故④错误.
故选:C.
10.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
A.
B.
C.
D.
解:∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=2,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA?sin60°=2×=,
∴S阴影=S△OAB﹣S扇形OMN=×2×﹣=﹣.
故选:A.
二.填空题(共5小题)
11.如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是 (20+20)cm .
解:如图所示:可得MN=BC=20cm,
△OWM是等边三角形,边长为10cm,
则它的高为:=5(cm),
故FG=20+4×5=(20+20)cm.
故答案为:(20+20)cm.
12.点A、C为半径是6的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 2或4 .
解:分两种情况:
①如图,OB=OC=6,
∵点B为的中点,
∴AB=BC,
∵顶点D恰在该圆直径的三等分点上,
∴BD=2×6÷3=4,
∴DE=BE=2,
∴OE=OB﹣BE=6﹣2=4,
在Rt△DEC中,根据勾股定理,得
CE===2,
在Rt△DEC中,根据勾股定理,得
∴CD==2;
②如图,
同理可得,BD=12﹣2×6÷3=12﹣4=8,
∴DE=BE=4,
∴OE=OB﹣BE=6﹣4=2,
在Rt△OEC中,根据勾股定理,得
CE===4,
在Rt△DEC中,根据勾股定理,得
∴CD==4.
综上所述:该菱形的边长为2或4.
故答案为:2或4.
13.如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而=45°是360°(多边形外角和)的,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
图2中的图案外轮廓周长是 14 ;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是 21 .
解:图2中的图案外轮廓周长是:8+8﹣2=14;
设∠BPC=2x,
∴以∠BPC为内角的正多边形的边数为:=,
以∠APB为内角的正多边形的边数为:,
∴图案外轮廓周长是=﹣2+﹣2+﹣2=+﹣6,
根据题意可知:2x的值只能为60°,90°,120°,144°,
∴当x=30时,周长最大,此时图案定为会标,
则会标的外轮廓周长是=+﹣6=21,
故答案为:14,21.
14.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM= 48° .
解:连接OA,
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠BOM=∠AOM﹣∠AOB=48°,
故答案为:48°.
15.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是 72 度.
解:连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为:72.
三.解答题(共5小题)
16.(1)已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN,证明△ABM≌△BCN,并求出∠BQM的度数.
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、正六边形ABCDEF、正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形
正方形
正五边形
正六边形
…
正n边形
∠BQM的度数
90°
108°
120°
…
(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠C=60°,
在△ABM和△BCN中,
,
∴△ABM≌△BCN,
∴∠BAM=∠CBN,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=60°;
(2)正方形ABCD中,由(1)得,△ABM≌△BCN,
∴∠BAM=∠CBN,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=90°,
同理正五边形ABCDE中,∠BQM=108°,
正六边形ABCDEF中,∠BQM=120°,
正n边形ABCD…中,∠BQM=,
故答案为:90°;108°;120°;.
17.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
(1)证明:∵六边形ABCDEF为正六边形,
∴每个内角均为120°.
∵∠FMH=120°,A、M、B在一条直线上,
∴∠AFM+∠FMA=∠FMA+∠BMH=60°,
∴∠AFM=∠BMH.
(2)解:猜想:FM=MH.
证明:①当点M与点A重合时,∠FMB=120°,MB与BQ的交点H与点B重合,有FM=MH.
②当点M与点A不重合时,
证法一:如图1,连接FB并延长到G,使BG=BH,连接MG.
∵∠BAF=120°,AF=AB,
∴∠ABF=30°,
∴∠ABG=180°﹣30°=150°.
∵MH与六边形外角的平分线BQ交于点H,
∴∠CBQ=×60°=30°,
∴∠MBH=∠ABC+∠CBQ=120°+30°=150°,
∴∠MBH=∠MBG=150°.
∵,
∴△MBH≌△MBG,
∴∠MHB=∠MGB,MH=MG,
∵∠AFM=∠BMH,∠HMB+∠MHB=30°,
∴∠AFM+∠MGB=30°,
∵∠AFM+∠MFB=30°,
∴∠MFB=∠MGB.
∴FM=MG=MH.
证法二:如图2,在AF上截取FP=MB,连接PM.
∵AF=AB,FP=MB,
∴PA=AM
∵∠A=120°,
∴∠APM=×(180°﹣120°)=30°,
有∠FPM=150°,
∵BQ平分∠CBN,
∴∠MBQ=120°+30°=150°,
∴∠FPM=∠MBH,
由(1)知∠PFM=∠HMB,
∴△FPM≌△MBH.
∴FM=MH.
18.已知圆内接正n边形A1,A2,A3…An﹣1,An,p是圆上异于An﹣2,An的弧An﹣2A1An上的一点,求的值.
解:如图,连接An﹣2An,过An﹣2作An﹣1M⊥An于M,
∵=,且它们的度数均为,
∴∠An﹣2AnAn﹣1=,
设An﹣2AnAn﹣1=An﹣2AnAn=a,
∴AnM=acos,
∴An﹣2An=2acos,
∵PAn﹣2An﹣1An为圆内接四边形,由托勒密定理(圆内接四边形两组对边乘积的和等于两条对角线的乘积)得:
PAn﹣2An﹣1An+PAnAn﹣2An﹣1=PAn﹣1An﹣2An,即a(PAn﹣2+PAn)=PAn﹣1?2cos,
∴=2cos.
故答案为:2cos.
19.在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为 5 cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为 10 cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为 10 cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
解:(1)(Ⅰ)连接BD,
∵AD=3×5=15cm,AB=5cm,
∴BD==cm;
(Ⅱ)如图所示,
∵三个正方形的边长均为5,
∴A、B、C三点在以O为圆心,以OA为半径的圆上,
∴OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为10cm;
(Ⅲ)如图所示,
∵CE⊥AB,AC=BC,
∴AD是过A、B、C三点的圆的直径,
∵OA=OB=OD,
∴O为圆心,
∴⊙O的半径为OA,
OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为5×2=10cm;
(2)如图④为盖住三个正方形时直径最小的放置方法,
连接OB,ON,延长OH交AB于点P,则OP⊥AB,P为AB中点,
设OG=x,则OP=10﹣x,
则有:,
解得:,(8分)
则ON=,
∴直径为.
20.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:AB?r1+AC?r2=AB?h,∴r1+r2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,试证明:.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于 4 ;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…rn,请问r1+r2+…rn是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.
解:(1)分别连接AP,BP,CP,作AD⊥BC于D,
∴∠ADB=90°,
∵△ABC是等边三角形
∴AB=BC=AC=2,∠ABC=60°,
∴∠BAD=30°,
∴BD=1,在Rt△ABD中,由勾股定理,得
∴AD=
∵S△ABP+S△BCP+S△ACP=S△ABC.
∴AB?r1+BC?r2+AC?r3=BC×AD,
∵BC=AC=AB,
∴r1+r2+r3=AD.
∴r1+r2+r3=
(2)如图2,∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD=2.
∵PE⊥AB,PF⊥BC,PG⊥DC,PH⊥AD,
∴四边形PEBF是矩形,四边形PFCG是矩形,四边形PGDH是矩形,四边形PHAE是矩形,
∴PE=AH,PF=BE,PG=HD,PH=AE,
∴PE+PF+PG+PH=AH+BE+HD+AE=AD+AB=4.
故答案为4.
(3)设正n边形的边心距为r,且正n边形的边长为2,
∴S正n边形=×2×r×n.r=,
∵S正n边形=×2×r1+×2×r2+×2×r1+…+×2×rn,
∴×2×r1+×2×r2+×2×r1+…+×2×rn=×n,
∴r1+r2+…+rn=nr=(为定值).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
24.3
正多边形和圆
高频易错题集
一.选择题(共10小题)
1.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2
B.
C.3
D.
2.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度(米)为( )
A.2
B.4
C.4
D.4π
3.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2
B.a2﹣b2
C.a+b
D.ab
4.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是( )
A.
B.
C.
D.2
5.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.
B.
C.
D.
6.如图,把正△ABC的外接圆对折,使点A与劣弧BC的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )
A.
B.
C.
D.
7.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4
B.5:2
C.:2
D.:
8.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
A.4
B.5
C.6
D.7
9.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有( )
①弦AB的长等于圆内接正六边形的边长;
②弦AC的长等于圆内接正十二边形的边长;
③=;
④∠BAC=30°.
A.1个
B.2个
C.3个
D.4个
10.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
A.
B.
C.
D.
二.填空题(共5小题)
11.如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是
.
12.点A、C为半径是6的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为
.
13.如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而=45°是360°(多边形外角和)的,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
图2中的图案外轮廓周长是
;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是
.
14.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=
.
15.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是
度.
三.解答题(共5小题)
16.(1)已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN,证明△ABM≌△BCN,并求出∠BQM的度数.
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、正六边形ABCDEF、正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形
正方形
正五边形
正六边形
…
正n边形
∠BQM的度数
…
17.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
18.已知圆内接正n边形A1,A2,A3…An﹣1,An,p是圆上异于An﹣2,An的弧An﹣2A1An上的一点,求的值.
19.在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
20.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:AB?r1+AC?r2=AB?h,∴r1+r2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,试证明:.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于
;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…rn,请问r1+r2+…rn是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.
试题解析
一.选择题(共10小题)
1.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2
B.
C.3
D.
解:设DE与⊙O相切于点N,连接OD、OE、ON,作DM⊥OE于M,如图所示:
则ON⊥DE,DE=2,OD=OE,∠DOE==45°,
∵DM⊥OE,
∴△ODM是等腰直角三角形,
∴DM=OM,OE=OD=DM,
设OM=DM=x,则OD=OE=x,EM=OE﹣OM=(﹣1)x,
在Rt△DEM中,由勾股定理得:x2+(﹣1)2x2=22,
解得:x2=2+,
∵△ODE的面积=DE×ON=OE×DM,
∴ON====+1,
即⊙O的半径为:1+;
故选:B.
2.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度(米)为( )
A.2
B.4
C.4
D.4π
解:正方形桌布对角线长度为圆形桌面的直径加上两个高,即2+1+1=4(米),
设正方形边长是x米,则
x2+x2=42,
解得:x=2,
所以正方形桌布的边长是2米.
故选:A.
3.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2
B.a2﹣b2
C.a+b
D.ab
解:如图所示,在正八边形中,最长的对角线为AE=BF=CG=DH=a,
最短得对角线为AC=BD=CE=DF=EG=FH=GA=HB=b,
按图所示进行割补得,
S正八边形ABCDEFGH=S四边形PQMN=ab.
故选:D.
4.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是( )
A.
B.
C.
D.2
解:如图,连接AC、BD、OF,,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=r?sin60°=,
∴EF=,
∵AO=2OI,
∴OI=,CI=r﹣=,
∴,
∴,
∴=,
即则的值是.
故选:C.
5.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.
B.
C.
D.
解:连接OE1,OD1,OD2,如图,
∵六边形A1B1C1D1E1F1为正六边形,
∴∠E1OD1=60°,
∴△E1OD1为等边三角形,
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,
∴OD2⊥E1D1,
∴OD2=E1D1=×2,
∴正六边形A2B2C2D2E2F2的边长=×2,
同理可得正六边形A3B3C3D3E3F3的边长=()2×2,
则正六边形A10B10C10D10E10F10的边长=()9×2=.
故选:D.
6.如图,把正△ABC的外接圆对折,使点A与劣弧BC的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )
A.
B.
C.
D.
解:连接AM、OB,则其交点O即为此圆的圆心;
∵△ABC是正三角形,
∴∠OBC=∠OAD=30°,DE∥BC,
在Rt△OBF中,BF=BC=×5=,
∴OB===,
∴OA=OB=;
在Rt△AOD中,∠DAO=30°,
∴OD=OA?tan30°=×=,
∴DE=2OD=2×=.
故选:B.
7.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4
B.5:2
C.:2
D.:
解:如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=1,
∵∠AOB=45°,
∴OB=AB=1,
由勾股定理得:OD==,
∴扇形的面积是=π;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=1,
∴MC=MB=,
∴⊙M的面积是π×()2=π,
∴扇形和圆形纸板的面积比是π÷(π)=.
故选:A.
8.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
A.4
B.5
C.6
D.7
解:360°÷30°=12;
360°÷60°=6;
360°÷90°=4;
360°÷120°=3;
360°÷180°=2;
因此n的所有可能的值共5种情况,
故选:B.
9.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有( )
①弦AB的长等于圆内接正六边形的边长;
②弦AC的长等于圆内接正十二边形的边长;
③=;
④∠BAC=30°.
A.1个
B.2个
C.3个
D.4个
解:∵OA=AB,OA=OB,
∴△OAB是等边三角形,
∴∠AOB=∠OAB=∠OBA=60°,
∴弦AB的长等于圆内接正六边形的边长,故①正确;
∵OC⊥AB,
∴AC=BC,
∴=,故③正确;
∴弦AC的长等于圆内接正十二边形的边长,故②正确;
∵∠ACB是圆内接正十二边形的内角,
∴∠ACB==150°,
∴∠ACO=∠ACB=×150°=75°,
在△AOC中,
∵∠AOC=30°,∠OAB=60°,∠ACO=75°,
∴∠BAC=180°﹣∠ACO﹣∠AOC﹣∠OAC=180°﹣75°﹣30°﹣60°=15°,故④错误.
故选:C.
10.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
A.
B.
C.
D.
解:∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=2,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA?sin60°=2×=,
∴S阴影=S△OAB﹣S扇形OMN=×2×﹣=﹣.
故选:A.
二.填空题(共5小题)
11.如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是 (20+20)cm .
解:如图所示:可得MN=BC=20cm,
△OWM是等边三角形,边长为10cm,
则它的高为:=5(cm),
故FG=20+4×5=(20+20)cm.
故答案为:(20+20)cm.
12.点A、C为半径是6的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 2或4 .
解:分两种情况:
①如图,OB=OC=6,
∵点B为的中点,
∴AB=BC,
∵顶点D恰在该圆直径的三等分点上,
∴BD=2×6÷3=4,
∴DE=BE=2,
∴OE=OB﹣BE=6﹣2=4,
在Rt△DEC中,根据勾股定理,得
CE===2,
在Rt△DEC中,根据勾股定理,得
∴CD==2;
②如图,
同理可得,BD=12﹣2×6÷3=12﹣4=8,
∴DE=BE=4,
∴OE=OB﹣BE=6﹣4=2,
在Rt△OEC中,根据勾股定理,得
CE===4,
在Rt△DEC中,根据勾股定理,得
∴CD==4.
综上所述:该菱形的边长为2或4.
故答案为:2或4.
13.如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而=45°是360°(多边形外角和)的,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
图2中的图案外轮廓周长是 14 ;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是 21 .
解:图2中的图案外轮廓周长是:8+8﹣2=14;
设∠BPC=2x,
∴以∠BPC为内角的正多边形的边数为:=,
以∠APB为内角的正多边形的边数为:,
∴图案外轮廓周长是=﹣2+﹣2+﹣2=+﹣6,
根据题意可知:2x的值只能为60°,90°,120°,144°,
∴当x=30时,周长最大,此时图案定为会标,
则会标的外轮廓周长是=+﹣6=21,
故答案为:14,21.
14.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM= 48° .
解:连接OA,
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠BOM=∠AOM﹣∠AOB=48°,
故答案为:48°.
15.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是 72 度.
解:连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为:72.
三.解答题(共5小题)
16.(1)已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN,证明△ABM≌△BCN,并求出∠BQM的度数.
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、正六边形ABCDEF、正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形
正方形
正五边形
正六边形
…
正n边形
∠BQM的度数
90°
108°
120°
…
(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠C=60°,
在△ABM和△BCN中,
,
∴△ABM≌△BCN,
∴∠BAM=∠CBN,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=60°;
(2)正方形ABCD中,由(1)得,△ABM≌△BCN,
∴∠BAM=∠CBN,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=90°,
同理正五边形ABCDE中,∠BQM=108°,
正六边形ABCDEF中,∠BQM=120°,
正n边形ABCD…中,∠BQM=,
故答案为:90°;108°;120°;.
17.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
(1)证明:∵六边形ABCDEF为正六边形,
∴每个内角均为120°.
∵∠FMH=120°,A、M、B在一条直线上,
∴∠AFM+∠FMA=∠FMA+∠BMH=60°,
∴∠AFM=∠BMH.
(2)解:猜想:FM=MH.
证明:①当点M与点A重合时,∠FMB=120°,MB与BQ的交点H与点B重合,有FM=MH.
②当点M与点A不重合时,
证法一:如图1,连接FB并延长到G,使BG=BH,连接MG.
∵∠BAF=120°,AF=AB,
∴∠ABF=30°,
∴∠ABG=180°﹣30°=150°.
∵MH与六边形外角的平分线BQ交于点H,
∴∠CBQ=×60°=30°,
∴∠MBH=∠ABC+∠CBQ=120°+30°=150°,
∴∠MBH=∠MBG=150°.
∵,
∴△MBH≌△MBG,
∴∠MHB=∠MGB,MH=MG,
∵∠AFM=∠BMH,∠HMB+∠MHB=30°,
∴∠AFM+∠MGB=30°,
∵∠AFM+∠MFB=30°,
∴∠MFB=∠MGB.
∴FM=MG=MH.
证法二:如图2,在AF上截取FP=MB,连接PM.
∵AF=AB,FP=MB,
∴PA=AM
∵∠A=120°,
∴∠APM=×(180°﹣120°)=30°,
有∠FPM=150°,
∵BQ平分∠CBN,
∴∠MBQ=120°+30°=150°,
∴∠FPM=∠MBH,
由(1)知∠PFM=∠HMB,
∴△FPM≌△MBH.
∴FM=MH.
18.已知圆内接正n边形A1,A2,A3…An﹣1,An,p是圆上异于An﹣2,An的弧An﹣2A1An上的一点,求的值.
解:如图,连接An﹣2An,过An﹣2作An﹣1M⊥An于M,
∵=,且它们的度数均为,
∴∠An﹣2AnAn﹣1=,
设An﹣2AnAn﹣1=An﹣2AnAn=a,
∴AnM=acos,
∴An﹣2An=2acos,
∵PAn﹣2An﹣1An为圆内接四边形,由托勒密定理(圆内接四边形两组对边乘积的和等于两条对角线的乘积)得:
PAn﹣2An﹣1An+PAnAn﹣2An﹣1=PAn﹣1An﹣2An,即a(PAn﹣2+PAn)=PAn﹣1?2cos,
∴=2cos.
故答案为:2cos.
19.在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为 5 cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为 10 cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为 10 cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
解:(1)(Ⅰ)连接BD,
∵AD=3×5=15cm,AB=5cm,
∴BD==cm;
(Ⅱ)如图所示,
∵三个正方形的边长均为5,
∴A、B、C三点在以O为圆心,以OA为半径的圆上,
∴OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为10cm;
(Ⅲ)如图所示,
∵CE⊥AB,AC=BC,
∴AD是过A、B、C三点的圆的直径,
∵OA=OB=OD,
∴O为圆心,
∴⊙O的半径为OA,
OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为5×2=10cm;
(2)如图④为盖住三个正方形时直径最小的放置方法,
连接OB,ON,延长OH交AB于点P,则OP⊥AB,P为AB中点,
设OG=x,则OP=10﹣x,
则有:,
解得:,(8分)
则ON=,
∴直径为.
20.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:AB?r1+AC?r2=AB?h,∴r1+r2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,试证明:.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于 4 ;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…rn,请问r1+r2+…rn是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.
解:(1)分别连接AP,BP,CP,作AD⊥BC于D,
∴∠ADB=90°,
∵△ABC是等边三角形
∴AB=BC=AC=2,∠ABC=60°,
∴∠BAD=30°,
∴BD=1,在Rt△ABD中,由勾股定理,得
∴AD=
∵S△ABP+S△BCP+S△ACP=S△ABC.
∴AB?r1+BC?r2+AC?r3=BC×AD,
∵BC=AC=AB,
∴r1+r2+r3=AD.
∴r1+r2+r3=
(2)如图2,∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD=2.
∵PE⊥AB,PF⊥BC,PG⊥DC,PH⊥AD,
∴四边形PEBF是矩形,四边形PFCG是矩形,四边形PGDH是矩形,四边形PHAE是矩形,
∴PE=AH,PF=BE,PG=HD,PH=AE,
∴PE+PF+PG+PH=AH+BE+HD+AE=AD+AB=4.
故答案为4.
(3)设正n边形的边心距为r,且正n边形的边长为2,
∴S正n边形=×2×r×n.r=,
∵S正n边形=×2×r1+×2×r2+×2×r1+…+×2×rn,
∴×2×r1+×2×r2+×2×r1+…+×2×rn=×n,
∴r1+r2+…+rn=nr=(为定值).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
