2020-2021学年苏科新版八年级上册数学《第1章 全等三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科新版八年级上册数学《第1章 全等三角形》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 220.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 00:00:00 | ||
图片预览




文档简介
2020-2021学年苏科新版八年级上册数学《第1章
全等三角形》单元测试卷
一.选择题
1.下列各组中的两个图形为全等形的是( )
A.两块三角尺
B.两枚硬币
C.两张A4纸
D.两片枫树叶
2.平移前后两个图形是全等图形,对应点连线( )
A.平行但不相等
B.不平行也不相等
C.平行且相等
D.不相等
3.如图,△AEC≌△ADB,若∠A=50°,∠ABD=38°,则图中∠AEC的度数是( )
A.88°
B.92°
C.95°
D.102°
4.如图,△ABC≌△A′B′C,则图中所有角中与∠BCB′相等的角(除∠BCB′外)共有( )
A.1个
B.2个
C.3个
D.4个
5.一个三角形中,已知一个角为30°,两条边长为4和6,符合条件且互不全等的三角形有( )个.
A.1个
B.2个
C.3个
D.4个
6.如图,AC⊥BC,BD⊥AD,AC=BD,则判定△ABC与△BAD全等的依据是( )
A.HL
B.SAS
C.ASA
D.AAS
7.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS
B.AAS
C.ASA
D.SAS
8.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS
B.ASA
C.SAS
D.HL
9.在△ABC中,AB=5,AC=7,则中线AD的取值范围是( )
A.1<AD<7
B.1<AD<8
C.1<AD<6
D.2<AD<5
10.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.斜边和一直角边对应相等
D.斜边和一锐角对应相等
二.填空题
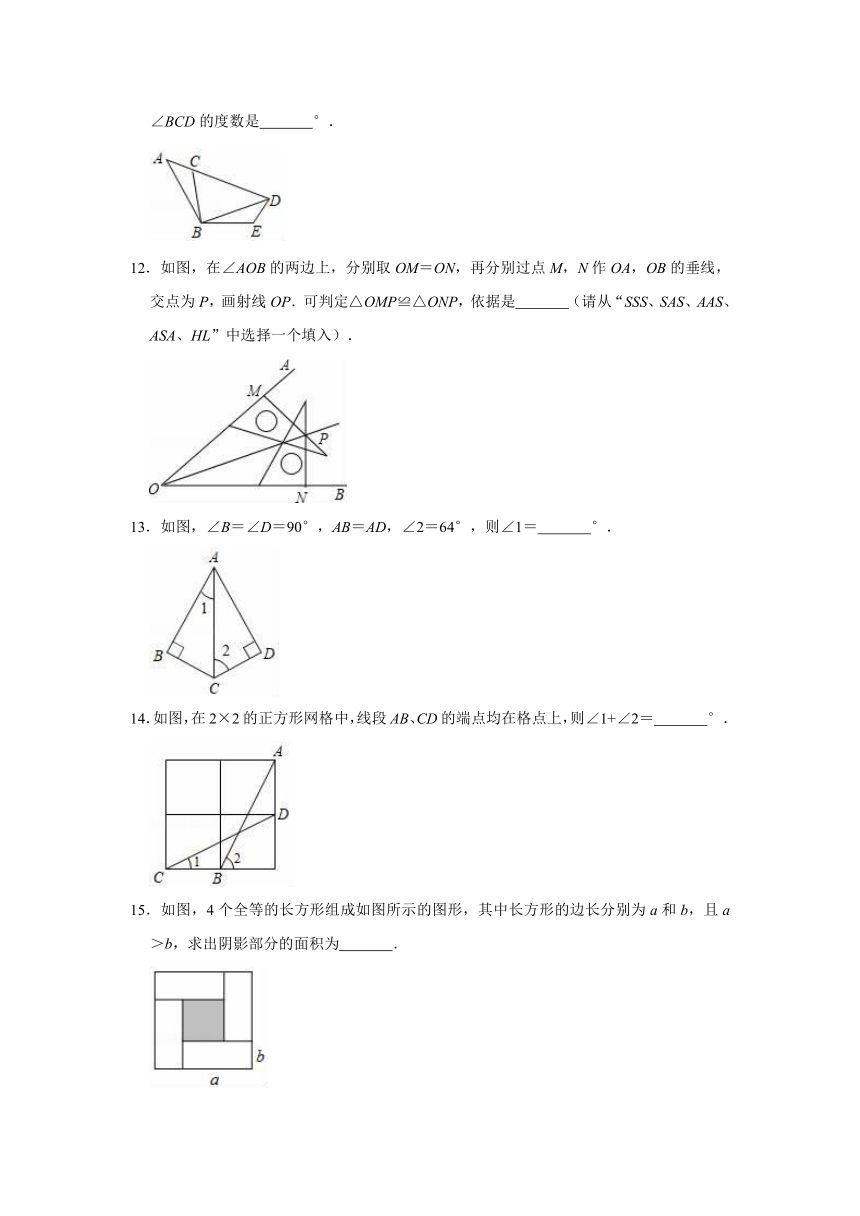
11.如图,已知△ABC≌△DBE,点D恰好在AC的延长线上,∠DBE=20°,∠BDE=41°.则∠BCD的度数是
°.
12.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP.可判定△OMP≌△ONP,依据是
(请从“SSS、SAS、AAS、ASA、HL”中选择一个填入).
13.如图,∠B=∠D=90°,AB=AD,∠2=64°,则∠1=
°.
14.如图,在2×2的正方形网格中,线段AB、CD的端点均在格点上,则∠1+∠2=
°.
15.如图,4个全等的长方形组成如图所示的图形,其中长方形的边长分别为a和b,且a>b,求出阴影部分的面积为
.
16.如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为
.
17.两个锐角分别相等的直角三角形
全等.(填“一定”或“不一定”或“一定不”)
18.如图,正方形网格中,点A,B,C,D均在格点上,则∠ACD+∠BDC=
°.
19.有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为
m.
20.三个正方形A、B、C按如图放置,若正方形A、C的面积分别为5,11,则正方形B的面积是
.
三.解答题
21.如图所示,已知∠B=∠D,点C在AB上,且AD=CB,CD=EB.求证:∠ACD=∠E.
22.如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.
要求:
(1)画出设计的测量示意图;
(2)写出测量方案及理由.
23.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)求证:AE=CF.
24.如图,已知点B,C,D,E在同一条直线上,AB=FC,AD=FE,BC=DE.求证:△ABD≌△FCE.
25.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
26.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,请你运用自己所学知识说明他们的做法是正确的.
参考答案与试题解析
一.选择题
1.解:A、两块三角尺不是全等形,故此选项不合题意;
B、两枚硬币不是全等形,故此选项不合题意;
C、两张A4纸是全等形,故此选项符合题意;
D、两片枫树叶不是全等形,故此选项不合题意;
故选:C.
2.解:平移前后两个图形是全等图形,对应点连线平行且相等.
故选:C.
3.解:在△ABD中,∠A=50°,∠ABD=38°,
∴∠ADB=180°﹣∠A﹣∠ABD=92°,
∵△AEC≌△ADB,
∴∠AEC=∠ADB=92°,
故选:B.
4.解;∵△ABC≌△A′B′C,
∴∠B=∠B′,∠ACB=∠A′CB′,
∴∠ACB﹣∠ACB′=∠A′CB′﹣∠ACB′,即∠ACA′=∠BCB′,
∵∠B=∠B′,∠BEC=∠B′EF,
∴∠B′FE=∠BCB′,
∵∠B′FE=∠AFG,
∴∠AFG=∠BCB′,
综上所述,与∠BCB′相等的角有3个,
故选:C.
5.解:①4、6是夹30°角的边时,可作1个三角形,
②4是30°角的对边时,可作2个三角形,
③6是30°角的对边时,可作1个三角形,
根据全等三角形的判定方法,以上三角形都是不全等的三角形,
所以,不全等的三角形共有4个.
故选:D.
6.解:∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°,
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL).
故选:A.
7.证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
故选:D.
8.解:∵AC⊥OA,BC⊥OB,
∴∠A=∠B=90°,
在Rt△AOC和Rt△BOC中,
∴Rt△AOC≌Rt△BOC(HL),
故选:D.
9.解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:AC﹣AB<AE<AC+AB,
∴2<AE<12,
∵AE=2AD,
∴1<AD<6,
故选:C.
10.解:A、根据SAS可以判定三角形全等,本选项不符合题意.
B、AA不能判定三角形全等,本选项符合题意.
C、根据HL可以判定三角形全等,本选项不符合题意.
D、根据AAS可以判定三角形全等,本选项不符合题意.
故选:B.
二.填空题
11.解:在△BDE中,∠DBE=20°,∠BDE=41°,
∴∠E=180°﹣∠DBE﹣∠BDE=119°,
∵△ABC≌△DBE,
∴∠ACB=∠E=119°,
∴∠BCD=180°﹣119°=61°,
故答案为:61.
12.解:由作法得OM=ON,PM⊥OM,PN⊥OB,
∴∠PMO=∠PNO=90°,
在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL).
故答案为“HL”.
13.解:∵∠B=∠D=90°,
在Rt△ABC与Rt△ADC中,,
∴Rt△ABC≌Rt△ADC(HL),
∴∠ACB=∠2=64°,
∴∠1=90°﹣∠ACB=90°﹣64°=26°,
故答案为:26.
14.解:由题意可得CO=AO,BO=DO,
在△COD和△AOB中,
∴△COD≌△AOB(SAS),
∴∠1=∠BAO,
∵∠2+∠BAO=90°,
∴∠1+∠2=90°.
故答案为:90.
15.解:∵如图所示的图形是4个全等的长方形组成的图形,
∴阴影部分的边长为a﹣b的正方形,
∴阴影部分的面积=(a﹣b)2,
故答案为:(a﹣b)2.
16.解:设BE=3t,则BF=7t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=60,
∴7t=60﹣3t,
解得:t=6,
∴AG=BE=3t=3×6=18;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=60,
∴3t=60﹣3t,
解得:t=10,
∴AG=BF=7t=7×10=70,
综上所述,AG=18或AG=70.
故答案为:18或70.
17.解:当还有一条边对应相等时,两直角三角形全等;
当三角形的边不相等时,两直角三角形不全等;
即两个锐角分别相等的直角三角形不一定全等,
故答案为:不一定.
18.解:在Rt△AEC和Rt△DAB中
∴Rt△AEC≌Rt△DAB(HL),
∴∠ACE=∠ABD,
∵∠EAC+∠ACE=90°,
∴∠EAC+∠ABD=90°,
∴∠AFB=90°,即∠CFD=90°,
∴∠ACD+∠BDC=90°,
故答案为90.
19.解:在△ABC和△EDC中,
∴△ABC≌△EDC(SAS),
∴AB=DE=800.
答:A,B之间的距离为800m.
故答案是:800.
20.解:如图,
∵A、B、C都是正方形,
∴DF=FH,∠DFH=∠DEF=∠FGH=90°;
∵∠DFE+∠HFG=∠EDF+∠DFE=90°,
∴∠EDF=∠HFG,
在△DEF和△FGH中,,
∴△DEF≌△FGH(AAS),
∴DE=FG,EF=GH;
在Rt△DEF中,由勾股定理得:DF2=DE2+EF2=DE2+GH2,
即SB=SA+SC=5+11=16,
故答案为:16.
三.解答题
21.证明:在△ACD与△ECB中,,
∴△ACD≌△ECB(SAS),
∴∠ACD=∠E.
22.解:(1)①如图所示;
分别以点A、点B为端点,作AQ、BP,
使其相交于点C,
使得CP=CB,CQ=CA,连接PQ,
测得PQ即可得出AB的长度.
②如图,
作BC⊥AC,测量出AC、BC的长,利用勾股定理求解可得.
(2)理由:由上面可知:PC=BC,QC=AC,
又∠PCQ=∠BCA,
∴在△PCQ与△BCA中,
,
∴△PCQ≌△BCA(SAS),
∴AB=PQ.
23.(1)解:∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠D+∠DCF=70°;
(2)证明:∵△ABF≌△CDE,
∴∠AFB=∠CED,AF=CE,
在△AFE和△CEF中,
,
∴△AFE≌△CEF(SAS),
∴AE=CF.
24.证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD和△FCE中,
,
∴△ABD≌△FCE
(SSS).
25.解:△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS).
26.证明:∵BF⊥AB,DE⊥BD,
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA),
∴DE=BA.
全等三角形》单元测试卷
一.选择题
1.下列各组中的两个图形为全等形的是( )
A.两块三角尺
B.两枚硬币
C.两张A4纸
D.两片枫树叶
2.平移前后两个图形是全等图形,对应点连线( )
A.平行但不相等
B.不平行也不相等
C.平行且相等
D.不相等
3.如图,△AEC≌△ADB,若∠A=50°,∠ABD=38°,则图中∠AEC的度数是( )
A.88°
B.92°
C.95°
D.102°
4.如图,△ABC≌△A′B′C,则图中所有角中与∠BCB′相等的角(除∠BCB′外)共有( )
A.1个
B.2个
C.3个
D.4个
5.一个三角形中,已知一个角为30°,两条边长为4和6,符合条件且互不全等的三角形有( )个.
A.1个
B.2个
C.3个
D.4个
6.如图,AC⊥BC,BD⊥AD,AC=BD,则判定△ABC与△BAD全等的依据是( )
A.HL
B.SAS
C.ASA
D.AAS
7.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS
B.AAS
C.ASA
D.SAS
8.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS
B.ASA
C.SAS
D.HL
9.在△ABC中,AB=5,AC=7,则中线AD的取值范围是( )
A.1<AD<7
B.1<AD<8
C.1<AD<6
D.2<AD<5
10.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.斜边和一直角边对应相等
D.斜边和一锐角对应相等
二.填空题
11.如图,已知△ABC≌△DBE,点D恰好在AC的延长线上,∠DBE=20°,∠BDE=41°.则∠BCD的度数是
°.
12.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP.可判定△OMP≌△ONP,依据是
(请从“SSS、SAS、AAS、ASA、HL”中选择一个填入).
13.如图,∠B=∠D=90°,AB=AD,∠2=64°,则∠1=
°.
14.如图,在2×2的正方形网格中,线段AB、CD的端点均在格点上,则∠1+∠2=
°.
15.如图,4个全等的长方形组成如图所示的图形,其中长方形的边长分别为a和b,且a>b,求出阴影部分的面积为
.
16.如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为
.
17.两个锐角分别相等的直角三角形
全等.(填“一定”或“不一定”或“一定不”)
18.如图,正方形网格中,点A,B,C,D均在格点上,则∠ACD+∠BDC=
°.
19.有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为
m.
20.三个正方形A、B、C按如图放置,若正方形A、C的面积分别为5,11,则正方形B的面积是
.
三.解答题
21.如图所示,已知∠B=∠D,点C在AB上,且AD=CB,CD=EB.求证:∠ACD=∠E.
22.如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.
要求:
(1)画出设计的测量示意图;
(2)写出测量方案及理由.
23.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)求证:AE=CF.
24.如图,已知点B,C,D,E在同一条直线上,AB=FC,AD=FE,BC=DE.求证:△ABD≌△FCE.
25.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
26.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,请你运用自己所学知识说明他们的做法是正确的.
参考答案与试题解析
一.选择题
1.解:A、两块三角尺不是全等形,故此选项不合题意;
B、两枚硬币不是全等形,故此选项不合题意;
C、两张A4纸是全等形,故此选项符合题意;
D、两片枫树叶不是全等形,故此选项不合题意;
故选:C.
2.解:平移前后两个图形是全等图形,对应点连线平行且相等.
故选:C.
3.解:在△ABD中,∠A=50°,∠ABD=38°,
∴∠ADB=180°﹣∠A﹣∠ABD=92°,
∵△AEC≌△ADB,
∴∠AEC=∠ADB=92°,
故选:B.
4.解;∵△ABC≌△A′B′C,
∴∠B=∠B′,∠ACB=∠A′CB′,
∴∠ACB﹣∠ACB′=∠A′CB′﹣∠ACB′,即∠ACA′=∠BCB′,
∵∠B=∠B′,∠BEC=∠B′EF,
∴∠B′FE=∠BCB′,
∵∠B′FE=∠AFG,
∴∠AFG=∠BCB′,
综上所述,与∠BCB′相等的角有3个,
故选:C.
5.解:①4、6是夹30°角的边时,可作1个三角形,
②4是30°角的对边时,可作2个三角形,
③6是30°角的对边时,可作1个三角形,
根据全等三角形的判定方法,以上三角形都是不全等的三角形,
所以,不全等的三角形共有4个.
故选:D.
6.解:∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°,
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL).
故选:A.
7.证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
故选:D.
8.解:∵AC⊥OA,BC⊥OB,
∴∠A=∠B=90°,
在Rt△AOC和Rt△BOC中,
∴Rt△AOC≌Rt△BOC(HL),
故选:D.
9.解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:AC﹣AB<AE<AC+AB,
∴2<AE<12,
∵AE=2AD,
∴1<AD<6,
故选:C.
10.解:A、根据SAS可以判定三角形全等,本选项不符合题意.
B、AA不能判定三角形全等,本选项符合题意.
C、根据HL可以判定三角形全等,本选项不符合题意.
D、根据AAS可以判定三角形全等,本选项不符合题意.
故选:B.
二.填空题
11.解:在△BDE中,∠DBE=20°,∠BDE=41°,
∴∠E=180°﹣∠DBE﹣∠BDE=119°,
∵△ABC≌△DBE,
∴∠ACB=∠E=119°,
∴∠BCD=180°﹣119°=61°,
故答案为:61.
12.解:由作法得OM=ON,PM⊥OM,PN⊥OB,
∴∠PMO=∠PNO=90°,
在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL).
故答案为“HL”.
13.解:∵∠B=∠D=90°,
在Rt△ABC与Rt△ADC中,,
∴Rt△ABC≌Rt△ADC(HL),
∴∠ACB=∠2=64°,
∴∠1=90°﹣∠ACB=90°﹣64°=26°,
故答案为:26.
14.解:由题意可得CO=AO,BO=DO,
在△COD和△AOB中,
∴△COD≌△AOB(SAS),
∴∠1=∠BAO,
∵∠2+∠BAO=90°,
∴∠1+∠2=90°.
故答案为:90.
15.解:∵如图所示的图形是4个全等的长方形组成的图形,
∴阴影部分的边长为a﹣b的正方形,
∴阴影部分的面积=(a﹣b)2,
故答案为:(a﹣b)2.
16.解:设BE=3t,则BF=7t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=60,
∴7t=60﹣3t,
解得:t=6,
∴AG=BE=3t=3×6=18;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=60,
∴3t=60﹣3t,
解得:t=10,
∴AG=BF=7t=7×10=70,
综上所述,AG=18或AG=70.
故答案为:18或70.
17.解:当还有一条边对应相等时,两直角三角形全等;
当三角形的边不相等时,两直角三角形不全等;
即两个锐角分别相等的直角三角形不一定全等,
故答案为:不一定.
18.解:在Rt△AEC和Rt△DAB中
∴Rt△AEC≌Rt△DAB(HL),
∴∠ACE=∠ABD,
∵∠EAC+∠ACE=90°,
∴∠EAC+∠ABD=90°,
∴∠AFB=90°,即∠CFD=90°,
∴∠ACD+∠BDC=90°,
故答案为90.
19.解:在△ABC和△EDC中,
∴△ABC≌△EDC(SAS),
∴AB=DE=800.
答:A,B之间的距离为800m.
故答案是:800.
20.解:如图,
∵A、B、C都是正方形,
∴DF=FH,∠DFH=∠DEF=∠FGH=90°;
∵∠DFE+∠HFG=∠EDF+∠DFE=90°,
∴∠EDF=∠HFG,
在△DEF和△FGH中,,
∴△DEF≌△FGH(AAS),
∴DE=FG,EF=GH;
在Rt△DEF中,由勾股定理得:DF2=DE2+EF2=DE2+GH2,
即SB=SA+SC=5+11=16,
故答案为:16.
三.解答题
21.证明:在△ACD与△ECB中,,
∴△ACD≌△ECB(SAS),
∴∠ACD=∠E.
22.解:(1)①如图所示;
分别以点A、点B为端点,作AQ、BP,
使其相交于点C,
使得CP=CB,CQ=CA,连接PQ,
测得PQ即可得出AB的长度.
②如图,
作BC⊥AC,测量出AC、BC的长,利用勾股定理求解可得.
(2)理由:由上面可知:PC=BC,QC=AC,
又∠PCQ=∠BCA,
∴在△PCQ与△BCA中,
,
∴△PCQ≌△BCA(SAS),
∴AB=PQ.
23.(1)解:∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠D+∠DCF=70°;
(2)证明:∵△ABF≌△CDE,
∴∠AFB=∠CED,AF=CE,
在△AFE和△CEF中,
,
∴△AFE≌△CEF(SAS),
∴AE=CF.
24.证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD和△FCE中,
,
∴△ABD≌△FCE
(SSS).
25.解:△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS).
26.证明:∵BF⊥AB,DE⊥BD,
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA),
∴DE=BA.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
