北师大版九年级数学下册第一章1 锐角三角函数 1.1正切同步练习题(word含答案)
文档属性
| 名称 | 北师大版九年级数学下册第一章1 锐角三角函数 1.1正切同步练习题(word含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 443.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 06:48:26 | ||
图片预览



文档简介
北师大版九年级数学下第一章1
锐角三角函数
1.1正切练习题(含答案)
一、选择题
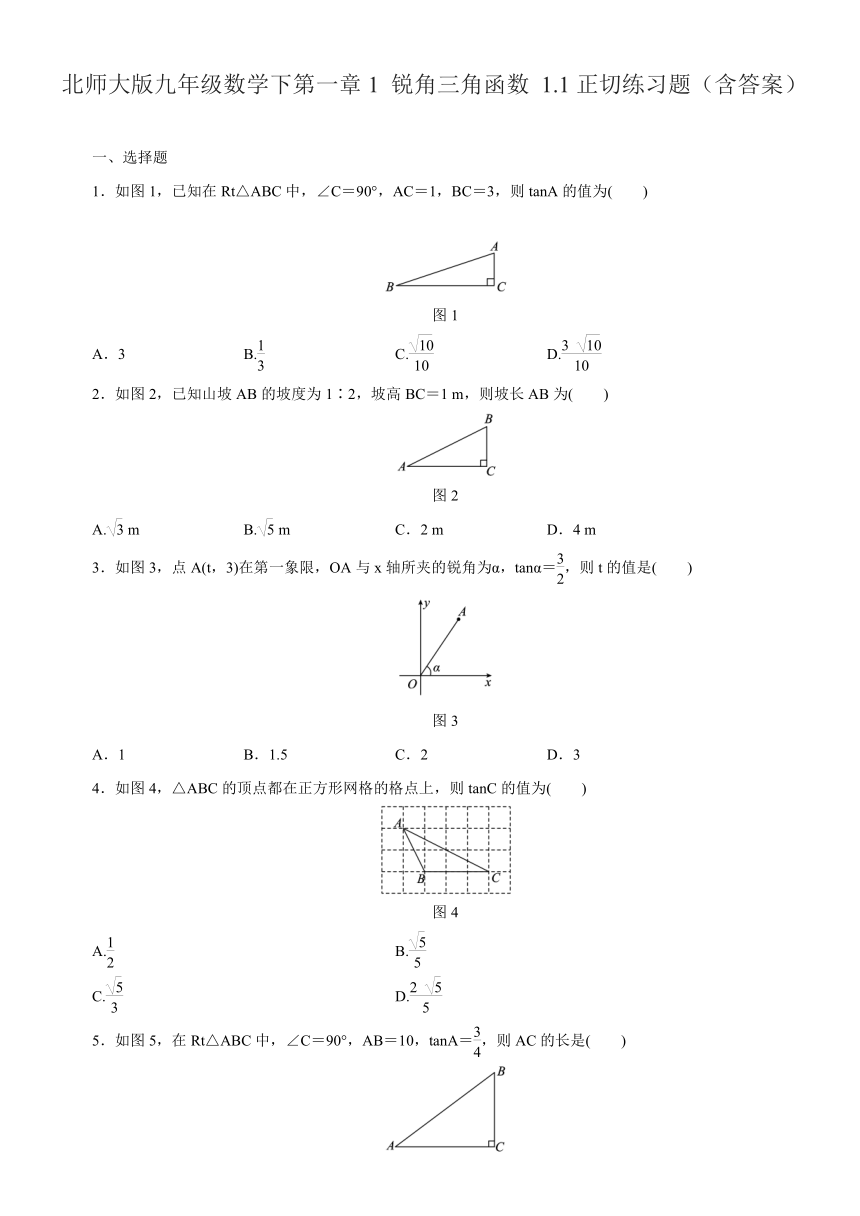
1.如图1,已知在Rt△ABC中,∠C=90°,AC=1,BC=3,则tanA的值为( )
图1
A.3
B.
C.
D.
2.如图2,已知山坡AB的坡度为1∶2,坡高BC=1
m,则坡长AB为( )
图2
A.
m
B.
m
C.2
m
D.4
m
3.如图3,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是( )
图3
A.1
B.1.5
C.2
D.3
4.如图4,△ABC的顶点都在正方形网格的格点上,则tanC的值为( )
图4
A.
B.
C.
D.
5.如图5,在Rt△ABC中,∠C=90°,AB=10,tanA=,则AC的长是( )
图5
A.3
B.4
C.6
D.8
6.如图6所示,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,已知CD=5,AC=6,则tanB的值为( )
图6
A.
B.
C.
D.
7.直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图7中所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
图7
A.
B.
C.
D.
二、填空题
8.在Rt△ABC中,∠C=90°,若△ABC各边的长度同时扩大为原来的10倍,则tanA的值________.(填“变大”“不变”或“变小”)
9.如图8,一座公路桥离地面的高度AC为6米,引桥AB的水平宽度BC为24米,为降低坡度,现决定将引桥坡面改为AD,使其坡度为1∶6,则BD的长是________.
图8
三、解答题
10.如图9,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,求tan∠BCD的值.
图9
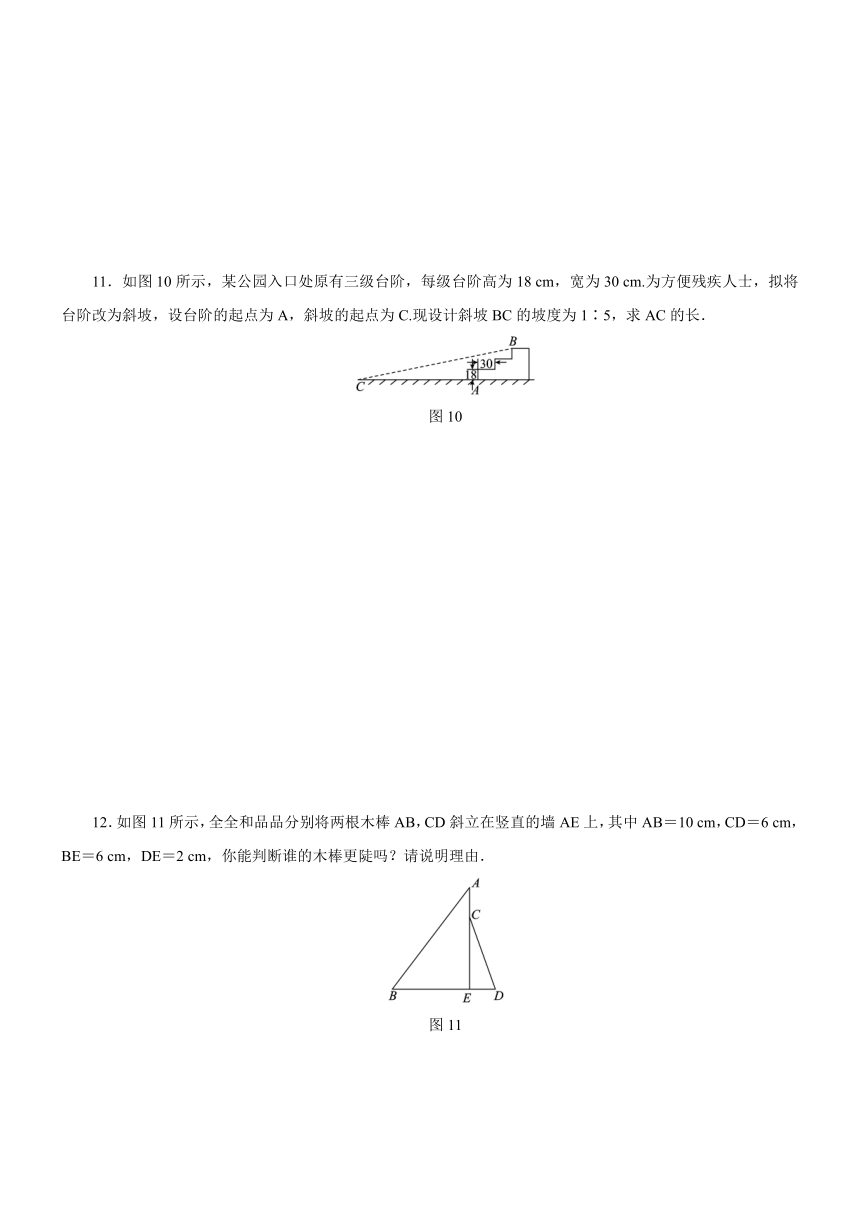
11.如图10所示,某公园入口处原有三级台阶,每级台阶高为18
cm,宽为30
cm.为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C.现设计斜坡BC的坡度为1∶5,求AC的长.
图10
12.如图11所示,全全和品品分别将两根木棒AB,CD斜立在竖直的墙AE上,其中AB=10
cm,CD=6
cm,BE=6
cm,DE=2
cm,你能判断谁的木棒更陡吗?请说明理由.
图11
附加题
1.如图12,在Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,则tan∠BAO的值为________.
图12
2.数学老师布置了这样一个问题:
如果α,β都为锐角,且tanα=,tanβ=,求α+β的度数.
甲、乙两名同学想利用正方形网格图来解决这个问题,他们分别设计了图13①和②.
(1)请你分别利用图①、图②求出α+β的度数;
(2)请参考以上解决问题的方法,选择一种方法解决下面的问题:
如果α,β都为锐角,当tanα=5,tanβ=时,在图③的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β,并求出α-β的度数.
图13
参考答案
1.[答案]
A
2.[解析]
B ∵山坡AB的坡度为i=1∶2,坡高BC=1
m,∴=,∴AC=2
m.根据勾股定理,得AB===(m).故选B.
3.[解析]
C 过点A作AB⊥x轴于点B.
∵点A(t,3)在第一象限,∴AB=3,OB=t.
又∵tanα==,∴t=2.
4.[答案]
A
5.[解析]
D 因为tanA==,
所以设BC=3x,AC=4x(x>0).由勾股定理,得BC2+AC2=AB2,即(3x)2+(4x)2=100,解得x=2,所以AC=4x=4×2=8.故选D.
6.[解析]
C ∵CD是斜边AB上的中线,CD=5,∴AB=2CD=10.
在Rt△ABC中,根据勾股定理,得BC===8,
∴tanB===.故选C.
7.[解析]
C 设CE=x,根据折叠的性质,得BE=AE=8-x.在Rt△BCE中,根据勾股定理列出关于x的方程,得x2+62=(8-x)2,解得x=(负值已舍去),即可计算出tan∠CBE=.
8.[答案]
不变
9.[答案]
12米
10.解:∵∠ACB=90°,AB=5,BC=3,
∴AC==4.
∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠B=90°,∠A+∠B=90°,
∴∠A=∠BCD,
∴tan∠BCD=tanA==.
11.解:如图,过点B作BD⊥AC于点D.依题意可求得AD=60
cm,BD=54
cm.因为斜坡BC的坡度i=1∶5,所以=,所以CD=270
cm,故AC=CD-AD=270-60=210(cm).
12.解:能.品品的木棒CD更陡.
理由:∵AB=10
cm,BE=6
cm,∠AEB=90°,
∴AE==8
cm,
∴tanB==.
∵CD=6
cm,DE=2
cm,∠CED=90°,
∴CE==4
cm,
∴tanD===2
.
∵<2
,即tanB∴品品的木棒CD更陡.
附加题
1.[答案]
[解析]
过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
则∠BDO=∠ACO=90°.
∵顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,
∴S△BDO=,S△OCA=.
∵∠BDO=∠AOB=90°,
∴∠BOD+∠DBO=∠BOD+∠AOC=90°,
∴∠DBO=∠AOC,∴△BDO∽△OCA,
∴=()2==5,
∴=,∴tan∠BAO==.
故答案为.
2.解:(1)如图①.
在△AMC和△CNB中,
∵AM=CN,∠AMC=∠CNB=90°,MC=NB,
∴△AMC≌△CNB,
∴AC=CB,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,
∴∠ACM+∠BCN=90°,
∴∠ACB=90°,
∴∠CAB=∠CBA=45°,
即α+β=45°.
如图②,连接BE.设每个小正方形的边长均为1,
则CE=1,AE=2,BE=,
∴==,=,
∴=.
又∵∠CEB=∠BEA,
∴△CEB∽△BEA,
∴∠CBE=∠BAE=α,
∴∠BED=∠CBE+∠ECB=α+β.
∵DE=DB,∠D=90°,
∴∠BED=45°,
∴α+β=45°.
(2)如图③,∠MOE=α,∠NOH=β,∠MON=α-β.
在△MFN和△NHO中,
∵MF=NH,∠MFN=∠NHO=90°,FN=HO,
∴△MFN≌△NHO,
∴MN=NO,∠MNF=∠NOH.
∵∠NOH+∠ONH=90°,
∴∠ONH+∠MNF=90°,
∴∠MNO=90°,
∴∠MON=∠NMO=45°,
即α-β=45°.
锐角三角函数
1.1正切练习题(含答案)
一、选择题
1.如图1,已知在Rt△ABC中,∠C=90°,AC=1,BC=3,则tanA的值为( )
图1
A.3
B.
C.
D.
2.如图2,已知山坡AB的坡度为1∶2,坡高BC=1
m,则坡长AB为( )
图2
A.
m
B.
m
C.2
m
D.4
m
3.如图3,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是( )
图3
A.1
B.1.5
C.2
D.3
4.如图4,△ABC的顶点都在正方形网格的格点上,则tanC的值为( )
图4
A.
B.
C.
D.
5.如图5,在Rt△ABC中,∠C=90°,AB=10,tanA=,则AC的长是( )
图5
A.3
B.4
C.6
D.8
6.如图6所示,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,已知CD=5,AC=6,则tanB的值为( )
图6
A.
B.
C.
D.
7.直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图7中所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
图7
A.
B.
C.
D.
二、填空题
8.在Rt△ABC中,∠C=90°,若△ABC各边的长度同时扩大为原来的10倍,则tanA的值________.(填“变大”“不变”或“变小”)
9.如图8,一座公路桥离地面的高度AC为6米,引桥AB的水平宽度BC为24米,为降低坡度,现决定将引桥坡面改为AD,使其坡度为1∶6,则BD的长是________.
图8
三、解答题
10.如图9,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,求tan∠BCD的值.
图9
11.如图10所示,某公园入口处原有三级台阶,每级台阶高为18
cm,宽为30
cm.为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C.现设计斜坡BC的坡度为1∶5,求AC的长.
图10
12.如图11所示,全全和品品分别将两根木棒AB,CD斜立在竖直的墙AE上,其中AB=10
cm,CD=6
cm,BE=6
cm,DE=2
cm,你能判断谁的木棒更陡吗?请说明理由.
图11
附加题
1.如图12,在Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,则tan∠BAO的值为________.
图12
2.数学老师布置了这样一个问题:
如果α,β都为锐角,且tanα=,tanβ=,求α+β的度数.
甲、乙两名同学想利用正方形网格图来解决这个问题,他们分别设计了图13①和②.
(1)请你分别利用图①、图②求出α+β的度数;
(2)请参考以上解决问题的方法,选择一种方法解决下面的问题:
如果α,β都为锐角,当tanα=5,tanβ=时,在图③的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β,并求出α-β的度数.
图13
参考答案
1.[答案]
A
2.[解析]
B ∵山坡AB的坡度为i=1∶2,坡高BC=1
m,∴=,∴AC=2
m.根据勾股定理,得AB===(m).故选B.
3.[解析]
C 过点A作AB⊥x轴于点B.
∵点A(t,3)在第一象限,∴AB=3,OB=t.
又∵tanα==,∴t=2.
4.[答案]
A
5.[解析]
D 因为tanA==,
所以设BC=3x,AC=4x(x>0).由勾股定理,得BC2+AC2=AB2,即(3x)2+(4x)2=100,解得x=2,所以AC=4x=4×2=8.故选D.
6.[解析]
C ∵CD是斜边AB上的中线,CD=5,∴AB=2CD=10.
在Rt△ABC中,根据勾股定理,得BC===8,
∴tanB===.故选C.
7.[解析]
C 设CE=x,根据折叠的性质,得BE=AE=8-x.在Rt△BCE中,根据勾股定理列出关于x的方程,得x2+62=(8-x)2,解得x=(负值已舍去),即可计算出tan∠CBE=.
8.[答案]
不变
9.[答案]
12米
10.解:∵∠ACB=90°,AB=5,BC=3,
∴AC==4.
∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠B=90°,∠A+∠B=90°,
∴∠A=∠BCD,
∴tan∠BCD=tanA==.
11.解:如图,过点B作BD⊥AC于点D.依题意可求得AD=60
cm,BD=54
cm.因为斜坡BC的坡度i=1∶5,所以=,所以CD=270
cm,故AC=CD-AD=270-60=210(cm).
12.解:能.品品的木棒CD更陡.
理由:∵AB=10
cm,BE=6
cm,∠AEB=90°,
∴AE==8
cm,
∴tanB==.
∵CD=6
cm,DE=2
cm,∠CED=90°,
∴CE==4
cm,
∴tanD===2
.
∵<2
,即tanB
附加题
1.[答案]
[解析]
过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
则∠BDO=∠ACO=90°.
∵顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,
∴S△BDO=,S△OCA=.
∵∠BDO=∠AOB=90°,
∴∠BOD+∠DBO=∠BOD+∠AOC=90°,
∴∠DBO=∠AOC,∴△BDO∽△OCA,
∴=()2==5,
∴=,∴tan∠BAO==.
故答案为.
2.解:(1)如图①.
在△AMC和△CNB中,
∵AM=CN,∠AMC=∠CNB=90°,MC=NB,
∴△AMC≌△CNB,
∴AC=CB,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,
∴∠ACM+∠BCN=90°,
∴∠ACB=90°,
∴∠CAB=∠CBA=45°,
即α+β=45°.
如图②,连接BE.设每个小正方形的边长均为1,
则CE=1,AE=2,BE=,
∴==,=,
∴=.
又∵∠CEB=∠BEA,
∴△CEB∽△BEA,
∴∠CBE=∠BAE=α,
∴∠BED=∠CBE+∠ECB=α+β.
∵DE=DB,∠D=90°,
∴∠BED=45°,
∴α+β=45°.
(2)如图③,∠MOE=α,∠NOH=β,∠MON=α-β.
在△MFN和△NHO中,
∵MF=NH,∠MFN=∠NHO=90°,FN=HO,
∴△MFN≌△NHO,
∴MN=NO,∠MNF=∠NOH.
∵∠NOH+∠ONH=90°,
∴∠ONH+∠MNF=90°,
∴∠MNO=90°,
∴∠MON=∠NMO=45°,
即α-β=45°.
