北师大版八年级数学上册《4.4 一次函数的应用》 同步练习卷(word版 含答案)
文档属性
| 名称 | 北师大版八年级数学上册《4.4 一次函数的应用》 同步练习卷(word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 11:21:08 | ||
图片预览



文档简介
4.4
一次函数的应用
一.选择题
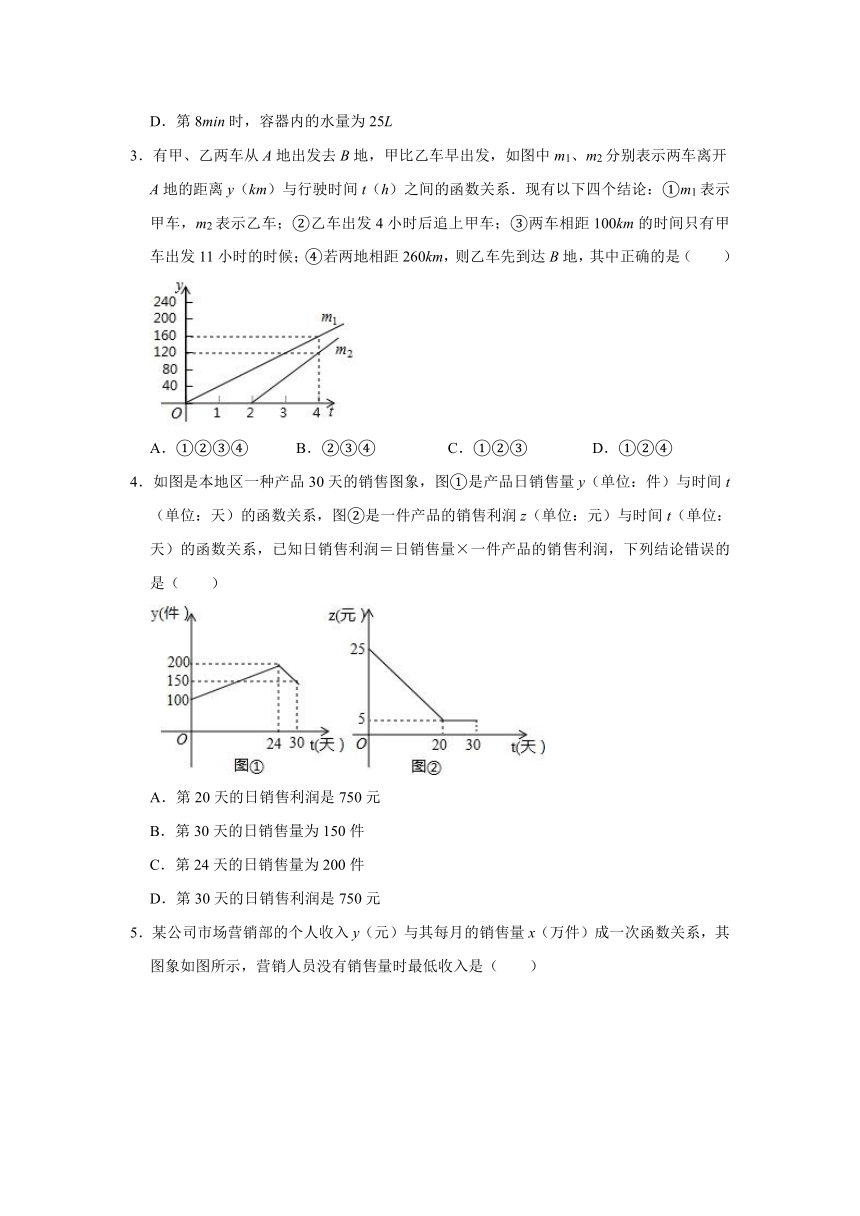
1.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.下列四种说法:其中正确的个数是( )
①每分钟的进水量为5升.
②每分钟的出水量为3.75升.
③从计时开始8分钟时,容器内的水量为25升.
④容器从进水开始到水全部放完的时间是20分钟.
A.1个
B.2个
C.3个
D.4个
2.一个有进水管与出水管的容器,从某时刻开始的4min内只进水不出水,在随后的8min内既进水又出水,每min的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.根据图象提供的信息,则下列结论错误的是( )
A.第4min时,容器内的水量为20L
B.每min进水量为5L
C.每min出水量为1.25L
D.第8min时,容器内的水量为25L
3.有甲、乙两车从A地出发去B地,甲比乙车早出发,如图中m1、m2分别表示两车离开A地的距离y(km)与行驶时间t(h)之间的函数关系.现有以下四个结论:①m1表示甲车,m2表示乙车;②乙车出发4小时后追上甲车;③两车相距100km的时间只有甲车出发11小时的时候;④若两地相距260km,则乙车先到达B地,其中正确的是( )
A.①②③④
B.②③④
C.①②③
D.①②④
4.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
A.第20天的日销售利润是750元
B.第30天的日销售量为150件
C.第24天的日销售量为200件
D.第30天的日销售利润是750元
5.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
6.如图,线段OA,BA分别表示甲、乙两名学生运动的路程S与时间t的关系,根据图象可得,快者比慢者每秒多跑( )
A.25米
B.6.25米
C.5米
D.1.25米
7.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为y元).方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为( )
A.80
B.120
C.160
D.200
8.星期天早晨,小广,小雅两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,小广到达B地后立即以另一速度按原路返回,如图是两人离A地的距离y(米)与小雅运动的时间x(分)之间的函数图象,则下列说错误的是( )
A.小广返回到A地时,小雅还需要8分钟到达A地
B.整个运动过程中,他们遇见了2次
C.A、B两地相距3000米
D.小广去时的速度小于返回时的速度
9.小明用刻度不超过100℃的温度计来估计某食用油的沸点温度:将该食用油倒入锅中,均匀加热,每隔10s测量一次锅中的油温,得到如下数据:
时间t(单位:S)
0
10
20
30
40
油温y(单位:℃)
10
30
50
70
90
当加热100s时,油沸腾了,则小明估计这种油的沸点温度是( )
A.150℃
B.170℃
C.190℃
D.210℃
10.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )元.
A.3
B.4
C.5
D.6
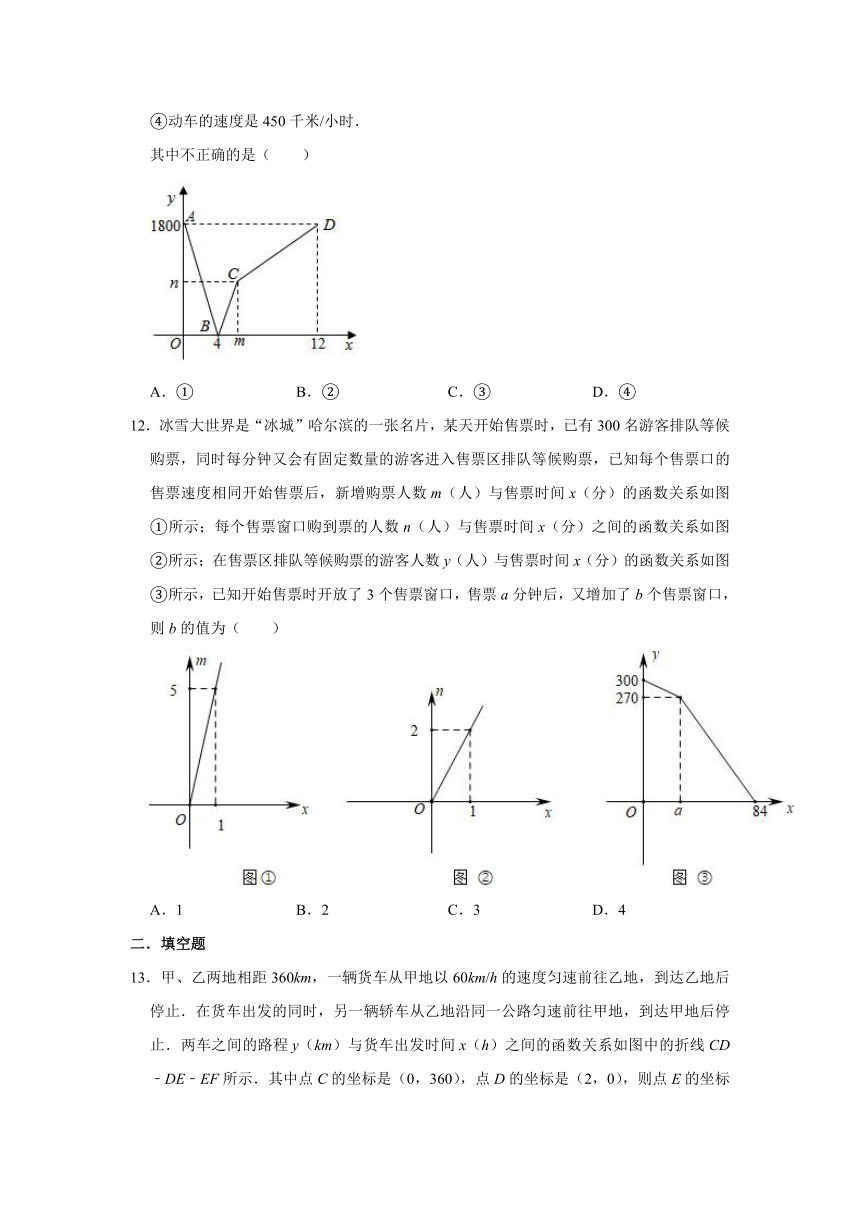
11.甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列说法:
①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③m=6,n=900;
④动车的速度是450千米/小时.
其中不正确的是( )
A.①
B.②
C.③
D.④
12.冰雪大世界是“冰城”哈尔滨的一张名片,某天开始售票时,已有300名游客排队等候购票,同时每分钟又会有固定数量的游客进入售票区排队等候购票,已知每个售票口的售票速度相同开始售票后,新增购票人数m(人)与售票时间x(分)的函数关系如图①所示;每个售票窗口购到票的人数n(人)与售票时间x(分)之间的函数关系如图②所示;在售票区排队等候购票的游客人数y(人)与售票时间x(分)的函数关系如图③所示,已知开始售票时开放了3个售票窗口,售票a分钟后,又增加了b个售票窗口,则b的值为( )
A.1
B.2
C.3
D.4
二.填空题
13.甲、乙两地相距360km,一辆货车从甲地以60km/h的速度匀速前往乙地,到达乙地后停止.在货车出发的同时,另一辆轿车从乙地沿同一公路匀速前往甲地,到达甲地后停止.两车之间的路程y(km)与货车出发时间x(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.其中点C的坐标是(0,360),点D的坐标是(2,0),则点E的坐标是
.
14.某衬衣定价为100元时,每月可卖出2000件,受成本影响,该衬衣需涨价,已知价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)之间的关系式为
.
15.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费y(元)与用水量x(吨)之间的函数关系如图所示.按上述分段收费标准,小明家三、四月份分别交水费29元和18元,则四月份比三月份节约用水
吨.
16.某公司行李托运的费用与重量的关系为一次函数,由如图可知只要重量不超过
千克,就可以免费托运.
17.甲、乙两名运动员在笔直的公路上进行骑自行车训练.如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,在两人行驶过程中,当t=
小时时,甲、乙两名运动员相距12千米.
18.小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行
米.
19.如图,直线y=﹣x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标
;
(2)若△OQC是等腰直角三角形,则t的值为
;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数关系式
.
20.如图,在平面直角坐标系中,点A的坐标是(0,2),点B的坐标是(2,0),连结AB,点P是线段AB上的一个动点(包括两端点),直线y=﹣x上有一动点Q,连结OP,PQ,已知△OPQ的面积为,则点Q的坐标为
.
三.解答题
21.在直角坐标系中,点O是原点,已直线y=x+m(m>0)分别与x轴,y轴交于点A和B,点P(1,n)在AB上,过点P的直线与x轴交于点C(4,0),与y轴交于点D.
(1)当△PAC是直角三角形时,求点P的坐标;
(2)若直线OP∥AD,求m的值.
22.如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2).
(1)求直线AC的表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
参考答案
一.选择题
1.
D.
2.C
3.
A.
4.
A.
5.
B.
6.
D.
7.D.
8.
A.
9.
D.
10.
B.
11.
D.
12.
B.
二.填空题
13.(3,180).
14.y=﹣5x+2500.
15.
4.
16.
20.
17.
5.4.
18.
350.
19.(1)(2,2);(3)y=﹣2x+6.
20.(,﹣)或(﹣,).
三.解答题
21.对于y=x+m(m>0),令x=0,则y=m,令y=x+m=0,则x=﹣m,
故点A、B的坐标分别为(﹣m,0)、(0,m),
将点P的坐标代入y=x+m得:n=m+1,故点P(1,m+1),
(1)由点A、B的坐标知,直线AB与x轴的夹角为45°,
当△PAC是直角三角形时,则∠APC为直角,则∠PCA=45°.
设直线PC的表达式为y=﹣x+b,将点C的坐标代入上式得:0=﹣4+b,解得b=4,
故直线CP的表达式为y=﹣x+4,
当x=1时,y=﹣x+4=3,
故点P(1,3);
(2)设直线OP的表达式为y=kx,
将点P的坐标代入上式得:n=k,
即直线OP的表达式为y=nx,
同理直线PC的表达式为y=﹣n(x﹣4),
令x=0,则y=n,即点D(0,),
由点A、D的坐标同理可得,直线AD的表达式为y=(x+m),
∵OP∥AD,
∴n=,
解得m=.
22.(1)设直线AC的解析式是y=kx+b,
根据题意得:,
解得:.
则直线AC的解析式是:y=﹣x+6;
(2)∵C(0,6),A(4,2),
∴OC=6,
∴S△OAC=×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=.
则直线的解析式是:y=x,
∵当△OMC的面积是△OAC的面积的时,
∴M到y轴的距离是×4=1,
∴点M的横坐标为1或﹣1;
当M的横坐标是:1,
在y=x中,当x=1时,y=,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
当M的横坐标是:﹣1,
在y=﹣x+6中,当x=﹣1时,y=7,则M的坐标是(﹣1,7).
综上所述:M的坐标是:M1(1,)或M2(1,5)或M3(﹣1,7).
一次函数的应用
一.选择题
1.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.下列四种说法:其中正确的个数是( )
①每分钟的进水量为5升.
②每分钟的出水量为3.75升.
③从计时开始8分钟时,容器内的水量为25升.
④容器从进水开始到水全部放完的时间是20分钟.
A.1个
B.2个
C.3个
D.4个
2.一个有进水管与出水管的容器,从某时刻开始的4min内只进水不出水,在随后的8min内既进水又出水,每min的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.根据图象提供的信息,则下列结论错误的是( )
A.第4min时,容器内的水量为20L
B.每min进水量为5L
C.每min出水量为1.25L
D.第8min时,容器内的水量为25L
3.有甲、乙两车从A地出发去B地,甲比乙车早出发,如图中m1、m2分别表示两车离开A地的距离y(km)与行驶时间t(h)之间的函数关系.现有以下四个结论:①m1表示甲车,m2表示乙车;②乙车出发4小时后追上甲车;③两车相距100km的时间只有甲车出发11小时的时候;④若两地相距260km,则乙车先到达B地,其中正确的是( )
A.①②③④
B.②③④
C.①②③
D.①②④
4.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
A.第20天的日销售利润是750元
B.第30天的日销售量为150件
C.第24天的日销售量为200件
D.第30天的日销售利润是750元
5.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
6.如图,线段OA,BA分别表示甲、乙两名学生运动的路程S与时间t的关系,根据图象可得,快者比慢者每秒多跑( )
A.25米
B.6.25米
C.5米
D.1.25米
7.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为y元).方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为( )
A.80
B.120
C.160
D.200
8.星期天早晨,小广,小雅两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,小广到达B地后立即以另一速度按原路返回,如图是两人离A地的距离y(米)与小雅运动的时间x(分)之间的函数图象,则下列说错误的是( )
A.小广返回到A地时,小雅还需要8分钟到达A地
B.整个运动过程中,他们遇见了2次
C.A、B两地相距3000米
D.小广去时的速度小于返回时的速度
9.小明用刻度不超过100℃的温度计来估计某食用油的沸点温度:将该食用油倒入锅中,均匀加热,每隔10s测量一次锅中的油温,得到如下数据:
时间t(单位:S)
0
10
20
30
40
油温y(单位:℃)
10
30
50
70
90
当加热100s时,油沸腾了,则小明估计这种油的沸点温度是( )
A.150℃
B.170℃
C.190℃
D.210℃
10.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )元.
A.3
B.4
C.5
D.6
11.甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列说法:
①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③m=6,n=900;
④动车的速度是450千米/小时.
其中不正确的是( )
A.①
B.②
C.③
D.④
12.冰雪大世界是“冰城”哈尔滨的一张名片,某天开始售票时,已有300名游客排队等候购票,同时每分钟又会有固定数量的游客进入售票区排队等候购票,已知每个售票口的售票速度相同开始售票后,新增购票人数m(人)与售票时间x(分)的函数关系如图①所示;每个售票窗口购到票的人数n(人)与售票时间x(分)之间的函数关系如图②所示;在售票区排队等候购票的游客人数y(人)与售票时间x(分)的函数关系如图③所示,已知开始售票时开放了3个售票窗口,售票a分钟后,又增加了b个售票窗口,则b的值为( )
A.1
B.2
C.3
D.4
二.填空题
13.甲、乙两地相距360km,一辆货车从甲地以60km/h的速度匀速前往乙地,到达乙地后停止.在货车出发的同时,另一辆轿车从乙地沿同一公路匀速前往甲地,到达甲地后停止.两车之间的路程y(km)与货车出发时间x(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.其中点C的坐标是(0,360),点D的坐标是(2,0),则点E的坐标是
.
14.某衬衣定价为100元时,每月可卖出2000件,受成本影响,该衬衣需涨价,已知价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)之间的关系式为
.
15.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费y(元)与用水量x(吨)之间的函数关系如图所示.按上述分段收费标准,小明家三、四月份分别交水费29元和18元,则四月份比三月份节约用水
吨.
16.某公司行李托运的费用与重量的关系为一次函数,由如图可知只要重量不超过
千克,就可以免费托运.
17.甲、乙两名运动员在笔直的公路上进行骑自行车训练.如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,在两人行驶过程中,当t=
小时时,甲、乙两名运动员相距12千米.
18.小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行
米.
19.如图,直线y=﹣x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标
;
(2)若△OQC是等腰直角三角形,则t的值为
;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数关系式
.
20.如图,在平面直角坐标系中,点A的坐标是(0,2),点B的坐标是(2,0),连结AB,点P是线段AB上的一个动点(包括两端点),直线y=﹣x上有一动点Q,连结OP,PQ,已知△OPQ的面积为,则点Q的坐标为
.
三.解答题
21.在直角坐标系中,点O是原点,已直线y=x+m(m>0)分别与x轴,y轴交于点A和B,点P(1,n)在AB上,过点P的直线与x轴交于点C(4,0),与y轴交于点D.
(1)当△PAC是直角三角形时,求点P的坐标;
(2)若直线OP∥AD,求m的值.
22.如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2).
(1)求直线AC的表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
参考答案
一.选择题
1.
D.
2.C
3.
A.
4.
A.
5.
B.
6.
D.
7.D.
8.
A.
9.
D.
10.
B.
11.
D.
12.
B.
二.填空题
13.(3,180).
14.y=﹣5x+2500.
15.
4.
16.
20.
17.
5.4.
18.
350.
19.(1)(2,2);(3)y=﹣2x+6.
20.(,﹣)或(﹣,).
三.解答题
21.对于y=x+m(m>0),令x=0,则y=m,令y=x+m=0,则x=﹣m,
故点A、B的坐标分别为(﹣m,0)、(0,m),
将点P的坐标代入y=x+m得:n=m+1,故点P(1,m+1),
(1)由点A、B的坐标知,直线AB与x轴的夹角为45°,
当△PAC是直角三角形时,则∠APC为直角,则∠PCA=45°.
设直线PC的表达式为y=﹣x+b,将点C的坐标代入上式得:0=﹣4+b,解得b=4,
故直线CP的表达式为y=﹣x+4,
当x=1时,y=﹣x+4=3,
故点P(1,3);
(2)设直线OP的表达式为y=kx,
将点P的坐标代入上式得:n=k,
即直线OP的表达式为y=nx,
同理直线PC的表达式为y=﹣n(x﹣4),
令x=0,则y=n,即点D(0,),
由点A、D的坐标同理可得,直线AD的表达式为y=(x+m),
∵OP∥AD,
∴n=,
解得m=.
22.(1)设直线AC的解析式是y=kx+b,
根据题意得:,
解得:.
则直线AC的解析式是:y=﹣x+6;
(2)∵C(0,6),A(4,2),
∴OC=6,
∴S△OAC=×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=.
则直线的解析式是:y=x,
∵当△OMC的面积是△OAC的面积的时,
∴M到y轴的距离是×4=1,
∴点M的横坐标为1或﹣1;
当M的横坐标是:1,
在y=x中,当x=1时,y=,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
当M的横坐标是:﹣1,
在y=﹣x+6中,当x=﹣1时,y=7,则M的坐标是(﹣1,7).
综上所述:M的坐标是:M1(1,)或M2(1,5)或M3(﹣1,7).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
