3.1一元二次方程（第1课时）课件

(共21张PPT)
回顾思考：
1.什么叫方程？
2.什么叫一元一次方程？
3.什么叫分式方程？
1.理解一元二次方程的概念，根据 一元二次方程的一般式，确定各项系数；
2.灵活应用一元二次方程概念解决有关问题
3.理解一元二次方程解的概念，并能解决相关问题
学习目标
（1）足球场有多宽
一块足球场的的面积为7140m2，周长为346m，求足球场的长和宽。
(346÷2-x)x=7140
即：-x2+173x-7140=0
一、生活中的数学
解：设足球场的一边为x米，则另一边为 由题意可列：
（346÷2-x)米，
或x2-173x+7140=0
（2）如图，一个直角三角形的三边都是整数，它的斜边长是11cm，两条直角边的差为7cm，求两直角边的长。
做一做

11cm
（X＋7）cm
x2＋(x＋7)2＝112
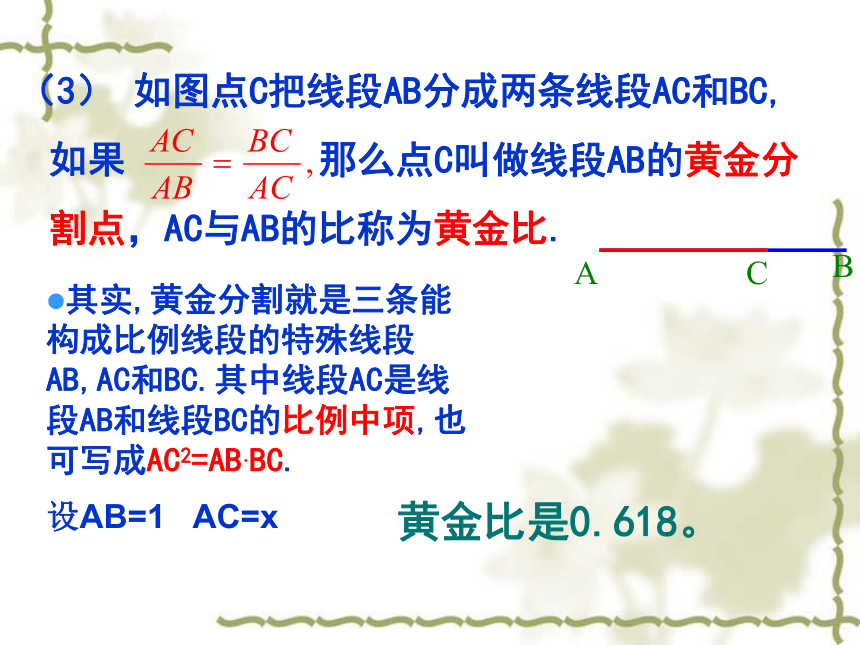
黄金比是0.618。
其实,黄金分割就是三条能构成比例线段的特殊线段AB,AC和BC.其中线段AC是线段AB和线段BC的比例中项,也可写成AC2=AB·BC.
A
B
C
（3） 如图点C把线段AB分成两条线段AC和BC,如果 那么点C叫做线段AB的黄金分割点，AC与AB的比称为黄金比.
设AB=1 AC=x
只含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程.
二、 一元二次方程的概念
三个条件，缺一不可。
（1）一个未知数；
（2）未知数的最高次数是2；
（3）整式方程；
判断条件：
例1、下列方程中哪些是一元二次方程？
（1）
（2）
（3）
（4）
（5）x(5x-2)=x(x+1)+4x2
×
×
×
√
√
例2、下列方程哪些是一元二次方程？
1. 6x2=x
2 . 2x2=5y
3. -x2=0
4.
5. 7x2+6=2x(3x+1)
三、一般形式
ax2＋bx＋c＝0(a、b、c是常数，a≠0)。
ax2叫做二次项，
a叫做二次项系数；
bx叫做一次项，
b叫做一次项系数，
c叫做常数项。
例3、将下列方程化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项：
1）
2）（x-2）(x+3)=8
3）
四、一元二次方程的解：
1、方程解的定义是怎样的呢
能使方程左右两边相等的未知数的值就叫方程的解。只含有一个未知数的方程的解也叫做根。
例4 已知关于x的一元二次方程
(m－1)x2＋3x－5m＋4＝0有一根为2， 求m。
2、随堂练习
1.当m＝ 时，方程x2＋(m＋1)x＋m＋1＝0
　有解x＝0
2.下面哪些数是方程 的根
-4 -3 -2 -1 0 1 2 3 4
3.若方程ax2＋bx＋c＝0的一个解为x=1， a+b+c=
X=-1
X=1
X=2
达标检测：
1、将下列方程化为一般形式，并分别指出它的二次项系数、一次项系数和常数项
2x(x-1)=3(x-5)-4
达标检测：
2.方程（mx－1)x2＋mx＋1=0为关于x的一元二次方程则m 的值为＿＿＿
3.关于x的方程中一定是一元二次方程的是
A. ax2＋bx＋c＝0 B. mx2＋x－m2＝0
C .(m＋1)x2＝(m＋1)2 D.（m2＋1)x2－m2＝0
在什么条件下是一元二次方程？
在什么条件下是一元一次方程？
4.方程（k2－9)x2＋(k－3)x＋3=0
5. 关于x的方程（2m2＋m－3)xm＋1＋5x＝13 可能是一元二次方程吗？
6.若方程kx3－(x－1)2＝3(k－2)x3＋1是关于x的一元二次方程，则k＝＿＿＿
A.1 B.-1 C.1或-1 D.0
（4）当m为何值时,方程
是关于x的一元二次方程.