人教版 九年级上数学 24.1 圆的有关性质 培优课时训练(Word版含答案)
文档属性
| 名称 | 人教版 九年级上数学 24.1 圆的有关性质 培优课时训练(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 597.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 14:22:18 | ||
图片预览




文档简介
人教版
九年级数学
24.1
圆的有关性质
培优课时训练
一、选择题
1.
如图,在⊙O中,若C是的中点,∠A=50°,则∠BOC的度数是( )
A.40°
B.45°
C.50°
D.60°
2.
如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠COE=∠DOE
B.CE=DE
C.OE=BE
D.=
3.
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.
5
B.
7
C.
9
D.
11
4.
在⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM
B.AB=2AM
C.AB<2AM
D.AB与2AM的大小关系不能确定
5.
如图,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1,l2于点B,C,连接AC,BC.若∠ABC=54°,则∠1等于( )
A.36°
B.54°
C.72°
D.73°
6.
如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是( )
A.AP=2OP
B.CD=2OP
C.OB⊥AC
D.AC平分OB
7.
如图,OA是⊙O的半径,B为OA上一点(不与点O,A重合),过点B作OA的垂线交⊙O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8
B.6
C.4
D.2
8.
P为⊙O内一点,若过点P的最长的弦为8
cm,最短的弦为4
cm,则OP的长为( )
A.2
cm
B.
cm
C.3
cm
D.2
cm
9.
如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为( )
A.70°
B.60°
C.50°
D.40°
10.
如图,⊙P与x轴交于点A(—5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+
B.2
+
C.4
D.2
+2
二、填空题
11.
如图,AB为⊙O的直径,CD⊥AB.若AB=10,CD=8,则圆心O到弦CD的距离为________.
12.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
13.
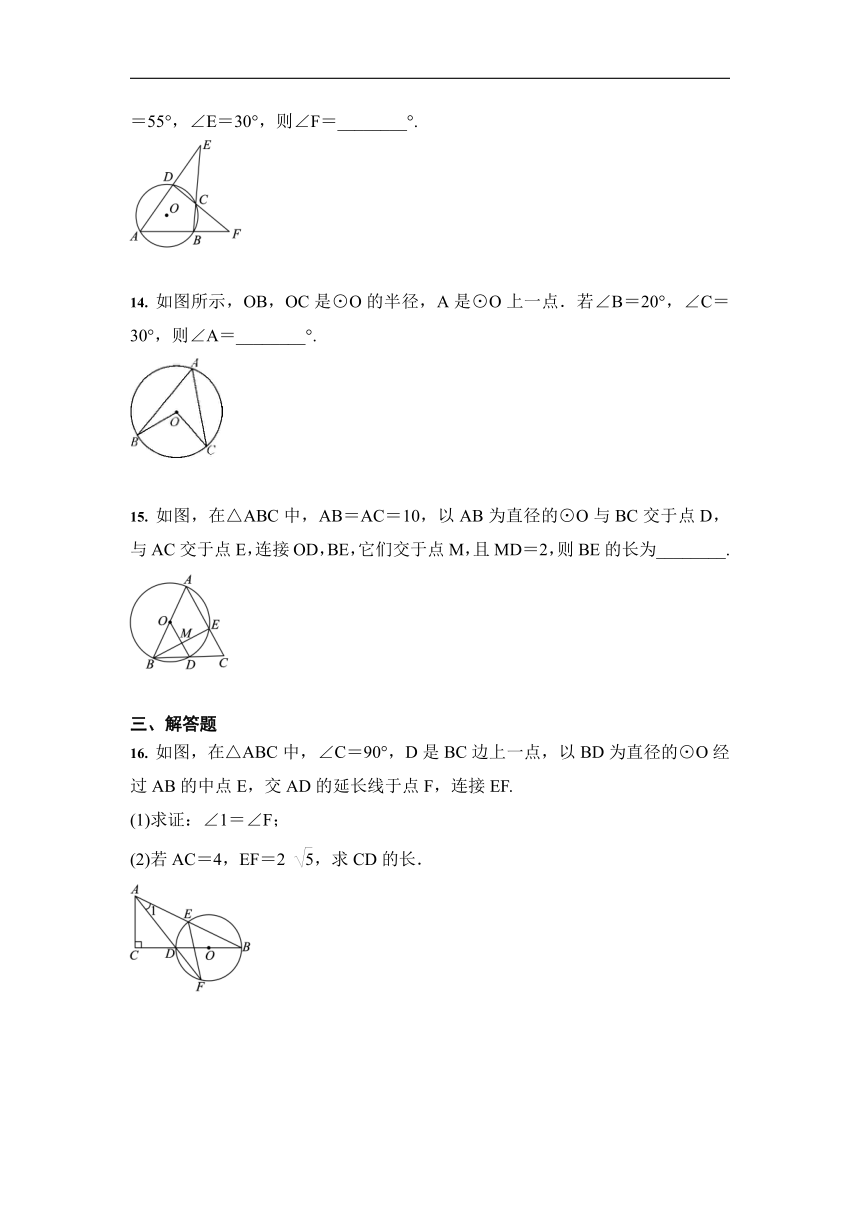
如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=________°.
14.
如图所示,OB,OC是⊙O的半径,A是⊙O上一点.若∠B=20°,∠C=30°,则∠A=________°.
15.
如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连接OD,BE,它们交于点M,且MD=2,则BE的长为________.
三、解答题
16.
如图,在△ABC中,∠C=90°,D是BC边上一点,以BD为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若AC=4,EF=2
,求CD的长.
17.
如图,△ABC和△ABD都是直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.
18.
如图,已知AB是⊙O的直径,C是圆周上的动点,P是优弧ABC的中点.
(1)如图①,求证:OP∥BC;
(2)如图②,PC交AB于点D,当△ODC是等腰三角形时,求∠PAO的度数.
人教版
九年级数学
24.1
圆的有关性质
培优课时训练-答案
一、选择题
1.
【答案】A [解析]
∵∠A=50°,OA=OB,
∴∠B=∠A=50°,
∴∠AOB=180°-50°-50°=80°.
∵C是的中点,
∴∠BOC=∠AOB=40°.
故选A.
2.
【答案】C
3.
【答案】A 【解析】∵ON⊥AB,AB=24,∴AN==12,∴在Rt△AON中,ON===5.
4.
【答案】C [解析]
如图,∵M为的中点,∴AM=BM.
∵AM+BM>AB,
∴AB<2AM.故选C.
5.
【答案】C
6.
【答案】A [解析]
∵AD是⊙O的直径,
∴∠ACD=90°.
∵四边形OBCD是平行四边形,
∴CD∥OB,CD=OB,∴∠CPO=90°,
即OB⊥AC,∴选项C正确;
∴CP=AP.又∵OA=OD,
∴OP是△ACD的中位线,
∴CD=2OP,∴选项B正确;
∴CD=OB=2OP,即P是OB的中点,
∴AC平分OB,∴选项D正确.
7.
【答案】C
8.
【答案】A [解析]
设⊙O中过点P的最长的弦为AB,最短的弦为CD,如图所示,则CD⊥AB于点P.根据题意,得AB=8
cm,CD=4
cm,
∴OC=AB=4
cm.
∵CD⊥AB,
∴CP=CD=2
cm.
在Rt△OCP中,根据勾股定理,得
OP===2
(cm).
9.
【答案】D [解析]
∵∠BOC=110°,∴∠AOC=70°.∵AD∥OC,∴∠A=∠AOC=70°.∵OA=OD,∴∠D=∠A=70°.在△OAD中,∠AOD=180°-(∠A+∠D)=40°.
10.
【答案】B [解析]
如图,连接PA,PB,PC,过点P作PD⊥AB于点D,PE⊥OC于点E.
∵∠ACB=60°,∴∠APB=120°.
∵PA=PB,∴∠PAB=∠PBA=30°.
∵A(-5,0),B(1,0),
∴AB=6,
∴AD=BD=3,
∴PD=,PA=PB=PC=2
.
∵PD⊥AB,PE⊥OC,∠AOC=90°,
∴四边形PEOD是矩形,
∴OE=PD=,PE=OD=3-1=2,
∴CE===2
,
∴OC=CE+OE=2
+,
∴点C的纵坐标为2
+.
故选B.
二、填空题
11.
【答案】3
12.
【答案】215 [解析]
连接CE,则∠B+∠AEC=180°,∠DEC=∠CAD=35°,∴∠B+∠AED=(∠B+∠AEC)+∠DEC=180°+35°=215°.
13.
【答案】40 [解析]
∵∠BCD=180°-∠A=125°,∠CBF=∠A+∠E=85°,∴∠F=∠BCD-∠CBF=125°-85°=40°.
14.
【答案】50 [解析]
连接OA,则OA=OB,OA=OC,
∴∠OAB=∠B,∠OAC=∠C,
∴∠BAC=∠OAB+∠OAC=∠B+∠C=20°+30°=50°.
15.
【答案】8 [解析]
连接AD,如图所示.
∵以AB为直径的⊙O与BC交于点D,与AC交于点E,
∴∠AEB=∠ADB=90°,即AD⊥BC.
又∵AB=AC,
∴BD=CD.
又∵OA=OB,∴OD∥AC,
∴OD⊥BE,∴BM=EM,
∴CE=2MD=4,
∴AE=AC-CE=6,
∴BE===8.
三、解答题
16.
【答案】
解:(1)证明:如图,连接DE.
∵BD是⊙O的直径,
∴∠DEB=90°,即DE⊥AB.
又∵E是AB的中点,
∴AD=BD,∴∠1=∠B.
又∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,∴AE=EF=2
,
∴AB=2AE=4
.
在Rt△ABC中,∵AC=4,∠C=90°,
∴BC==8.
设CD=x,则AD=BD=8-x.
在Rt△ACD中,∵∠C=90°,
∴AC2+CD2=AD2,即42+x2=(8-x)2,
解得x=3,即CD=3.
17.
【答案】
证明:如图,取AB的中点O,连接OC,OD.
∵△ABC和△ABD都是直角三角形,且∠ACB=∠ADB=90°,
∴OC,OD分别为Rt△ABC和Rt△ABD斜边上的中线,
∴OC=OA=OB,OD=OA=OB,
∴OA=OB=OC=OD,
∴A,B,C,D四点在同一个圆上.
18.
【答案】
解:(1)证明:如图①,连接PC.
∵=,∴∠AOP=∠COP.
在△AOP和△COP中,
∴△AOP≌△COP,∴∠APO=∠CPO.
∵OA=OP,∴∠APO=∠OAP.
又∵∠PCB=∠OAP,
∴∠CPO=∠PCB,
∴OP∥BC.
(2)如图②,连接OP,AC.
∵=,∴PA=PC,∴∠PAC=∠PCA.
∵OA=OC,∴∠OAC=∠OCA,
∴∠PAO=∠PCO.
当DO=DC时,设∠DCO=x,
则∠DOC=x,∠PAO=x,
∴∠OPC=∠OCP=x,∠PDO=2x.
∵∠PAO=x,∴∠POD=2∠PAO=2x.
在△POD中,x+2x+2x=180°,解得x=36°,
即∠PAO=36°.
当CO=CD时,设∠DCO=x,
则∠OPC=x,∠PAO=x,
∴∠POD=2x,
∴∠ODC=∠POD+∠OPC=2x+x=3x.
∵CD=CO,
∴∠DOC=∠ODC=3x.
在△POC中,x+x+5x=180°,
解得x=(),即∠PAO=()°,).
当OC=OD时,B,D重合,不符合题意,舍去.
综上所述,∠PAO的度数为36°或()°,).
九年级数学
24.1
圆的有关性质
培优课时训练
一、选择题
1.
如图,在⊙O中,若C是的中点,∠A=50°,则∠BOC的度数是( )
A.40°
B.45°
C.50°
D.60°
2.
如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠COE=∠DOE
B.CE=DE
C.OE=BE
D.=
3.
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.
5
B.
7
C.
9
D.
11
4.
在⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM
B.AB=2AM
C.AB<2AM
D.AB与2AM的大小关系不能确定
5.
如图,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1,l2于点B,C,连接AC,BC.若∠ABC=54°,则∠1等于( )
A.36°
B.54°
C.72°
D.73°
6.
如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是( )
A.AP=2OP
B.CD=2OP
C.OB⊥AC
D.AC平分OB
7.
如图,OA是⊙O的半径,B为OA上一点(不与点O,A重合),过点B作OA的垂线交⊙O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8
B.6
C.4
D.2
8.
P为⊙O内一点,若过点P的最长的弦为8
cm,最短的弦为4
cm,则OP的长为( )
A.2
cm
B.
cm
C.3
cm
D.2
cm
9.
如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为( )
A.70°
B.60°
C.50°
D.40°
10.
如图,⊙P与x轴交于点A(—5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+
B.2
+
C.4
D.2
+2
二、填空题
11.
如图,AB为⊙O的直径,CD⊥AB.若AB=10,CD=8,则圆心O到弦CD的距离为________.
12.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
13.
如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=________°.
14.
如图所示,OB,OC是⊙O的半径,A是⊙O上一点.若∠B=20°,∠C=30°,则∠A=________°.
15.
如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连接OD,BE,它们交于点M,且MD=2,则BE的长为________.
三、解答题
16.
如图,在△ABC中,∠C=90°,D是BC边上一点,以BD为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若AC=4,EF=2
,求CD的长.
17.
如图,△ABC和△ABD都是直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.
18.
如图,已知AB是⊙O的直径,C是圆周上的动点,P是优弧ABC的中点.
(1)如图①,求证:OP∥BC;
(2)如图②,PC交AB于点D,当△ODC是等腰三角形时,求∠PAO的度数.
人教版
九年级数学
24.1
圆的有关性质
培优课时训练-答案
一、选择题
1.
【答案】A [解析]
∵∠A=50°,OA=OB,
∴∠B=∠A=50°,
∴∠AOB=180°-50°-50°=80°.
∵C是的中点,
∴∠BOC=∠AOB=40°.
故选A.
2.
【答案】C
3.
【答案】A 【解析】∵ON⊥AB,AB=24,∴AN==12,∴在Rt△AON中,ON===5.
4.
【答案】C [解析]
如图,∵M为的中点,∴AM=BM.
∵AM+BM>AB,
∴AB<2AM.故选C.
5.
【答案】C
6.
【答案】A [解析]
∵AD是⊙O的直径,
∴∠ACD=90°.
∵四边形OBCD是平行四边形,
∴CD∥OB,CD=OB,∴∠CPO=90°,
即OB⊥AC,∴选项C正确;
∴CP=AP.又∵OA=OD,
∴OP是△ACD的中位线,
∴CD=2OP,∴选项B正确;
∴CD=OB=2OP,即P是OB的中点,
∴AC平分OB,∴选项D正确.
7.
【答案】C
8.
【答案】A [解析]
设⊙O中过点P的最长的弦为AB,最短的弦为CD,如图所示,则CD⊥AB于点P.根据题意,得AB=8
cm,CD=4
cm,
∴OC=AB=4
cm.
∵CD⊥AB,
∴CP=CD=2
cm.
在Rt△OCP中,根据勾股定理,得
OP===2
(cm).
9.
【答案】D [解析]
∵∠BOC=110°,∴∠AOC=70°.∵AD∥OC,∴∠A=∠AOC=70°.∵OA=OD,∴∠D=∠A=70°.在△OAD中,∠AOD=180°-(∠A+∠D)=40°.
10.
【答案】B [解析]
如图,连接PA,PB,PC,过点P作PD⊥AB于点D,PE⊥OC于点E.
∵∠ACB=60°,∴∠APB=120°.
∵PA=PB,∴∠PAB=∠PBA=30°.
∵A(-5,0),B(1,0),
∴AB=6,
∴AD=BD=3,
∴PD=,PA=PB=PC=2
.
∵PD⊥AB,PE⊥OC,∠AOC=90°,
∴四边形PEOD是矩形,
∴OE=PD=,PE=OD=3-1=2,
∴CE===2
,
∴OC=CE+OE=2
+,
∴点C的纵坐标为2
+.
故选B.
二、填空题
11.
【答案】3
12.
【答案】215 [解析]
连接CE,则∠B+∠AEC=180°,∠DEC=∠CAD=35°,∴∠B+∠AED=(∠B+∠AEC)+∠DEC=180°+35°=215°.
13.
【答案】40 [解析]
∵∠BCD=180°-∠A=125°,∠CBF=∠A+∠E=85°,∴∠F=∠BCD-∠CBF=125°-85°=40°.
14.
【答案】50 [解析]
连接OA,则OA=OB,OA=OC,
∴∠OAB=∠B,∠OAC=∠C,
∴∠BAC=∠OAB+∠OAC=∠B+∠C=20°+30°=50°.
15.
【答案】8 [解析]
连接AD,如图所示.
∵以AB为直径的⊙O与BC交于点D,与AC交于点E,
∴∠AEB=∠ADB=90°,即AD⊥BC.
又∵AB=AC,
∴BD=CD.
又∵OA=OB,∴OD∥AC,
∴OD⊥BE,∴BM=EM,
∴CE=2MD=4,
∴AE=AC-CE=6,
∴BE===8.
三、解答题
16.
【答案】
解:(1)证明:如图,连接DE.
∵BD是⊙O的直径,
∴∠DEB=90°,即DE⊥AB.
又∵E是AB的中点,
∴AD=BD,∴∠1=∠B.
又∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,∴AE=EF=2
,
∴AB=2AE=4
.
在Rt△ABC中,∵AC=4,∠C=90°,
∴BC==8.
设CD=x,则AD=BD=8-x.
在Rt△ACD中,∵∠C=90°,
∴AC2+CD2=AD2,即42+x2=(8-x)2,
解得x=3,即CD=3.
17.
【答案】
证明:如图,取AB的中点O,连接OC,OD.
∵△ABC和△ABD都是直角三角形,且∠ACB=∠ADB=90°,
∴OC,OD分别为Rt△ABC和Rt△ABD斜边上的中线,
∴OC=OA=OB,OD=OA=OB,
∴OA=OB=OC=OD,
∴A,B,C,D四点在同一个圆上.
18.
【答案】
解:(1)证明:如图①,连接PC.
∵=,∴∠AOP=∠COP.
在△AOP和△COP中,
∴△AOP≌△COP,∴∠APO=∠CPO.
∵OA=OP,∴∠APO=∠OAP.
又∵∠PCB=∠OAP,
∴∠CPO=∠PCB,
∴OP∥BC.
(2)如图②,连接OP,AC.
∵=,∴PA=PC,∴∠PAC=∠PCA.
∵OA=OC,∴∠OAC=∠OCA,
∴∠PAO=∠PCO.
当DO=DC时,设∠DCO=x,
则∠DOC=x,∠PAO=x,
∴∠OPC=∠OCP=x,∠PDO=2x.
∵∠PAO=x,∴∠POD=2∠PAO=2x.
在△POD中,x+2x+2x=180°,解得x=36°,
即∠PAO=36°.
当CO=CD时,设∠DCO=x,
则∠OPC=x,∠PAO=x,
∴∠POD=2x,
∴∠ODC=∠POD+∠OPC=2x+x=3x.
∵CD=CO,
∴∠DOC=∠ODC=3x.
在△POC中,x+x+5x=180°,
解得x=(),即∠PAO=()°,).
当OC=OD时,B,D重合,不符合题意,舍去.
综上所述,∠PAO的度数为36°或()°,).
同课章节目录
