小学数学五年级上册数学教案-5.1 平行四边形 沪教版 (word版)
文档属性
| 名称 | 小学数学五年级上册数学教案-5.1 平行四边形 沪教版 (word版) |  | |
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 13:25:36 | ||
图片预览

文档简介
平行四边形的面积
学习目标:
经历平行四边形转化成长方形的过程,探索平行四边形面积公式。
掌握平行四边形面积的计算公式,能用规范的书写格式正确计算。
初步学会用思维工具解决问题。
重点:掌握平行四边形的计算公式。
难点:初步学会用思维工具解决问题。
学具:平行四边形、方格纸、尺、剪刀、活动平行四边形框架
教学过程:
预学单:1、看书P64例1,初步理解平行四边形的面积公式。
尝试完成P65题1、2。
一、引领探究
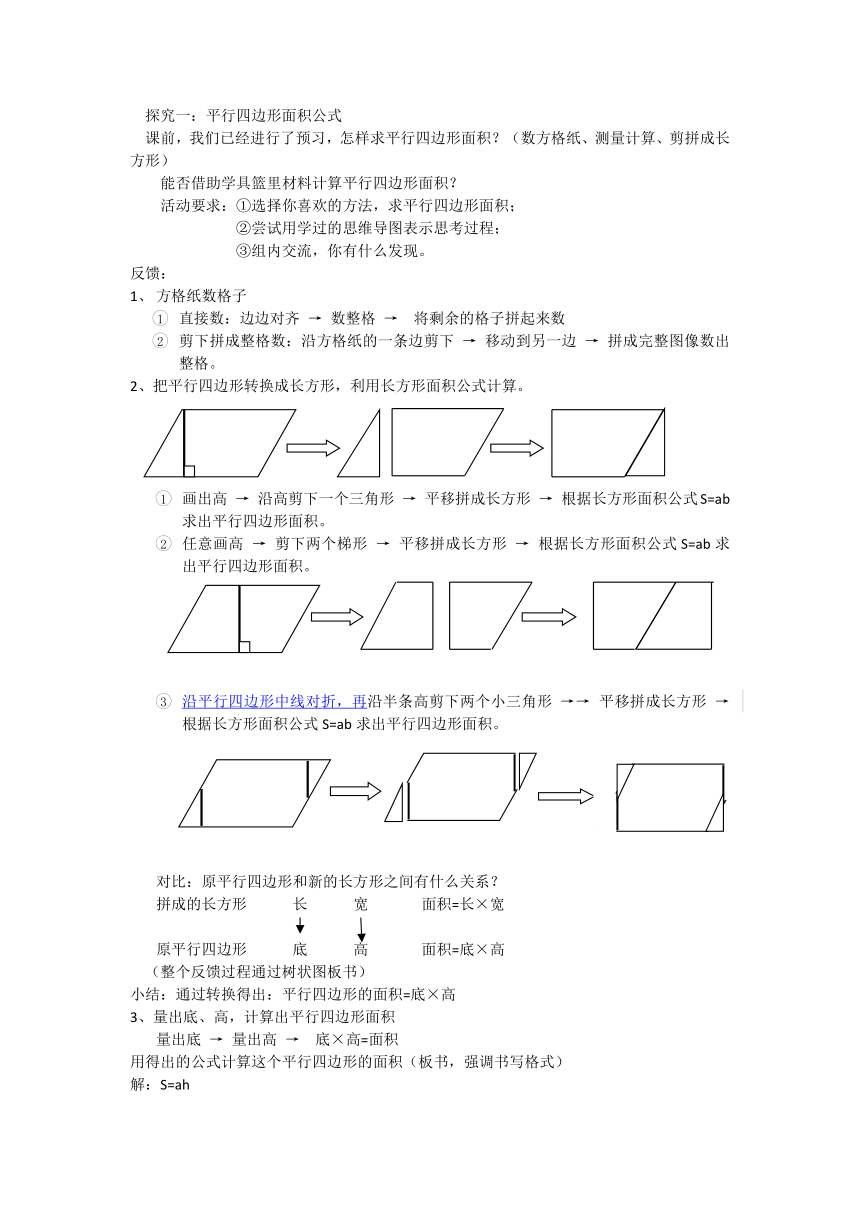
出示平行四边形:昨天,我们已经认识了平行四边形,借助单气泡图,说说平行四边形有哪些特征。
2、通过双气泡图比较平行四边形和长方形的异同。
3、揭题-----今天我们继续探究平行四边形的面积。
二、自主探究
探究一:平行四边形面积公式
课前,我们已经进行了预习,怎样求平行四边形面积?(数方格纸、测量计算、剪拼成长方形)
能否借助学具篮里材料计算平行四边形面积?
活动要求:①选择你喜欢的方法,求平行四边形面积;
②尝试用学过的思维导图表示思考过程;
③组内交流,你有什么发现。
反馈:
方格纸数格子
直接数:边边对齐 → 数整格 → 将剩余的格子拼起来数
剪下拼成整格数:沿方格纸的一条边剪下 → 移动到另一边 → 拼成完整图像数出整格。
2、把平行四边形转换成长方形,利用长方形面积公式计算。
画出高 → 沿高剪下一个三角形 → 平移拼成长方形 → 根据长方形面积公式S=ab求出平行四边形面积。
任意画高 → 剪下两个梯形 → 平移拼成长方形 → 根据长方形面积公式S=ab求出平行四边形面积。
沿平行四边形中线对折,再沿半条高剪下两个小三角形 →→ 平移拼成长方形 → 根据长方形面积公式S=ab求出平行四边形面积。
对比:原平行四边形和新的长方形之间有什么关系?
拼成的长方形 长 宽 面积=长×宽
原平行四边形 底 高 面积=底×高
(整个反馈过程通过树状图板书)
小结:通过转换得出:平行四边形的面积=底×高
3、量出底、高,计算出平行四边形面积
量出底 → 量出高 → 底×高=面积
用得出的公式计算这个平行四边形的面积(板书,强调书写格式)
解:S=ah
=4×6
=24(cm?)
答:这个平行四边形的面积是24 cm?。
反馈预学单练习:① 4×6=24cm? ② 3×3=9㎡(对应底高) ③不能求
三、感悟探究
1、基础练习:
2、选择题
1)一个平行四边形的面积是5.6平方米,高是2.8平方米,这条高对应的底是( )厘米。
A.2 B.20 C.200 D.0.2
桥型图复习单位进率:
2)把一个长方形框架拉成一个平行四边形,原来长方形与平行四边形相比( )
A.周长相等,面积不等 B.周长不等,面积相等
C.周长和面积都相等 D.周长和面积都不相等
3) 下图是一块平行四边形菜地,如果要用篱笆把菜地围起来,需要( )米长篱笆;如果每平方米能收10.4千克青菜,这块地一共能收( )千克青菜。
A.(4+6)×2=20 B.5×6×10.4=312
C.4×6×10.4=249.6 D.(5+6)×2=22
3、拓展题:
比较下图中甲乙两个阴影部分面积的大小:甲( )乙
甲 乙
板书设计:平行四边形的面积
平行四边形面积=底×高
长方形面积=长×宽
学习目标:
经历平行四边形转化成长方形的过程,探索平行四边形面积公式。
掌握平行四边形面积的计算公式,能用规范的书写格式正确计算。
初步学会用思维工具解决问题。
重点:掌握平行四边形的计算公式。
难点:初步学会用思维工具解决问题。
学具:平行四边形、方格纸、尺、剪刀、活动平行四边形框架
教学过程:
预学单:1、看书P64例1,初步理解平行四边形的面积公式。
尝试完成P65题1、2。
一、引领探究
出示平行四边形:昨天,我们已经认识了平行四边形,借助单气泡图,说说平行四边形有哪些特征。
2、通过双气泡图比较平行四边形和长方形的异同。
3、揭题-----今天我们继续探究平行四边形的面积。
二、自主探究
探究一:平行四边形面积公式
课前,我们已经进行了预习,怎样求平行四边形面积?(数方格纸、测量计算、剪拼成长方形)
能否借助学具篮里材料计算平行四边形面积?
活动要求:①选择你喜欢的方法,求平行四边形面积;
②尝试用学过的思维导图表示思考过程;
③组内交流,你有什么发现。
反馈:
方格纸数格子
直接数:边边对齐 → 数整格 → 将剩余的格子拼起来数
剪下拼成整格数:沿方格纸的一条边剪下 → 移动到另一边 → 拼成完整图像数出整格。
2、把平行四边形转换成长方形,利用长方形面积公式计算。
画出高 → 沿高剪下一个三角形 → 平移拼成长方形 → 根据长方形面积公式S=ab求出平行四边形面积。
任意画高 → 剪下两个梯形 → 平移拼成长方形 → 根据长方形面积公式S=ab求出平行四边形面积。
沿平行四边形中线对折,再沿半条高剪下两个小三角形 →→ 平移拼成长方形 → 根据长方形面积公式S=ab求出平行四边形面积。
对比:原平行四边形和新的长方形之间有什么关系?
拼成的长方形 长 宽 面积=长×宽
原平行四边形 底 高 面积=底×高
(整个反馈过程通过树状图板书)
小结:通过转换得出:平行四边形的面积=底×高
3、量出底、高,计算出平行四边形面积
量出底 → 量出高 → 底×高=面积
用得出的公式计算这个平行四边形的面积(板书,强调书写格式)
解:S=ah
=4×6
=24(cm?)
答:这个平行四边形的面积是24 cm?。
反馈预学单练习:① 4×6=24cm? ② 3×3=9㎡(对应底高) ③不能求
三、感悟探究
1、基础练习:
2、选择题
1)一个平行四边形的面积是5.6平方米,高是2.8平方米,这条高对应的底是( )厘米。
A.2 B.20 C.200 D.0.2
桥型图复习单位进率:
2)把一个长方形框架拉成一个平行四边形,原来长方形与平行四边形相比( )
A.周长相等,面积不等 B.周长不等,面积相等
C.周长和面积都相等 D.周长和面积都不相等
3) 下图是一块平行四边形菜地,如果要用篱笆把菜地围起来,需要( )米长篱笆;如果每平方米能收10.4千克青菜,这块地一共能收( )千克青菜。
A.(4+6)×2=20 B.5×6×10.4=312
C.4×6×10.4=249.6 D.(5+6)×2=22
3、拓展题:
比较下图中甲乙两个阴影部分面积的大小:甲( )乙
甲 乙
板书设计:平行四边形的面积
平行四边形面积=底×高
长方形面积=长×宽
同课章节目录
