13.1实数(1)
图片预览








文档简介
(共27张PPT)
2.使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
1.你还记得什么叫有理数吗?
学习目标
1. 了解无理数和实数的概念, 能对实数按要求分类;
2. 知道实数与数轴上的点具有 一一对应关系。
自学指导
自学课本P82-83页内容,完成下列思考题
(1)观察下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗?
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕
有理数和无理数统称实数.
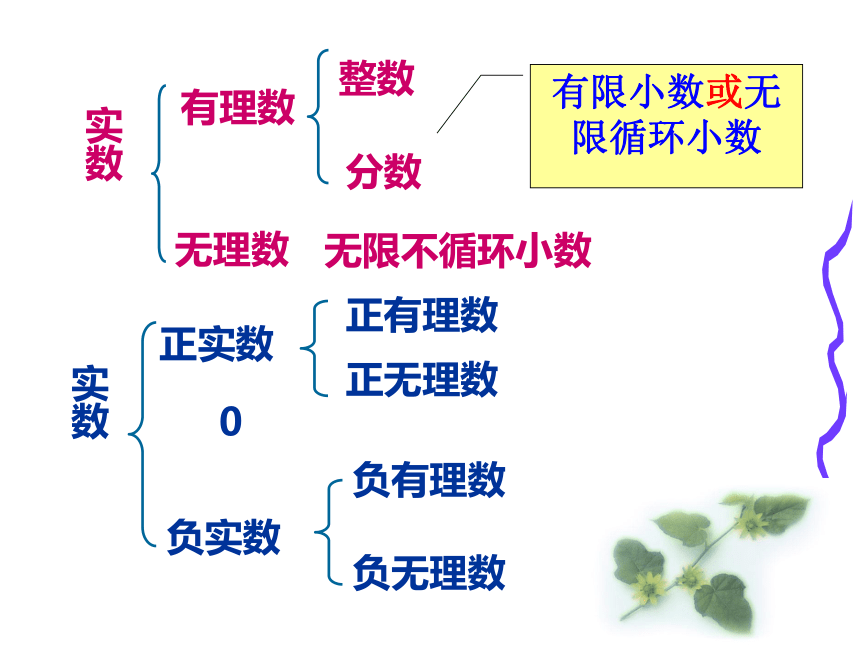
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
例1:把下列各数分别填入相应的集合内:
有理数集合
无理数集合
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
练一练:把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗
0
1
2
3
-1
-2
-3
4
-4
﹒
O’
能在数轴上找到表示π的点吗
0
1
2
4
3
-1
-2
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
你能把 在数轴上表示出来吗?请与同桌一起试一试。
有理数能不能将数轴排满?
0
1
2
3
-1
-2
-3
4
-4
实数与数轴上的点是一一对应的.
同样的,平面直角坐标系中的点与有序实数对是一一对应的.
0
1
2
3
-1
-2
-3
4
-4
学以致用
1.如图,数轴上点P表示的数可能是( )
A B C D
0
-2
4
-1
1
2
3
-3
P
-3.2
2.如下图,数轴上表示 的点是______
3.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数可能是_____
0
-2
4
-1
1
2
3
5
A
B
C
B
B
A
探究新知
问题:
思考 互为相反数的定义及性质
绝对值的定义及性质
猜测:
的相反数是_____
-π的相反数是_____
0的相反数是_____
=_______, ︱ -π ︱=_______, ︱ 0︱=______
π
0
π
0
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
(1)a是一个实数,它的相反数为 ,
绝对值为 ;
(2)如果a 0,那么它的倒数为 .
(1)分别写出- , 的相反数;
(2)指出
(3)求
(4)已知一个数的绝对值是
求这个数.
例2:
填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平 方 是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
5、一个数的绝对值是 ,则这个数是 .
练习:
一.求下列各数的相反数和绝对值:
课堂检测
二、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
√
×
√
×
×
×
整数有 有理数有
无理数有 实数有
课堂检测
三、填空
在实数
中,
这节课你有什么新发现?知道了哪些新知识?
2.使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
1.你还记得什么叫有理数吗?
学习目标
1. 了解无理数和实数的概念, 能对实数按要求分类;
2. 知道实数与数轴上的点具有 一一对应关系。
自学指导
自学课本P82-83页内容,完成下列思考题
(1)观察下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗?
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕
有理数和无理数统称实数.
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
例1:把下列各数分别填入相应的集合内:
有理数集合
无理数集合
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
练一练:把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗
0
1
2
3
-1
-2
-3
4
-4
﹒
O’
能在数轴上找到表示π的点吗
0
1
2
4
3
-1
-2
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
你能把 在数轴上表示出来吗?请与同桌一起试一试。
有理数能不能将数轴排满?
0
1
2
3
-1
-2
-3
4
-4
实数与数轴上的点是一一对应的.
同样的,平面直角坐标系中的点与有序实数对是一一对应的.
0
1
2
3
-1
-2
-3
4
-4
学以致用
1.如图,数轴上点P表示的数可能是( )
A B C D
0
-2
4
-1
1
2
3
-3
P
-3.2
2.如下图,数轴上表示 的点是______
3.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数可能是_____
0
-2
4
-1
1
2
3
5
A
B
C
B
B
A
探究新知
问题:
思考 互为相反数的定义及性质
绝对值的定义及性质
猜测:
的相反数是_____
-π的相反数是_____
0的相反数是_____
=_______, ︱ -π ︱=_______, ︱ 0︱=______
π
0
π
0
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
(1)a是一个实数,它的相反数为 ,
绝对值为 ;
(2)如果a 0,那么它的倒数为 .
(1)分别写出- , 的相反数;
(2)指出
(3)求
(4)已知一个数的绝对值是
求这个数.
例2:
填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平 方 是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
5、一个数的绝对值是 ,则这个数是 .
练习:
一.求下列各数的相反数和绝对值:
课堂检测
二、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
√
×
√
×
×
×
整数有 有理数有
无理数有 实数有
课堂检测
三、填空
在实数
中,
这节课你有什么新发现?知道了哪些新知识?
