抛物线的标准方程
图片预览

文档简介
抛物线的标准方程(共2课时)
目标:掌握抛物线的定义和标准方程的几种形式,会画抛物线的草图会;处理简单的直线与抛物线的位置关系问题。
重点:抛物线的标准方程和定义的应用。
难点:抛物线标准方程的各种形式。
一、课前预习
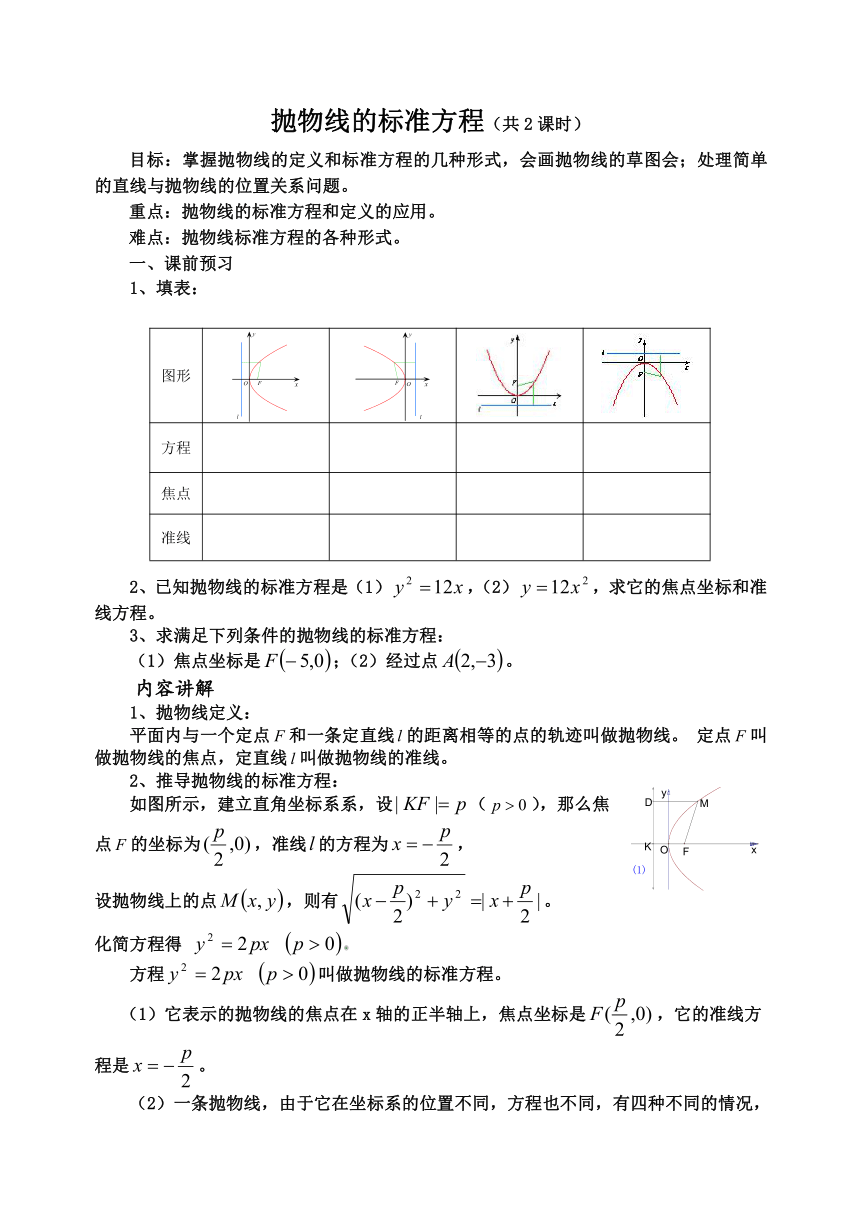
图形
方程
焦点
准线
1、填表:
2、已知抛物线的标准方程是(1),(2),求它的焦点坐标和准线方程。
3、求满足下列条件的抛物线的标准方程:
(1)焦点坐标是;(2)经过点。
内容讲解
1、抛物线定义:
平面内与一个定点和一条定直线的距离相等的点的轨迹叫做抛物线。 定点叫做抛物线的焦点,定直线叫做抛物线的准线。
2、推导抛物线的标准方程:
如图所示,建立直角坐标系系,设(),那么焦点的坐标为,准线的方程为,
设抛物线上的点,则有。
化简方程得
方程叫做抛物线的标准方程。
(1)它表示的抛物线的焦点在x轴的正半轴上,焦点坐标是,它的准线方程是。
(2)一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式:,,.这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下。
3、抛物线的准线方程:如图所示,分别建立直角坐标系,设出(),则抛物线的标准方程如下:
(1), 焦点:,准线:。
(2), 焦点:,准线:。
(3), 焦点:,准线:。
(4) , 焦点:,准线:。
相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂直,垂足与焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的,即。
不同点:(1)图形关于轴对称时,为一次项,为二次项,方程右端为、左端为;图形关于轴对称时,为二次项,为一次项,方程右端为,左端为。 (2)开口方向在轴(或轴)正向时,焦点在轴(或轴)的正半轴上,方程右端取正号;开口在轴(或轴)负向时,焦点在轴(或轴)负半轴时,方程右端取负号。
焦点在轴上的抛物线标准方程:。
焦点在轴上的抛物线标准方程:。
4、抛物线的焦半径及其应用:
定义:抛物线上任意一点与抛物线焦点的连线段,叫做抛物线的焦半径。
焦半径公式:
抛物线,;
抛物线, ;
抛物线, ;
抛物线,。
5、焦点弦:
定义:过焦点的直线割抛物线所成的相交弦。
焦点弦公式:设两交点,可以通过两次焦半径公式得到:
当抛物线焦点在轴上时,焦点弦只和两焦点的横坐标有关:
抛物线, 。
抛物线, 。
当抛物线焦点在轴上时,焦点弦只和两焦点的纵坐标有关:
抛物线, 。
抛物线,。
6、通径
定义:过焦点且垂直于对称轴的相交弦。
直接应用抛物线定义,得到通径:。
7、几个常见的结论:
已知抛物线,若过焦点的直线倾斜角,与抛物线两交于点,两交点,则
(1);(2),;
(3)。
二、例题讲解
例1、(1)已知抛物线标准方程是,求它的焦点坐标和准线方程。
(2)已知抛物线的焦点坐标是,求它的标准方程。
变式训练:1、根据下列条件写出抛物线的标准方程
(1)焦点;(2)准线方程;(3)焦点到准线的距离为
2、求下列抛物线的焦点坐标和准线方程
(1);(2);(3);(4)
例2、已知抛物线的顶点在原点,对称轴为轴,抛物线上的点到焦点的距离等于,求抛物线的方程和的值。
变式训练:1、抛物线()上一点到焦点距离是(),则点到准线的距离是_______,点的横坐标是__________。
2、若点A(3,2)在抛物线y2=2x内,焦点为F,点P在抛物线上移动,当取最小值时,点的坐标是_________,这个最小值是________。
例3、已知抛物线与定点,过点作直线交抛物线于、两点,求线段中点的轨迹方程。
变式训练:设抛物线过定点,且以直线为准线。求抛物线顶点的轨迹的方程。
例4、斜率为的直线经过抛物线的焦点,与抛物线相交于两点、,求线段的长。
变式训练:求过定点且与抛物线只有一个公共点直线方程。
随堂练习
1、抛物线的顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上,此抛物线的方程是 ( )
A、 B、 C、 D、
2翰3333、过点(0,1)且与抛物线只有一个公共点的直线有 ( )
A、一条 B、两条 C、三条 D、无数条
3、过抛物线的焦点作倾斜角为的直线交抛物线于A、B两点,则AB的长是 ( )
A、 B、4 C、8 D、2
4、已知抛物线的焦点为,准线与轴的交点为,点在上且,则的面积为( )
A、 B、 C、 D、
5、点与点的距离比它到直线的距离小1,则点的轨迹方程是_____________。
6、经过点(2,0)斜率为1的直线与抛物线相交与点A、B,求线段AB的长。
目标:掌握抛物线的定义和标准方程的几种形式,会画抛物线的草图会;处理简单的直线与抛物线的位置关系问题。
重点:抛物线的标准方程和定义的应用。
难点:抛物线标准方程的各种形式。
一、课前预习
图形
方程
焦点
准线
1、填表:
2、已知抛物线的标准方程是(1),(2),求它的焦点坐标和准线方程。
3、求满足下列条件的抛物线的标准方程:
(1)焦点坐标是;(2)经过点。
内容讲解
1、抛物线定义:
平面内与一个定点和一条定直线的距离相等的点的轨迹叫做抛物线。 定点叫做抛物线的焦点,定直线叫做抛物线的准线。
2、推导抛物线的标准方程:
如图所示,建立直角坐标系系,设(),那么焦点的坐标为,准线的方程为,
设抛物线上的点,则有。
化简方程得
方程叫做抛物线的标准方程。
(1)它表示的抛物线的焦点在x轴的正半轴上,焦点坐标是,它的准线方程是。
(2)一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式:,,.这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下。
3、抛物线的准线方程:如图所示,分别建立直角坐标系,设出(),则抛物线的标准方程如下:
(1), 焦点:,准线:。
(2), 焦点:,准线:。
(3), 焦点:,准线:。
(4) , 焦点:,准线:。
相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂直,垂足与焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的,即。
不同点:(1)图形关于轴对称时,为一次项,为二次项,方程右端为、左端为;图形关于轴对称时,为二次项,为一次项,方程右端为,左端为。 (2)开口方向在轴(或轴)正向时,焦点在轴(或轴)的正半轴上,方程右端取正号;开口在轴(或轴)负向时,焦点在轴(或轴)负半轴时,方程右端取负号。
焦点在轴上的抛物线标准方程:。
焦点在轴上的抛物线标准方程:。
4、抛物线的焦半径及其应用:
定义:抛物线上任意一点与抛物线焦点的连线段,叫做抛物线的焦半径。
焦半径公式:
抛物线,;
抛物线, ;
抛物线, ;
抛物线,。
5、焦点弦:
定义:过焦点的直线割抛物线所成的相交弦。
焦点弦公式:设两交点,可以通过两次焦半径公式得到:
当抛物线焦点在轴上时,焦点弦只和两焦点的横坐标有关:
抛物线, 。
抛物线, 。
当抛物线焦点在轴上时,焦点弦只和两焦点的纵坐标有关:
抛物线, 。
抛物线,。
6、通径
定义:过焦点且垂直于对称轴的相交弦。
直接应用抛物线定义,得到通径:。
7、几个常见的结论:
已知抛物线,若过焦点的直线倾斜角,与抛物线两交于点,两交点,则
(1);(2),;
(3)。
二、例题讲解
例1、(1)已知抛物线标准方程是,求它的焦点坐标和准线方程。
(2)已知抛物线的焦点坐标是,求它的标准方程。
变式训练:1、根据下列条件写出抛物线的标准方程
(1)焦点;(2)准线方程;(3)焦点到准线的距离为
2、求下列抛物线的焦点坐标和准线方程
(1);(2);(3);(4)
例2、已知抛物线的顶点在原点,对称轴为轴,抛物线上的点到焦点的距离等于,求抛物线的方程和的值。
变式训练:1、抛物线()上一点到焦点距离是(),则点到准线的距离是_______,点的横坐标是__________。
2、若点A(3,2)在抛物线y2=2x内,焦点为F,点P在抛物线上移动,当取最小值时,点的坐标是_________,这个最小值是________。
例3、已知抛物线与定点,过点作直线交抛物线于、两点,求线段中点的轨迹方程。
变式训练:设抛物线过定点,且以直线为准线。求抛物线顶点的轨迹的方程。
例4、斜率为的直线经过抛物线的焦点,与抛物线相交于两点、,求线段的长。
变式训练:求过定点且与抛物线只有一个公共点直线方程。
随堂练习
1、抛物线的顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上,此抛物线的方程是 ( )
A、 B、 C、 D、
2翰3333、过点(0,1)且与抛物线只有一个公共点的直线有 ( )
A、一条 B、两条 C、三条 D、无数条
3、过抛物线的焦点作倾斜角为的直线交抛物线于A、B两点,则AB的长是 ( )
A、 B、4 C、8 D、2
4、已知抛物线的焦点为,准线与轴的交点为,点在上且,则的面积为( )
A、 B、 C、 D、
5、点与点的距离比它到直线的距离小1,则点的轨迹方程是_____________。
6、经过点(2,0)斜率为1的直线与抛物线相交与点A、B,求线段AB的长。
