1.5.1 三角函数的应用 同步练习(含解析)
文档属性
| 名称 | 1.5.1 三角函数的应用 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版初中数学九年级下册第1章直角三角形的边角关系
1.5 三角函数的应用同步练习(一)
一.选择题
1.如图所示,河堤横断面迎水坡的坡比是,堤高,则迎水坡宽度的长为
A. B. C. D.
2.如图,某停车场入口的栏杆,从水平位置绕点旋转到的位置,已知的长为3米.若栏杆的旋转,则栏杆端升高的高度为
A.米 B.米 C.米 D.米
3.如图,滑动调节式遮阳伞的立柱垂直于地面,为立柱上的滑动调节点,伞体的截面示意图为,为的中点,,,,.根据生活经验,当太阳光线与垂直时,遮阳效果最佳,在上午时,太阳光线与地面的夹角为,若要遮阳效果最佳的长约为
(参考数据:,,,
A. B. C. D.
4.如图,一块直角三角板和一张光盘竖放在桌面上,其中是光盘与桌面的切点,,光盘的直径是,则斜边被光盘截得的线段长为
A. B. C. D.
5.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表,如图是一个根据长春的地理位置设计的圭表,其中,立柱的高为,已知冬至时长春的正午光入射角约为,则立柱根部与圭表的冬至线的距离(距的长)约为
A. B. C. D.
6.如图,将宽为的纸条沿折叠,使,则折叠后重叠部分的面积为
A. B. C. D.
二.填空题
7.如图,一人乘雪橇沿坡比的斜坡笔直滑下72米,那么他下降的高度为 米.
8.如图,某商店营业大厅自动扶梯的倾斜角为,的长为12米,则大厅两层之间的高度为 米.(结果保留一位小数)【参考数据:,,】
9.如图是一斜坡的横截面,某人沿着坡度为的斜坡从点向上走了5米到点处,则此时人离水平面的垂直高度为 .
10.如图,校园内有一棵与地面垂直的树,树高为米,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成角时,第二次是阳光与地面成角时,则两次测量的影长差为 米.
11.港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术而闻名世界.其主体工程青州航道桥是一座双塔双索面钢箱梁斜拉桥,两座索塔及索塔两侧的斜拉索对称分布,塔高为163米,大桥主跨的中点为,记斜拉索与大桥主梁所夹锐角为,那么用塔高和的三角函数表示主跨的长为 米.
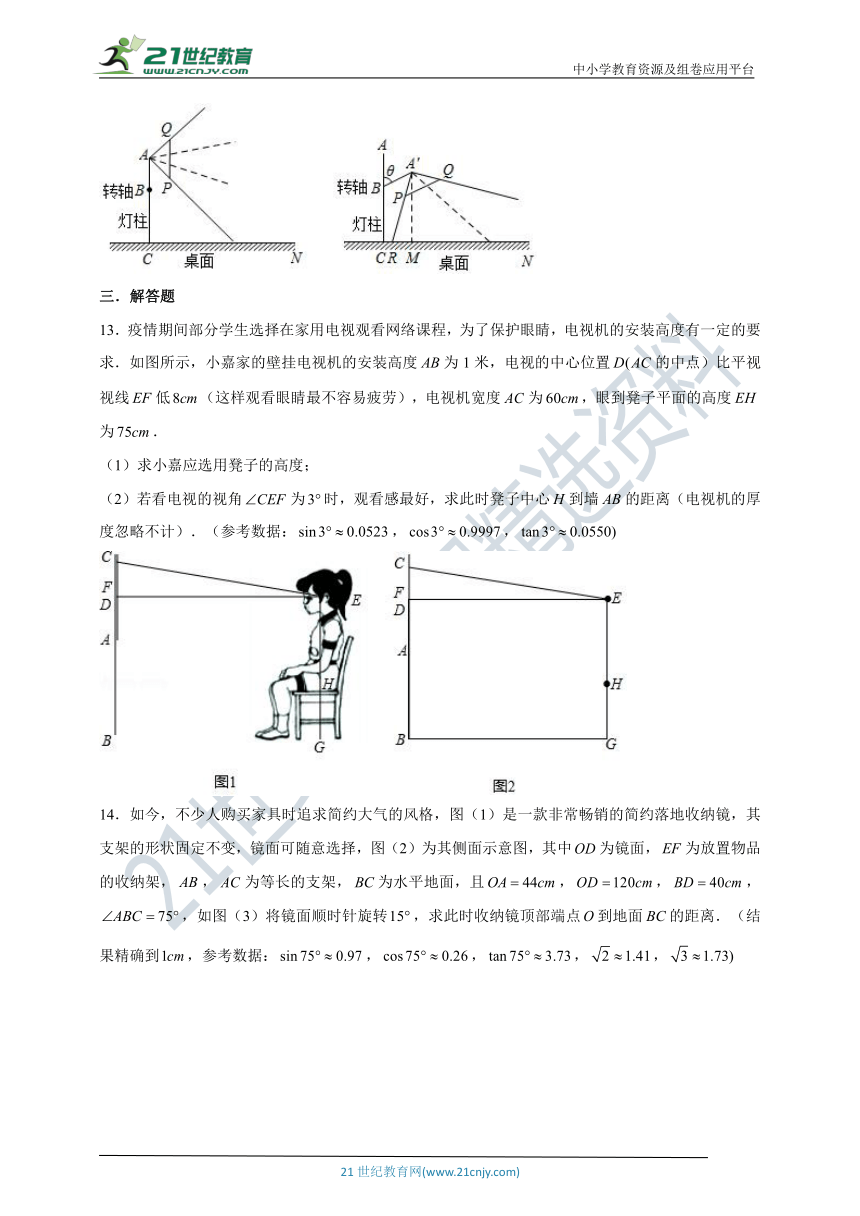
12.如图是某种台灯的示意图,可弯曲,根据测量,灯罩的截面是等腰直角三角形,此时很大一部分光照向远方而没有射在桌面上,若使绕转轴顺时针转动,可使台灯的光更多地落在桌面上.如图,现测得,且,灯心到桌面的距离,则此时 .若继续转动使与灯柱垂直,则此时台灯照在桌面上的最大面积为 .
三.解答题
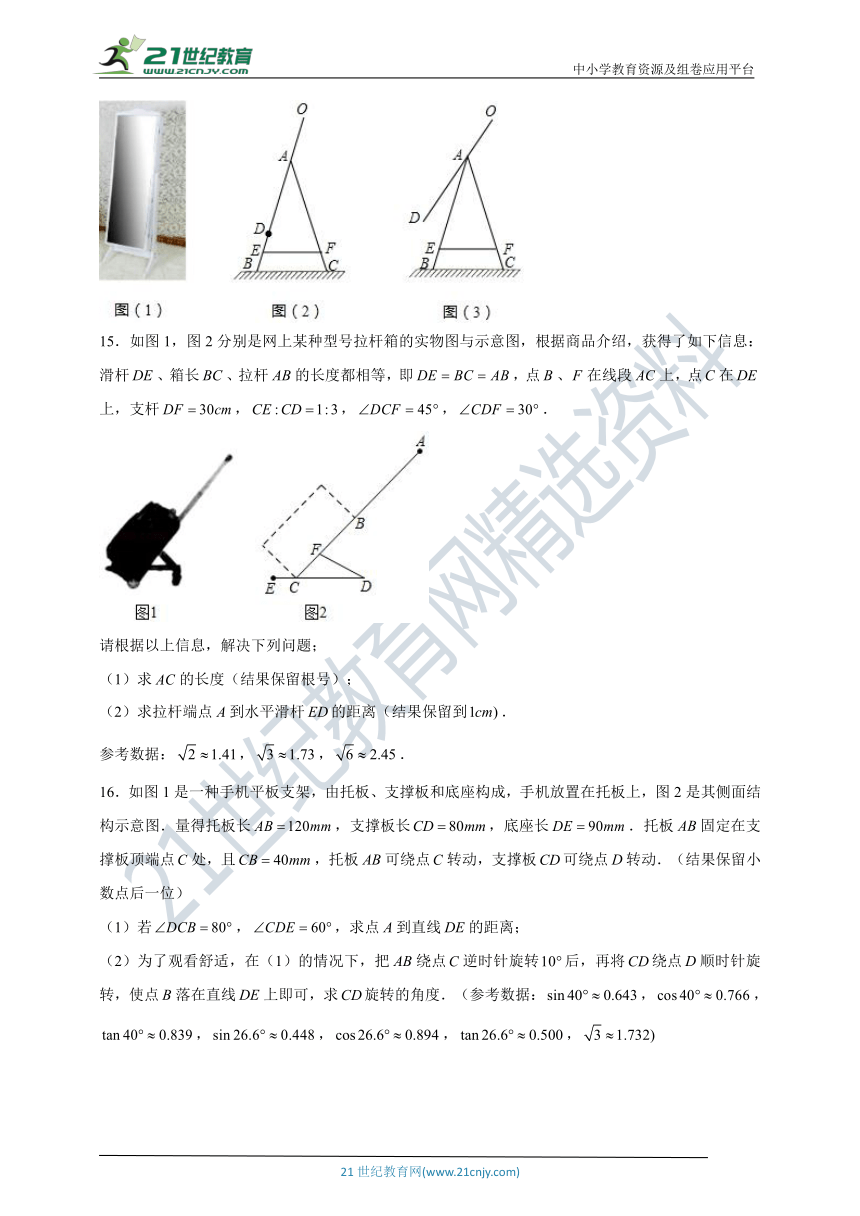
13.疫情期间部分学生选择在家用电视观看网络课程,为了保护眼睛,电视机的安装高度有一定的要求.如图所示,小嘉家的壁挂电视机的安装高度为1米,电视的中心位置的中点)比平视视线低(这样观看眼睛最不容易疲劳),电视机宽度为,眼到凳子平面的高度为.
(1)求小嘉应选用凳子的高度;
(2)若看电视的视角为时,观看感最好,求此时凳子中心到墙的距离(电视机的厚度忽略不计).(参考数据:,,
14.如今,不少人购买家具时追求简约大气的风格,图(1)是一款非常畅销的简约落地收纳镜,其支架的形状固定不变,镜面可随意选择,图(2)为其侧面示意图,其中为镜面,为放置物品的收纳架,,为等长的支架,为水平地面,且,,,,如图(3)将镜面顺时针旋转,求此时收纳镜顶部端点到地面的距离.(结果精确到,参考数据:,,,,
15.如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆、箱长、拉杆的长度都相等,即,点、在线段上,点在上,支杆,,,.
请根据以上信息,解决下列问题;
(1)求的长度(结果保留根号);
(2)求拉杆端点到水平滑杆的距离(结果保留到.
参考数据:,,.
16.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.量得托板长,支撑板长,底座长.托板固定在支撑板顶端点处,且,托板可绕点转动,支撑板可绕点转动.(结果保留小数点后一位)
(1)若,,求点到直线的距离;
(2)为了观看舒适,在(1)的情况下,把绕点逆时针旋转后,再将绕点顺时针旋转,使点落在直线上即可,求旋转的角度.(参考数据:,,,,,,
北师大版初中数学九年级下册第1章直角三角形的边角关系1.5 三角函数的应用同步练习(一)(含答案)
参考答案与试题解析
一.选择题
1.解:由题意:,
,
,
故选:.
2.解:栏杆端升高的高度(米,
故选:.
3.解:如图,过点作于点,
根据题意可知:
当太阳光线与垂直时,遮阳效果最佳,
,
,,
,
,
,
,
为的中点,
,
,
,
.
所以要遮阳效果最佳的长约为1.5米.
故选:.
4.解:连接,,过作交于点,
,是光盘与桌面的切点,
,
,
,
是的中点,
在中,
,
;
故选:.
5.解:由题意可得,
立柱根部与圭表的冬至线的距离为:,
故选:.
6.解:如图,,
,
,
,
,
作,垂足为,
则.
,
,
,
折叠后重叠部分的面积为.
故选:.
二.填空题
7.解:因为坡度比为,即,
.
则其下降的高度(米.
8.解:在中,
,
(米,
答:大厅两层之间的距离的长约为6.2米.
故答案为:6.2.
9.解:如图,过点作水平面的垂线,垂足为,
根据题意可知:
,,
设,则,
根据勾股定理,得
,
即,
解得,
所以.
故答案为:.
10.解:在直角三角形中,,
,
在直角三角形中,,
,
两次测量的影长差(米,
故答案为:10.
11.解:由题意可得,
,
故答案为:
12.解:如图2,①过点作于点,
图1中,
,且,
,
,
,
图2中,,
,
,
又,,
,
,
,
②,
,
设、与桌面交于点、,
是等腰直角三角形,
是斜边上的高,
所以,
所以台灯照在桌面上的最大面积是半径为20的圆的面积为:
故答案为:、.
三.解答题
13.解:(1)如图,作于,则四边形、为矩形,
,.
,
,
;
(2)在中,.
,
,
此时凳子中心到墙的距离约为.
14.解:如图(3),
过点作于点,
过点作于点,
,,
,
过点作于点,
,,
,
,
,
,
如图(2)中,
,
,
表示端点到地面的距离,
.
答:端点到地面的距离为.
15.
解:(1)过作于..
,,
,,
,
,
,
,
,
,
;
(2)过作交的延长线于,
,
答:拉杆端点到水平滑杆的距离为.
16.解:(1)如图2,过作,交的延长线于点,过点作,垂足为,过点作,垂足为,
由题意可知,,,,,
在中,,
,
又,
,
,,
,
,
,
在中,,
,
答:点到直线的距离约为;
(2)旋转后,如图3所示,根据题意可知,
在中,,,
,
,
因此旋转的角度约为:,
答:旋转的角度约为.
_21?????????è?????(www.21cnjy.com)_
北师大版初中数学九年级下册第1章直角三角形的边角关系
1.5 三角函数的应用同步练习(一)
一.选择题
1.如图所示,河堤横断面迎水坡的坡比是,堤高,则迎水坡宽度的长为
A. B. C. D.
2.如图,某停车场入口的栏杆,从水平位置绕点旋转到的位置,已知的长为3米.若栏杆的旋转,则栏杆端升高的高度为
A.米 B.米 C.米 D.米
3.如图,滑动调节式遮阳伞的立柱垂直于地面,为立柱上的滑动调节点,伞体的截面示意图为,为的中点,,,,.根据生活经验,当太阳光线与垂直时,遮阳效果最佳,在上午时,太阳光线与地面的夹角为,若要遮阳效果最佳的长约为
(参考数据:,,,
A. B. C. D.
4.如图,一块直角三角板和一张光盘竖放在桌面上,其中是光盘与桌面的切点,,光盘的直径是,则斜边被光盘截得的线段长为
A. B. C. D.
5.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表,如图是一个根据长春的地理位置设计的圭表,其中,立柱的高为,已知冬至时长春的正午光入射角约为,则立柱根部与圭表的冬至线的距离(距的长)约为
A. B. C. D.
6.如图,将宽为的纸条沿折叠,使,则折叠后重叠部分的面积为
A. B. C. D.
二.填空题
7.如图,一人乘雪橇沿坡比的斜坡笔直滑下72米,那么他下降的高度为 米.
8.如图,某商店营业大厅自动扶梯的倾斜角为,的长为12米,则大厅两层之间的高度为 米.(结果保留一位小数)【参考数据:,,】
9.如图是一斜坡的横截面,某人沿着坡度为的斜坡从点向上走了5米到点处,则此时人离水平面的垂直高度为 .
10.如图,校园内有一棵与地面垂直的树,树高为米,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成角时,第二次是阳光与地面成角时,则两次测量的影长差为 米.
11.港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术而闻名世界.其主体工程青州航道桥是一座双塔双索面钢箱梁斜拉桥,两座索塔及索塔两侧的斜拉索对称分布,塔高为163米,大桥主跨的中点为,记斜拉索与大桥主梁所夹锐角为,那么用塔高和的三角函数表示主跨的长为 米.
12.如图是某种台灯的示意图,可弯曲,根据测量,灯罩的截面是等腰直角三角形,此时很大一部分光照向远方而没有射在桌面上,若使绕转轴顺时针转动,可使台灯的光更多地落在桌面上.如图,现测得,且,灯心到桌面的距离,则此时 .若继续转动使与灯柱垂直,则此时台灯照在桌面上的最大面积为 .
三.解答题
13.疫情期间部分学生选择在家用电视观看网络课程,为了保护眼睛,电视机的安装高度有一定的要求.如图所示,小嘉家的壁挂电视机的安装高度为1米,电视的中心位置的中点)比平视视线低(这样观看眼睛最不容易疲劳),电视机宽度为,眼到凳子平面的高度为.
(1)求小嘉应选用凳子的高度;
(2)若看电视的视角为时,观看感最好,求此时凳子中心到墙的距离(电视机的厚度忽略不计).(参考数据:,,
14.如今,不少人购买家具时追求简约大气的风格,图(1)是一款非常畅销的简约落地收纳镜,其支架的形状固定不变,镜面可随意选择,图(2)为其侧面示意图,其中为镜面,为放置物品的收纳架,,为等长的支架,为水平地面,且,,,,如图(3)将镜面顺时针旋转,求此时收纳镜顶部端点到地面的距离.(结果精确到,参考数据:,,,,
15.如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆、箱长、拉杆的长度都相等,即,点、在线段上,点在上,支杆,,,.
请根据以上信息,解决下列问题;
(1)求的长度(结果保留根号);
(2)求拉杆端点到水平滑杆的距离(结果保留到.
参考数据:,,.
16.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.量得托板长,支撑板长,底座长.托板固定在支撑板顶端点处,且,托板可绕点转动,支撑板可绕点转动.(结果保留小数点后一位)
(1)若,,求点到直线的距离;
(2)为了观看舒适,在(1)的情况下,把绕点逆时针旋转后,再将绕点顺时针旋转,使点落在直线上即可,求旋转的角度.(参考数据:,,,,,,
北师大版初中数学九年级下册第1章直角三角形的边角关系1.5 三角函数的应用同步练习(一)(含答案)
参考答案与试题解析
一.选择题
1.解:由题意:,
,
,
故选:.
2.解:栏杆端升高的高度(米,
故选:.
3.解:如图,过点作于点,
根据题意可知:
当太阳光线与垂直时,遮阳效果最佳,
,
,,
,
,
,
,
为的中点,
,
,
,
.
所以要遮阳效果最佳的长约为1.5米.
故选:.
4.解:连接,,过作交于点,
,是光盘与桌面的切点,
,
,
,
是的中点,
在中,
,
;
故选:.
5.解:由题意可得,
立柱根部与圭表的冬至线的距离为:,
故选:.
6.解:如图,,
,
,
,
,
作,垂足为,
则.
,
,
,
折叠后重叠部分的面积为.
故选:.
二.填空题
7.解:因为坡度比为,即,
.
则其下降的高度(米.
8.解:在中,
,
(米,
答:大厅两层之间的距离的长约为6.2米.
故答案为:6.2.
9.解:如图,过点作水平面的垂线,垂足为,
根据题意可知:
,,
设,则,
根据勾股定理,得
,
即,
解得,
所以.
故答案为:.
10.解:在直角三角形中,,
,
在直角三角形中,,
,
两次测量的影长差(米,
故答案为:10.
11.解:由题意可得,
,
故答案为:
12.解:如图2,①过点作于点,
图1中,
,且,
,
,
,
图2中,,
,
,
又,,
,
,
,
②,
,
设、与桌面交于点、,
是等腰直角三角形,
是斜边上的高,
所以,
所以台灯照在桌面上的最大面积是半径为20的圆的面积为:
故答案为:、.
三.解答题
13.解:(1)如图,作于,则四边形、为矩形,
,.
,
,
;
(2)在中,.
,
,
此时凳子中心到墙的距离约为.
14.解:如图(3),
过点作于点,
过点作于点,
,,
,
过点作于点,
,,
,
,
,
,
如图(2)中,
,
,
表示端点到地面的距离,
.
答:端点到地面的距离为.
15.
解:(1)过作于..
,,
,,
,
,
,
,
,
,
;
(2)过作交的延长线于,
,
答:拉杆端点到水平滑杆的距离为.
16.解:(1)如图2,过作,交的延长线于点,过点作,垂足为,过点作,垂足为,
由题意可知,,,,,
在中,,
,
又,
,
,,
,
,
,
在中,,
,
答:点到直线的距离约为;
(2)旋转后,如图3所示,根据题意可知,
在中,,,
,
,
因此旋转的角度约为:,
答:旋转的角度约为.
_21?????????è?????(www.21cnjy.com)_
