26.2.2 实际问题与反比例函数 同步练习(含解析)
文档属性
| 名称 | 26.2.2 实际问题与反比例函数 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 09:02:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(二)
一.选择题
1.一司机驾驶汽车从甲地去乙地,他以80千米时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度(千米时)与时间(小时)的函数关系为
A. B. C. D.
2.面积是160平方米的长方形,它的长米,宽米之间的关系表达式是
A. B. C. D.
3.矩形面积是,设它的一边长为,则矩形的另一边长与的函数关系是
A. B. C. D.
4.验光师测得一组关于近视眼镜的度数(度与镜片焦距(米的对应数据如下表,根据表中数据,可得关于的函数表达式为
近视眼镜的度数(度 200 250 400 500 1000
镜片焦距(米 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
5.已知某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,当气球内的气压大于时,气球将爆炸.为了安全起见,气球的体积应
A.不小于 B.小于 C.不小于 D.小于
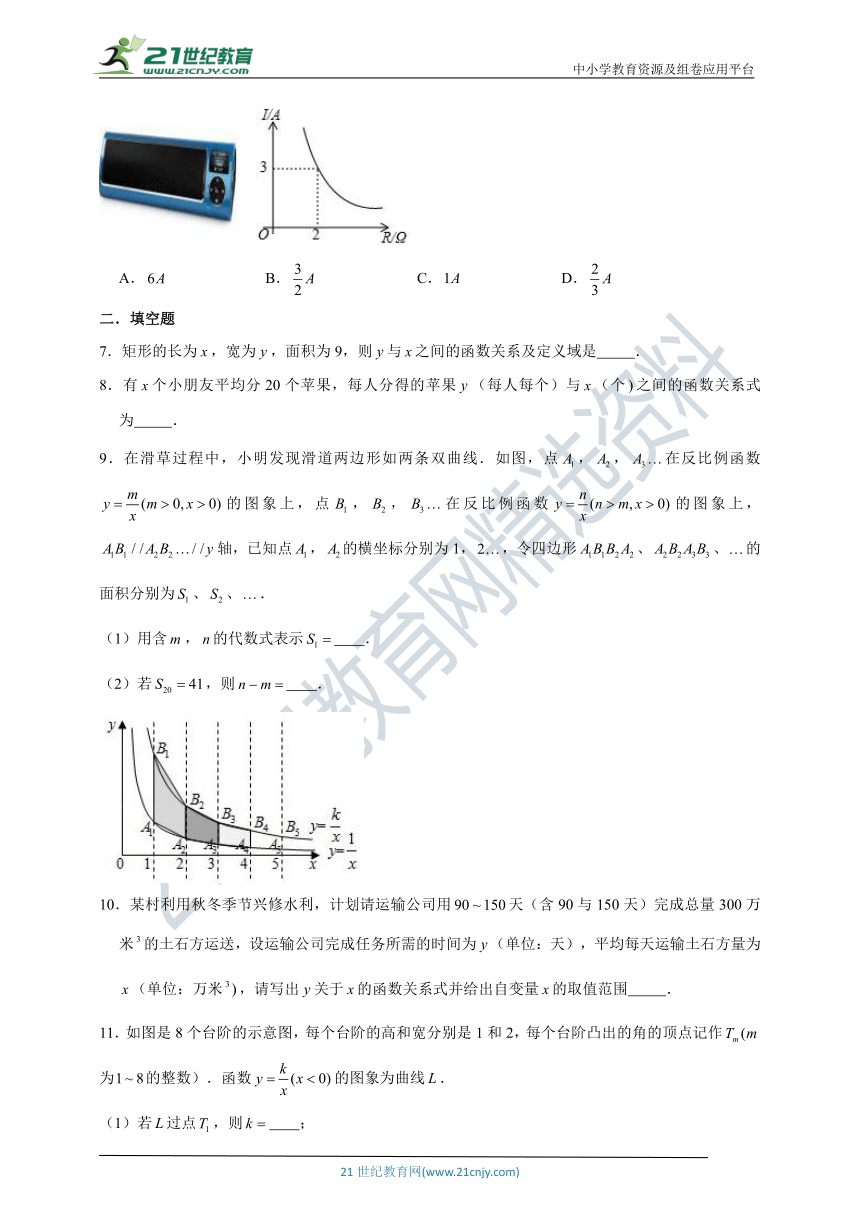
6.一款便携式音箱以锂电池作为电源,该电池的电压为定值,工作时电流(单位:与电阻(单位:之间的函数关系如图所示,则当电阻为时,电流为
A. B. C. D.
二.填空题
7.矩形的长为,宽为,面积为9,则与之间的函数关系及定义域是 .
8.有个小朋友平均分20个苹果,每人分得的苹果(每人每个)与(个之间的函数关系式为 .
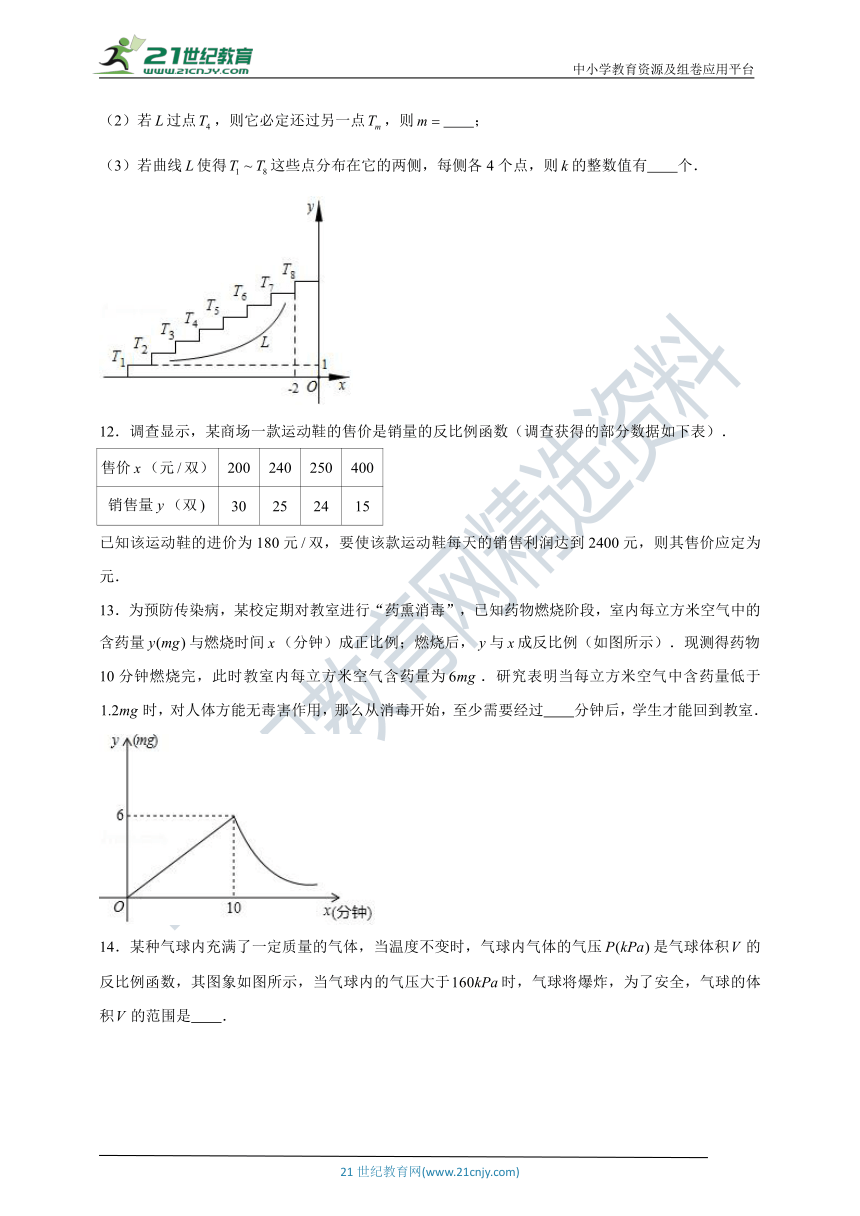
9.在滑草过程中,小明发现滑道两边形如两条双曲线.如图,点,,在反比例函数的图象上,点,,在反比例函数的图象上,轴,已知点,的横坐标分别为1,,令四边形、、的面积分别为、、.
(1)用含,的代数式表示 .
(2)若,则 .
10.某村利用秋冬季节兴修水利,计划请运输公司用天(含90与150天)完成总量300万米的土石方运送,设运输公司完成任务所需的时间为(单位:天),平均每天运输土石方量为(单位:万米,请写出关于的函数关系式并给出自变量的取值范围 .
11.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作为的整数).函数的图象为曲线.
(1)若过点,则 ;
(2)若过点,则它必定还过另一点,则 ;
(3)若曲线使得这些点分布在它的两侧,每侧各4个点,则的整数值有 个.
12.调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价(元双) 200 240 250 400
销售量(双 30 25 24 15
已知该运动鞋的进价为180元双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
13.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量与燃烧时间(分钟)成正比例;燃烧后,与成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为.研究表明当每立方米空气中含药量低于时,对人体方能无毒害作用,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室.
14.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气球体积的反比例函数,其图象如图所示,当气球内的气压大于时,气球将爆炸,为了安全,气球的体积的范围是 .
三.解答题
15.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为时,气压是多少?
(3)当气球内的气压大于时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到
16.用函数解析式表示下列问题中变量间的对应关系:
一个游泳池的容积为立方,游泳池注满水的时间(单位:随注水速度的变化而变化.
17.疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价(元与日销售量(只之间有如下关系:
日销售单价(元 3 4 5 6
日销售量(只 2000 1500 1200 1000
(1)猜测并确定与之间的函数关系式;
(2)设经营此口罩的销售利润为元,求出与之间的函数关系式,
(3)若物价局规定此口罩的售价最高不能超过10元只,请你求出当日销售单价定为多少时,才能获得最大日销售利润?最大利润是多少元?
18.在面积都相等的所有矩形中,当其中一个矩形的一边长为4时,它的另一边长为6.
(1)设矩形的相邻两边长分别为,,
①求关于的函数表达式;
②当时,求的取值范围.
(2)是否有一个矩形的周长为24?如果没有请说明理由,如果有,请求出边长.
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(二)(含答案)
参考答案与试题解析
一.选择题
1.解:由于以80千米时的平均速度用了6小时到达目的地,那么路程为千米,
汽车的速度(千米时)与时间(小时)的函数关系为.
故选:.
2.解:根据题意:
,
故选:.
3.解:由于矩形的另一边长矩形面积一边长,
矩形的另一边长与的函数关系是.
故选:.
4.解:由表格中数据可得:,
故关于的函数表达式为:.
故选:.
5.解:设球内气体的气压和气体体积的关系式为
图象过点
即在第一象限内,随的增大而减小,
当时,.
故选:.
6.解:设用电阻表示电流的函数解析式为,
反比例函数图象过,
,
,
当时,,
故选:.
二.填空题
7.解:矩形的长为,宽为,面积为9,
,且,
则与之间的函数关系及定义域是:.
故答案为:.
8.解:每人分得的苹果(每人每个)与(个之间的函数关系式为.
故答案为:.
9.解:(1)轴,
和的横坐标相等,和的横坐标相等,,和的横坐标相等,
点,的横坐标分别为1,2,,
点,的横坐标分别为1,2,,
点,,在反比例函数的图象上,点,,反比例函数的图象上,
,,
,
故答案为:;
(2)由(1)同理得:,,,
,
,
,
,
,
,
解得:,
故答案为:840.
10.解:由题意得,,
把代入,得,
把代入,得,
所以自变量的取值范围为:,
故答案为.
11.解:(1)每个台阶的高和宽分别是1和2,
,,,,,,,,
过点,
,
故答案为:;
(2)过点,
,
反比例函数解析式为:,
当时,,
在反比例函数图象上,
,
故答案为:5;
(3)若曲线过点,时,,
若曲线过点,时,,
若曲线过点,时,,
若曲线过点,时,,
曲线使得这些点分布在它的两侧,每侧各4个点,
,
整数,,,,,,共7个,
答案为:7.
12.答案:300.
解:由表中数据得:,
,
则所求函数关系式为;
由题意得:,
把代入得:,
解得:,
经检验,是原方程的根,
答:若计划每天的销售利润为2400元,则其单价应定为300元.
故答案为:300.
13.解:设药物燃烧后与之间的解析式,把点代入得,解得,
关于的函数式为:;
当时,由;得,所以50分钟后学生才可进入教室;
故答案为:50.
14.解:设球内气体的气压和气体体积的关系式为,
图象过点,
,
即,在第一象限内,随的增大而减小,
当时,.
故答案为:.
三.解答题
15.解:(1)设,
由题意知,
所以,
故;
(2)当时,;
(3)当时,.
所以为了安全起见,气体的体积应不少于.
16.解:由题意得,
整理得.
17.解:(1)由表可知,,
;
(2)根据题意,得:
;
(3),
,
即当时,取得最大值,最大值为4800元,
答:当日销售单价定为10元个时,才能获得最大日销售利润,最大利润是4800元.
18.解:(1)①由题意知,即,
;
②当时,,
当时,;
(2)矩形的周长为24,
设矩形的长为,则宽为,
,
解得,
边长为,.
_21?????????è?????(www.21cnjy.com)_
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(二)
一.选择题
1.一司机驾驶汽车从甲地去乙地,他以80千米时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度(千米时)与时间(小时)的函数关系为
A. B. C. D.
2.面积是160平方米的长方形,它的长米,宽米之间的关系表达式是
A. B. C. D.
3.矩形面积是,设它的一边长为,则矩形的另一边长与的函数关系是
A. B. C. D.
4.验光师测得一组关于近视眼镜的度数(度与镜片焦距(米的对应数据如下表,根据表中数据,可得关于的函数表达式为
近视眼镜的度数(度 200 250 400 500 1000
镜片焦距(米 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
5.已知某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,当气球内的气压大于时,气球将爆炸.为了安全起见,气球的体积应
A.不小于 B.小于 C.不小于 D.小于
6.一款便携式音箱以锂电池作为电源,该电池的电压为定值,工作时电流(单位:与电阻(单位:之间的函数关系如图所示,则当电阻为时,电流为
A. B. C. D.
二.填空题
7.矩形的长为,宽为,面积为9,则与之间的函数关系及定义域是 .
8.有个小朋友平均分20个苹果,每人分得的苹果(每人每个)与(个之间的函数关系式为 .
9.在滑草过程中,小明发现滑道两边形如两条双曲线.如图,点,,在反比例函数的图象上,点,,在反比例函数的图象上,轴,已知点,的横坐标分别为1,,令四边形、、的面积分别为、、.
(1)用含,的代数式表示 .
(2)若,则 .
10.某村利用秋冬季节兴修水利,计划请运输公司用天(含90与150天)完成总量300万米的土石方运送,设运输公司完成任务所需的时间为(单位:天),平均每天运输土石方量为(单位:万米,请写出关于的函数关系式并给出自变量的取值范围 .
11.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作为的整数).函数的图象为曲线.
(1)若过点,则 ;
(2)若过点,则它必定还过另一点,则 ;
(3)若曲线使得这些点分布在它的两侧,每侧各4个点,则的整数值有 个.
12.调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价(元双) 200 240 250 400
销售量(双 30 25 24 15
已知该运动鞋的进价为180元双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
13.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量与燃烧时间(分钟)成正比例;燃烧后,与成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为.研究表明当每立方米空气中含药量低于时,对人体方能无毒害作用,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室.
14.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气球体积的反比例函数,其图象如图所示,当气球内的气压大于时,气球将爆炸,为了安全,气球的体积的范围是 .
三.解答题
15.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为时,气压是多少?
(3)当气球内的气压大于时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到
16.用函数解析式表示下列问题中变量间的对应关系:
一个游泳池的容积为立方,游泳池注满水的时间(单位:随注水速度的变化而变化.
17.疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价(元与日销售量(只之间有如下关系:
日销售单价(元 3 4 5 6
日销售量(只 2000 1500 1200 1000
(1)猜测并确定与之间的函数关系式;
(2)设经营此口罩的销售利润为元,求出与之间的函数关系式,
(3)若物价局规定此口罩的售价最高不能超过10元只,请你求出当日销售单价定为多少时,才能获得最大日销售利润?最大利润是多少元?
18.在面积都相等的所有矩形中,当其中一个矩形的一边长为4时,它的另一边长为6.
(1)设矩形的相邻两边长分别为,,
①求关于的函数表达式;
②当时,求的取值范围.
(2)是否有一个矩形的周长为24?如果没有请说明理由,如果有,请求出边长.
人教版初中数学九年级下册第26章 反比例函数
26.2 实际问题与反比例函数同步练习(二)(含答案)
参考答案与试题解析
一.选择题
1.解:由于以80千米时的平均速度用了6小时到达目的地,那么路程为千米,
汽车的速度(千米时)与时间(小时)的函数关系为.
故选:.
2.解:根据题意:
,
故选:.
3.解:由于矩形的另一边长矩形面积一边长,
矩形的另一边长与的函数关系是.
故选:.
4.解:由表格中数据可得:,
故关于的函数表达式为:.
故选:.
5.解:设球内气体的气压和气体体积的关系式为
图象过点
即在第一象限内,随的增大而减小,
当时,.
故选:.
6.解:设用电阻表示电流的函数解析式为,
反比例函数图象过,
,
,
当时,,
故选:.
二.填空题
7.解:矩形的长为,宽为,面积为9,
,且,
则与之间的函数关系及定义域是:.
故答案为:.
8.解:每人分得的苹果(每人每个)与(个之间的函数关系式为.
故答案为:.
9.解:(1)轴,
和的横坐标相等,和的横坐标相等,,和的横坐标相等,
点,的横坐标分别为1,2,,
点,的横坐标分别为1,2,,
点,,在反比例函数的图象上,点,,反比例函数的图象上,
,,
,
故答案为:;
(2)由(1)同理得:,,,
,
,
,
,
,
,
解得:,
故答案为:840.
10.解:由题意得,,
把代入,得,
把代入,得,
所以自变量的取值范围为:,
故答案为.
11.解:(1)每个台阶的高和宽分别是1和2,
,,,,,,,,
过点,
,
故答案为:;
(2)过点,
,
反比例函数解析式为:,
当时,,
在反比例函数图象上,
,
故答案为:5;
(3)若曲线过点,时,,
若曲线过点,时,,
若曲线过点,时,,
若曲线过点,时,,
曲线使得这些点分布在它的两侧,每侧各4个点,
,
整数,,,,,,共7个,
答案为:7.
12.答案:300.
解:由表中数据得:,
,
则所求函数关系式为;
由题意得:,
把代入得:,
解得:,
经检验,是原方程的根,
答:若计划每天的销售利润为2400元,则其单价应定为300元.
故答案为:300.
13.解:设药物燃烧后与之间的解析式,把点代入得,解得,
关于的函数式为:;
当时,由;得,所以50分钟后学生才可进入教室;
故答案为:50.
14.解:设球内气体的气压和气体体积的关系式为,
图象过点,
,
即,在第一象限内,随的增大而减小,
当时,.
故答案为:.
三.解答题
15.解:(1)设,
由题意知,
所以,
故;
(2)当时,;
(3)当时,.
所以为了安全起见,气体的体积应不少于.
16.解:由题意得,
整理得.
17.解:(1)由表可知,,
;
(2)根据题意,得:
;
(3),
,
即当时,取得最大值,最大值为4800元,
答:当日销售单价定为10元个时,才能获得最大日销售利润,最大利润是4800元.
18.解:(1)①由题意知,即,
;
②当时,,
当时,;
(2)矩形的周长为24,
设矩形的长为,则宽为,
,
解得,
边长为,.
_21?????????è?????(www.21cnjy.com)_
