九年级数学圆周角的练习题
文档属性
| 名称 | 九年级数学圆周角的练习题 |  | |
| 格式 | rar | ||
| 文件大小 | 330.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-25 21:52:57 | ||
图片预览




文档简介
(共26张PPT)
24.1.4 圆周角(2)
回顾:圆周角定理及推论?
思考:判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°角所对的弦是直径( )
4.直径所对的角等于90°( )
5.长等于半径的弦所对的圆周角等于30°( )
√
√
√
×
×
·
A
B
C1
O
C2
C3
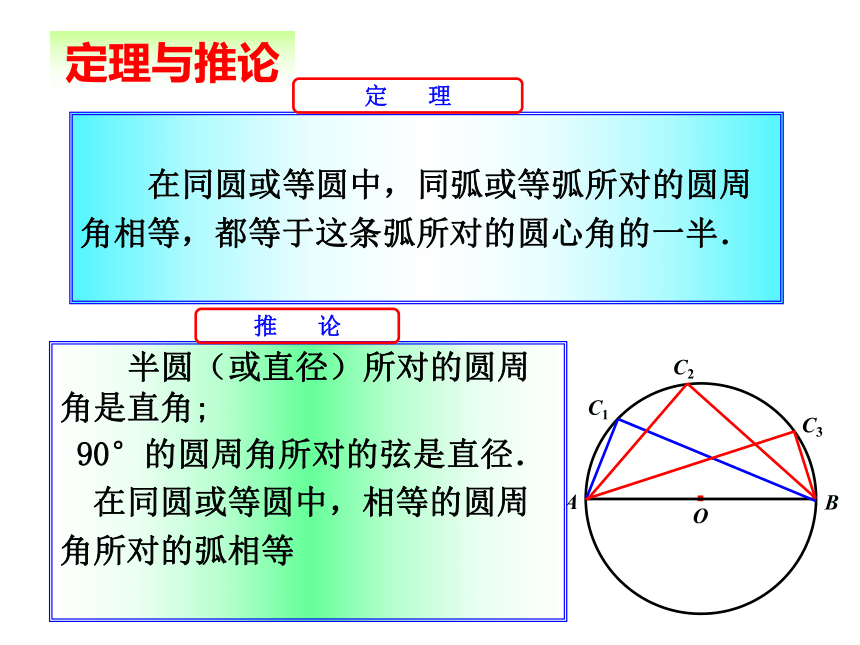
定理与推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定 理
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
在同圆或等圆中,相等的圆周角所对的弧相等
推 论
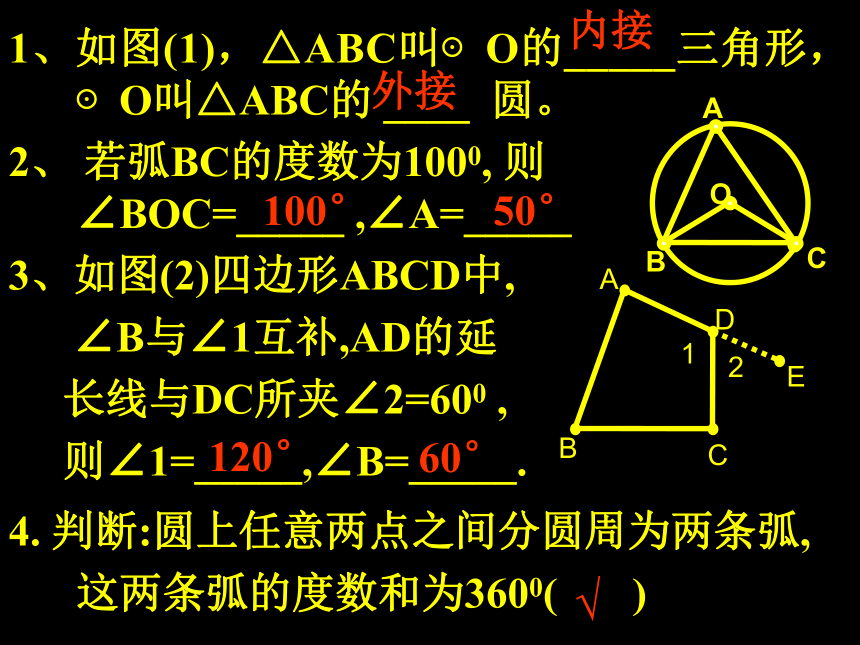
1、如图(1),△ABC叫⊙O的_____三角形,⊙O叫△ABC的 ____ 圆。
2、 若弧BC的度数为1000, 则∠BOC=_____ ,∠A=_____
3、如图(2)四边形ABCD中,
∠B与∠1互补,AD的延
长线与DC所夹∠2=600 ,
则∠1=_____,∠B=_____.
4. 判断:圆上任意两点之间分圆周为两条弧,这两条弧的度数和为3600( )
内接
外接
100°
50°
120°
60°
√
A
B
C
O
E
D
C
B
A
2
1
新课讲解:
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
O
B
C
D
E
F
A
O
A
C
D
E
B
O
C
A
B
D
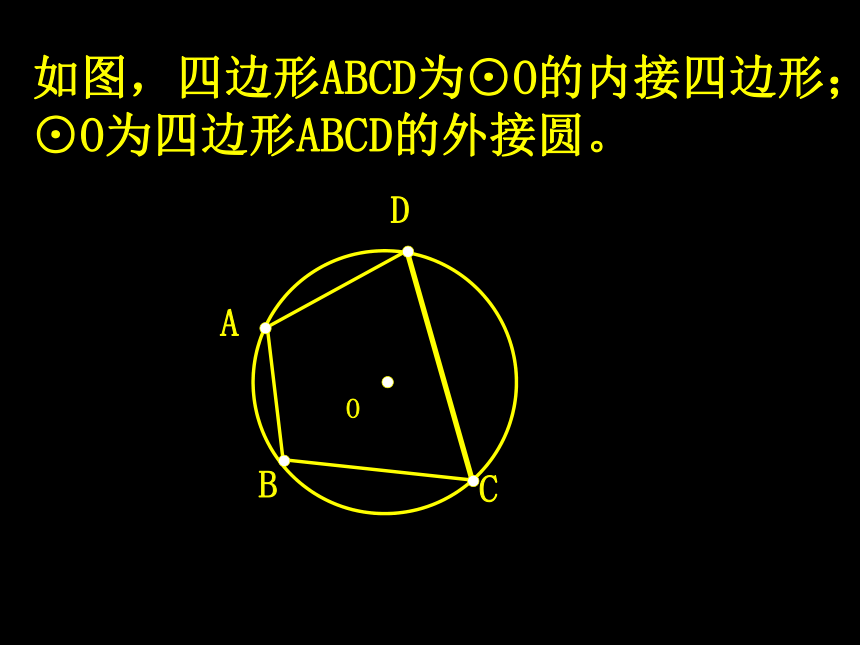
如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
O
C
D
B
A
如图:圆内接四边形ABCD中,
∴∠A+∠ C= 180°
同理∠B+∠D=180°
圆的内接四边形的对角互补。
O
C
A
B
D
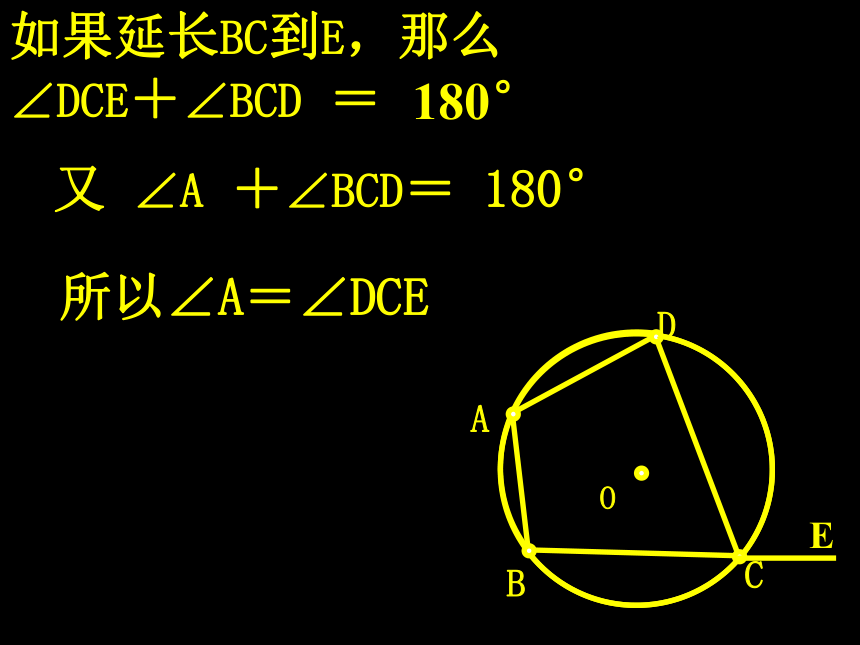
如果延长BC到E,那么∠DCE+∠BCD =
180°
所以∠A=∠DCE
又 ∠A +∠BCD= 180°
C
O
D
B
A
E
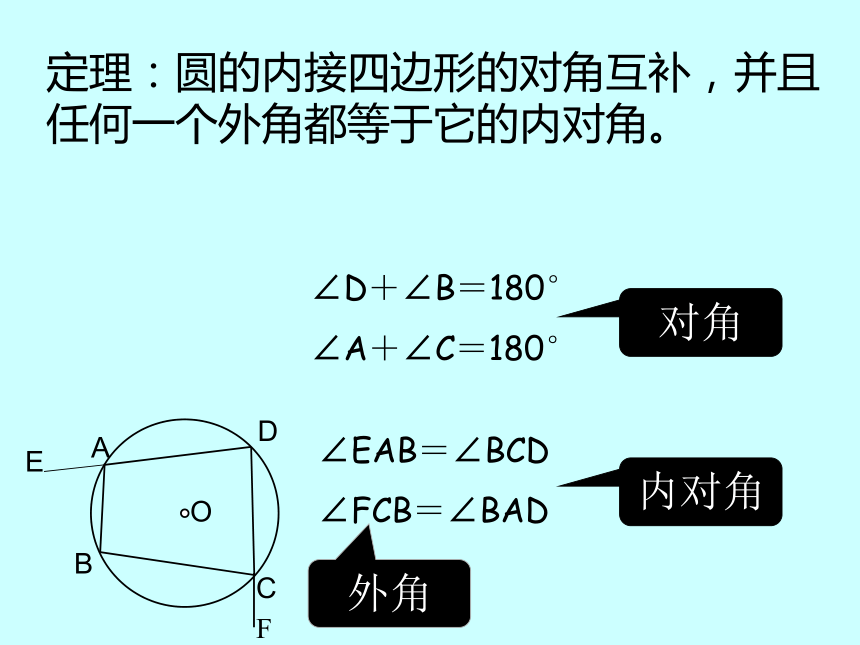
定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
C
B
A
D
O
E
F
∠D+∠B=180°
∠A+∠C=180°
∠EAB=∠BCD
∠FCB=∠BAD
对角
外角
内对角
因为∠A是与∠2相邻的内角∠1的对角,我们把∠A叫做∠DCE的内对角。
圆内接四边形的一个外角等于它的内对角。
C
O
D
B
A
E
1
2
定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
几何表达式:
∵ ABCD是⊙O的内接四边形,
∴ ∠A+∠C=180°
且∠B=∠1
D
A
B
C
1
E
(1)四边形ABCD内接于⊙O,则∠A+∠C=______ ∠B+∠ADC=_______;若∠B=80°,则∠ADC=____ ∠CDE=______
(2)四边形ABCD内接于⊙O,∠AOC=100° 则∠B=______∠D=______
(3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____,
180°
180°
100°
80°
50°
130°
45°
E
D
B
A
C
80
D
B
A
C
O
100
若ABCD为圆内接四边形,则下列哪个选项可能成立( )
(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
(B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
(C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
(D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
B
补充练习:
(4)梯形ABCD内接于⊙O,AD∥BC, ∠B=750,则∠C=_____
75°
返回
圆的内接梯形一定是_____梯形。
D
B
A
C
O
1、如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A、115° B、130°
C、65° D、50°
2、 如图,等边三角形ABC内
接于⊙O,P是AB上的
一点,则∠APB= 。
A
B
D
C
O
⌒
A
P
B
C
3、圆内接梯形ABCD中,AD∥BC,∠B=75°,则∠C= °
4、已知四边形ABCD内接于⊙O,且∠A:∠B:∠C =2:3:4,求∠D的度数.
5、圆的内接四边形ABCD中,AC垂直平分BD,∠BAC=40 °,
则∠BCD= °
6、四边形ABCD内接于⊙O,BA、CD的延长线交于P,AD=2cm,BC=3cm,PA=4cm,求PC的长.
例 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。
求证:CE∥DF
1
2
O
O
F
A
B
E
C
D
1
CE∥DF
∠E+∠F=180°
∠E+∠1=180°、∠1=∠F
ABEC是⊙O1的内接四边形
ABFD是⊙O2的内接四边形
连结AB
1
2
O
O
F
A
B
E
C
D
1
证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE ∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果?
1)延长EF,是否有
∠E=∠BAD= ∠1 ?
延长DF, 能否证明
∠E=∠2=∠3?
巩固练习:
1、如图,四边形ABCD为⊙O 的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。
A
O
D
B
C
O
C
D
B
A
已知:如图,四边形ABCD是圆的内接四边形并且ABCD是平行四边形。
求证:四边形ABCD
是矩形。
例 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
例题
3.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)
·
A
B
C
O
求证: △ABC 为直角三角形.
证明:
CO= AB,
以AB为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴∠ACB= ×180°= 90°.
已知:△ABC 中,CO为AB边上的中线,
且CO= AB
∴ △ABC 为直角三角形.
课本 练 习
如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.
D
A
B
C
O
O
O
·
方法一
方法二
方法三
方法四
A
B
练 习
拓展练习
如图,点P是⊙O外一点,点A、B、Q是⊙O上的点。(1)求证∠P< ∠AQB
(2)如果点P在⊙O内, ∠P与∠AQB有怎样的关系?为什么?
24.1.4 圆周角(2)
回顾:圆周角定理及推论?
思考:判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°角所对的弦是直径( )
4.直径所对的角等于90°( )
5.长等于半径的弦所对的圆周角等于30°( )
√
√
√
×
×
·
A
B
C1
O
C2
C3
定理与推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定 理
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
在同圆或等圆中,相等的圆周角所对的弧相等
推 论
1、如图(1),△ABC叫⊙O的_____三角形,⊙O叫△ABC的 ____ 圆。
2、 若弧BC的度数为1000, 则∠BOC=_____ ,∠A=_____
3、如图(2)四边形ABCD中,
∠B与∠1互补,AD的延
长线与DC所夹∠2=600 ,
则∠1=_____,∠B=_____.
4. 判断:圆上任意两点之间分圆周为两条弧,这两条弧的度数和为3600( )
内接
外接
100°
50°
120°
60°
√
A
B
C
O
E
D
C
B
A
2
1
新课讲解:
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
O
B
C
D
E
F
A
O
A
C
D
E
B
O
C
A
B
D
如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
O
C
D
B
A
如图:圆内接四边形ABCD中,
∴∠A+∠ C= 180°
同理∠B+∠D=180°
圆的内接四边形的对角互补。
O
C
A
B
D
如果延长BC到E,那么∠DCE+∠BCD =
180°
所以∠A=∠DCE
又 ∠A +∠BCD= 180°
C
O
D
B
A
E
定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
C
B
A
D
O
E
F
∠D+∠B=180°
∠A+∠C=180°
∠EAB=∠BCD
∠FCB=∠BAD
对角
外角
内对角
因为∠A是与∠2相邻的内角∠1的对角,我们把∠A叫做∠DCE的内对角。
圆内接四边形的一个外角等于它的内对角。
C
O
D
B
A
E
1
2
定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
几何表达式:
∵ ABCD是⊙O的内接四边形,
∴ ∠A+∠C=180°
且∠B=∠1
D
A
B
C
1
E
(1)四边形ABCD内接于⊙O,则∠A+∠C=______ ∠B+∠ADC=_______;若∠B=80°,则∠ADC=____ ∠CDE=______
(2)四边形ABCD内接于⊙O,∠AOC=100° 则∠B=______∠D=______
(3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____,
180°
180°
100°
80°
50°
130°
45°
E
D
B
A
C
80
D
B
A
C
O
100
若ABCD为圆内接四边形,则下列哪个选项可能成立( )
(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
(B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
(C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
(D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
B
补充练习:
(4)梯形ABCD内接于⊙O,AD∥BC, ∠B=750,则∠C=_____
75°
返回
圆的内接梯形一定是_____梯形。
D
B
A
C
O
1、如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A、115° B、130°
C、65° D、50°
2、 如图,等边三角形ABC内
接于⊙O,P是AB上的
一点,则∠APB= 。
A
B
D
C
O
⌒
A
P
B
C
3、圆内接梯形ABCD中,AD∥BC,∠B=75°,则∠C= °
4、已知四边形ABCD内接于⊙O,且∠A:∠B:∠C =2:3:4,求∠D的度数.
5、圆的内接四边形ABCD中,AC垂直平分BD,∠BAC=40 °,
则∠BCD= °
6、四边形ABCD内接于⊙O,BA、CD的延长线交于P,AD=2cm,BC=3cm,PA=4cm,求PC的长.
例 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。
求证:CE∥DF
1
2
O
O
F
A
B
E
C
D
1
CE∥DF
∠E+∠F=180°
∠E+∠1=180°、∠1=∠F
ABEC是⊙O1的内接四边形
ABFD是⊙O2的内接四边形
连结AB
1
2
O
O
F
A
B
E
C
D
1
证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE ∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果?
1)延长EF,是否有
∠E=∠BAD= ∠1 ?
延长DF, 能否证明
∠E=∠2=∠3?
巩固练习:
1、如图,四边形ABCD为⊙O 的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。
A
O
D
B
C
O
C
D
B
A
已知:如图,四边形ABCD是圆的内接四边形并且ABCD是平行四边形。
求证:四边形ABCD
是矩形。
例 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
例题
3.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)
·
A
B
C
O
求证: △ABC 为直角三角形.
证明:
CO= AB,
以AB为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴∠ACB= ×180°= 90°.
已知:△ABC 中,CO为AB边上的中线,
且CO= AB
∴ △ABC 为直角三角形.
课本 练 习
如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.
D
A
B
C
O
O
O
·
方法一
方法二
方法三
方法四
A
B
练 习
拓展练习
如图,点P是⊙O外一点,点A、B、Q是⊙O上的点。(1)求证∠P< ∠AQB
(2)如果点P在⊙O内, ∠P与∠AQB有怎样的关系?为什么?
同课章节目录
