整式的加减
图片预览






文档简介
(共19张PPT)
整式的加减
合并同类项
整式的加减
中学阶段是人生道路上的加油站
一.温故而知新
1.请任意写一个单项式,并写出这个单项式的系数和次数。
2.将同小组同学写出的单项式写在一起,就变成了一个新的式子,观察这个式子的组成可以分为哪两部分?
3.我们发现:无论怎么分,都是两个整式的和,今天,我们一起来研究有关整式的和的问题。
252t
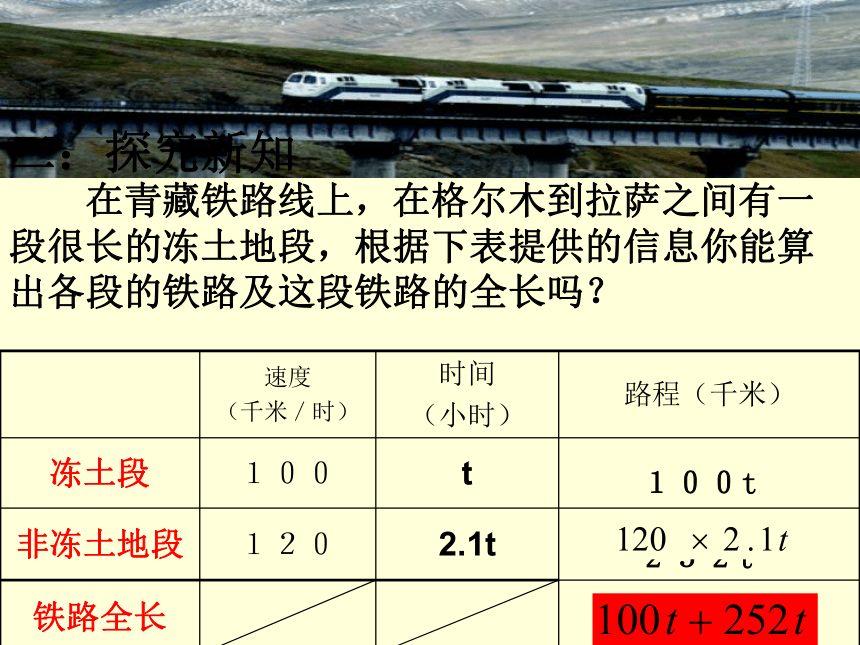
在青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段,根据下表提供的信息你能算出各段的铁路及这段铁路的全长吗?
二:探究新知
速度
(千米/时) 时间
(小时) 路程(千米)
冻土段 100 t
非冻土地段 120 2.1t
铁路全长
100t
+
能化简吗?依据是什么?
单项式
单项式
整式
整式
+
还记得乘法分配律吗?用字母如何表示?
一个数与几个数的和相乘,等于这个数与和的每个加数的积的和。
用字母可以表示为
a(b+c)=ab+ac
如果把这个等式两边交换位置就变成了
ab+ac= a(b+c)
探究
(1)计算
100x2+252x2=———
100x(-2)+252X(-2)=———
(2)观察式子:100t+252t,分析它的构成与(1)中两个算式有何异同?
相同点:都形如ba+ca,在每个算式里都有相同因数
不同点:(1)中相同因数都是数字因数,(2)中相同因数是字母因数
想一想:能否应用等式ab+ac=a(b+c)来对式子100t+252t化简呢?为什么?
学习上节课 阅读与思考 栏目时,我们已经知道:随着实践的发展,代数学的基础使用字母表示数,它首要研究的就是用字母表示的式子的运算法则和方程的解法
我们知道:字母虽然不是具体的数,但是它可以表示各种各样的数,包括整式,那么化简100t+252t就不是一件困难的事情了
100t+252t=(100+252)t=352t
这样我们就把两个单项式合并为一个单项式了,从而使运算变得更简便。
探究
1.填空:
(1)100t-252t=
(2)3x2+2x2=
(3)3ab2-4ab2=
(4)3kg+2kg=
(5)3km+2km=
(6)3kg+2km=
(100-252)t=-152t
5x2
-ab2
5kg
5km
小组讨论:从多项式的项的字母和相同字母的指数方面观察,上述前五个运算有什么共同特点,你能从中得出什么规律?
不难发现:观察(1)中多项式的项100t和-252t,它们含有相同的字母t,并且t的指数都是1;
(2)中多项式的项3x2和2x2,它们都含有相同的字母x,并且x的指数都是2;(3)中的多项式的项3ab2与-4ab2,它们都含有字母a,b,并且a都是一次,b都是二次;(4)中多项式的项3kg和2kg,它们都含有相同的字母k和g,并且k都是一次,g都是一次;(5)中多项式的项3km和2km,它们都含有相同的字母k和m,并且k都是一次,m都是一次;(6)中多项式的项3kg和2km,它们所含字母不完全相同,即字母因数不相同,不能相加
小组讨论:观察下列各单项式,看一看那些能够相加后变成一个单项式?
8x5y,-mn2,5a,-x5y,7mn2,9a,-3x5y,o,-3xy2,o.4mn2,5,2xy3
我们发现:8x5y,-x5y,-3x5y可以相加变成一个多项式;-mn2,7mn2,4mn2也可以相加变成一个多项式;还要5a与9a;以及0和5。
我们规定:像上述单项式这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项
同时规定:所有常数项都是同类项
例1.下列格式,是同类项的一组为( )
A. a2b与-ab2; B.xy6与-5y6x; C.5x与xy; D.5ab与6a2b
B
例2.若-3x2ym与0.75xny3是同类项,那么m=————,n=————
3
2
判断下列两项是否为同类项:
(1)-5ab3与3a3b
(2)3xy与3x
(3)-5m2n3与2n3m2
(4)53与35
(5)x3与53
不是
不是
是
是
不是
解决问题:邱粤买了3只笔芯和5个笔记本,已知笔芯每只a元,笔记本每本3a元,
请你帮邱粤算一下,她该付多少钱?
3a+5x3a=
3a+15a
=(3+15)a
=18a
不难发现:逆用乘法的分配律,保持同类项中的字母和字母的指数不
变,把系数相加,就能把几个同类项合并为一个单项式,从而使计算简便。
注意:只有同类项才能合并,并且不能遗漏;不是同类项不能合并
合并同类项:把多项式中的同类项合并为一项,称为合并同类项。
兄弟,你好呀!不认得哥啦?
我们不是一家的,不是的嘛
合并同类项的法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变,没有同类项的项,作为和的一个加数
小组讨论:怎样合并同类项?
合并同类项:4X2+2X+7+3X-8X2-2
哥,我在这儿
例:4x2 + 2x + 7 + 3x - 8x2 - 2
=4x2 - 8x2 + 2x + 3x + 7 - 2
=( 4x2 - 8x2)+ (2x + 3x)+ (7 – 2)
=(4- 8)x2 + (2 + 3)x + (7 – 2)
= -4 x2 + 5 x +5
②交换律
③结合律
④分配律
2.法则要点:
在合并同类项时结果往往是一个多项式,通常把这个结果写成按某一个字母的升幂或降幂的形式排列。
含有多个不同的同类项的多项式如何合并呢?
注意符号
①找同类项
⑤合并:
A.系数相加减;
B.字母和字母的指数不变。
= 5 + 5 x -4 x2
下列各题计算的结果对不对?如果不对,
指出错在哪里?
瞧一瞧:
×
√
×
√
练一练
注意符号
②交换律
③结合律
④分配律
①找同类项
⑤合并:
A.系数相加减;
B.字母和字母的指数不变。
养成好习惯
比一比,看谁算得快!
规则:同桌之间一个直接代入求值,另一个先合并同类项,再代入求值,看谁算得又快又对。
四. 巩固练习,拓展提高
1.下列各项不是同类项的是( )
A.-3x2y与2x2y B.-2xy2与3x2y C.-5x2y与3yx2 D.3mn2与2mn2
2.合并同类项正确的是( )
A.4a+b=5ab B.6xy2-6y2x=0
C.6x2-4x2=2 D.3x2+2x3=5x5
B
B
3.课堂练习:课本第66页练习第一题
4.例3.
(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,平均每小时上升0.5cm.这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正,第一天水位的变化量为-2acm,第二天的水位变化量为0.5cm.
两天水位的总变化量为 :-2a+0.5a
=(-2+0.5)a
=-1.5a
(2) 某商店原有5袋大米,每袋大米x千克,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?
解:把进货的数量记为正,售出的数量记为负,进货后这个商店共有大米
5x-3x+4x
=(5-3+4)x
=6x(千克)
五 课堂小结
通过这节课的学习你学到了什么?
同
类
项
相同字母的指数一样
所含字母一样
合并
法则
要点
②交换律
③结合律
④分配律
①找同类项
⑤合并:
A.系数相加减;
B.字母和字母的指数不变。
课后练习:
课本66页练习的2,3题
整式的加减
合并同类项
整式的加减
中学阶段是人生道路上的加油站
一.温故而知新
1.请任意写一个单项式,并写出这个单项式的系数和次数。
2.将同小组同学写出的单项式写在一起,就变成了一个新的式子,观察这个式子的组成可以分为哪两部分?
3.我们发现:无论怎么分,都是两个整式的和,今天,我们一起来研究有关整式的和的问题。
252t
在青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段,根据下表提供的信息你能算出各段的铁路及这段铁路的全长吗?
二:探究新知
速度
(千米/时) 时间
(小时) 路程(千米)
冻土段 100 t
非冻土地段 120 2.1t
铁路全长
100t
+
能化简吗?依据是什么?
单项式
单项式
整式
整式
+
还记得乘法分配律吗?用字母如何表示?
一个数与几个数的和相乘,等于这个数与和的每个加数的积的和。
用字母可以表示为
a(b+c)=ab+ac
如果把这个等式两边交换位置就变成了
ab+ac= a(b+c)
探究
(1)计算
100x2+252x2=———
100x(-2)+252X(-2)=———
(2)观察式子:100t+252t,分析它的构成与(1)中两个算式有何异同?
相同点:都形如ba+ca,在每个算式里都有相同因数
不同点:(1)中相同因数都是数字因数,(2)中相同因数是字母因数
想一想:能否应用等式ab+ac=a(b+c)来对式子100t+252t化简呢?为什么?
学习上节课 阅读与思考 栏目时,我们已经知道:随着实践的发展,代数学的基础使用字母表示数,它首要研究的就是用字母表示的式子的运算法则和方程的解法
我们知道:字母虽然不是具体的数,但是它可以表示各种各样的数,包括整式,那么化简100t+252t就不是一件困难的事情了
100t+252t=(100+252)t=352t
这样我们就把两个单项式合并为一个单项式了,从而使运算变得更简便。
探究
1.填空:
(1)100t-252t=
(2)3x2+2x2=
(3)3ab2-4ab2=
(4)3kg+2kg=
(5)3km+2km=
(6)3kg+2km=
(100-252)t=-152t
5x2
-ab2
5kg
5km
小组讨论:从多项式的项的字母和相同字母的指数方面观察,上述前五个运算有什么共同特点,你能从中得出什么规律?
不难发现:观察(1)中多项式的项100t和-252t,它们含有相同的字母t,并且t的指数都是1;
(2)中多项式的项3x2和2x2,它们都含有相同的字母x,并且x的指数都是2;(3)中的多项式的项3ab2与-4ab2,它们都含有字母a,b,并且a都是一次,b都是二次;(4)中多项式的项3kg和2kg,它们都含有相同的字母k和g,并且k都是一次,g都是一次;(5)中多项式的项3km和2km,它们都含有相同的字母k和m,并且k都是一次,m都是一次;(6)中多项式的项3kg和2km,它们所含字母不完全相同,即字母因数不相同,不能相加
小组讨论:观察下列各单项式,看一看那些能够相加后变成一个单项式?
8x5y,-mn2,5a,-x5y,7mn2,9a,-3x5y,o,-3xy2,o.4mn2,5,2xy3
我们发现:8x5y,-x5y,-3x5y可以相加变成一个多项式;-mn2,7mn2,4mn2也可以相加变成一个多项式;还要5a与9a;以及0和5。
我们规定:像上述单项式这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项
同时规定:所有常数项都是同类项
例1.下列格式,是同类项的一组为( )
A. a2b与-ab2; B.xy6与-5y6x; C.5x与xy; D.5ab与6a2b
B
例2.若-3x2ym与0.75xny3是同类项,那么m=————,n=————
3
2
判断下列两项是否为同类项:
(1)-5ab3与3a3b
(2)3xy与3x
(3)-5m2n3与2n3m2
(4)53与35
(5)x3与53
不是
不是
是
是
不是
解决问题:邱粤买了3只笔芯和5个笔记本,已知笔芯每只a元,笔记本每本3a元,
请你帮邱粤算一下,她该付多少钱?
3a+5x3a=
3a+15a
=(3+15)a
=18a
不难发现:逆用乘法的分配律,保持同类项中的字母和字母的指数不
变,把系数相加,就能把几个同类项合并为一个单项式,从而使计算简便。
注意:只有同类项才能合并,并且不能遗漏;不是同类项不能合并
合并同类项:把多项式中的同类项合并为一项,称为合并同类项。
兄弟,你好呀!不认得哥啦?
我们不是一家的,不是的嘛
合并同类项的法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变,没有同类项的项,作为和的一个加数
小组讨论:怎样合并同类项?
合并同类项:4X2+2X+7+3X-8X2-2
哥,我在这儿
例:4x2 + 2x + 7 + 3x - 8x2 - 2
=4x2 - 8x2 + 2x + 3x + 7 - 2
=( 4x2 - 8x2)+ (2x + 3x)+ (7 – 2)
=(4- 8)x2 + (2 + 3)x + (7 – 2)
= -4 x2 + 5 x +5
②交换律
③结合律
④分配律
2.法则要点:
在合并同类项时结果往往是一个多项式,通常把这个结果写成按某一个字母的升幂或降幂的形式排列。
含有多个不同的同类项的多项式如何合并呢?
注意符号
①找同类项
⑤合并:
A.系数相加减;
B.字母和字母的指数不变。
= 5 + 5 x -4 x2
下列各题计算的结果对不对?如果不对,
指出错在哪里?
瞧一瞧:
×
√
×
√
练一练
注意符号
②交换律
③结合律
④分配律
①找同类项
⑤合并:
A.系数相加减;
B.字母和字母的指数不变。
养成好习惯
比一比,看谁算得快!
规则:同桌之间一个直接代入求值,另一个先合并同类项,再代入求值,看谁算得又快又对。
四. 巩固练习,拓展提高
1.下列各项不是同类项的是( )
A.-3x2y与2x2y B.-2xy2与3x2y C.-5x2y与3yx2 D.3mn2与2mn2
2.合并同类项正确的是( )
A.4a+b=5ab B.6xy2-6y2x=0
C.6x2-4x2=2 D.3x2+2x3=5x5
B
B
3.课堂练习:课本第66页练习第一题
4.例3.
(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,平均每小时上升0.5cm.这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正,第一天水位的变化量为-2acm,第二天的水位变化量为0.5cm.
两天水位的总变化量为 :-2a+0.5a
=(-2+0.5)a
=-1.5a
(2) 某商店原有5袋大米,每袋大米x千克,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?
解:把进货的数量记为正,售出的数量记为负,进货后这个商店共有大米
5x-3x+4x
=(5-3+4)x
=6x(千克)
五 课堂小结
通过这节课的学习你学到了什么?
同
类
项
相同字母的指数一样
所含字母一样
合并
法则
要点
②交换律
③结合律
④分配律
①找同类项
⑤合并:
A.系数相加减;
B.字母和字母的指数不变。
课后练习:
课本66页练习的2,3题
