人教版八年级上册:14.2.1 平方差公式 课件(22张PPT)
文档属性
| 名称 | 人教版八年级上册:14.2.1 平方差公式 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 876.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 20:52:09 | ||
图片预览



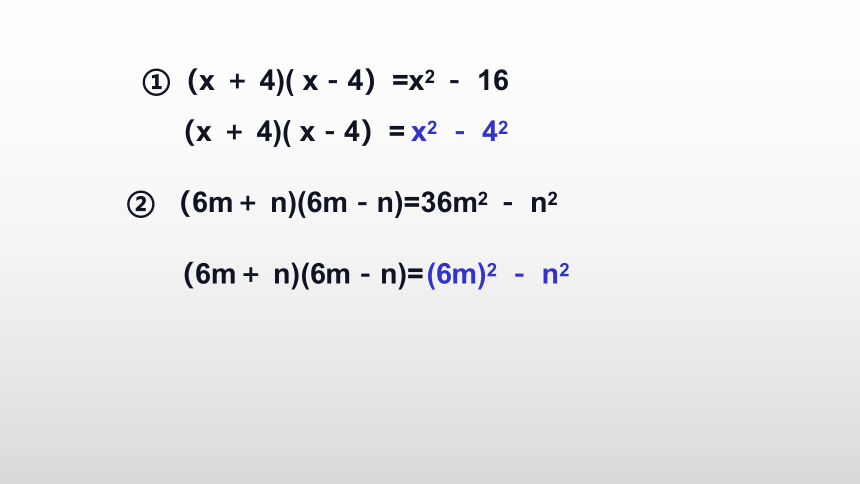



文档简介
给我最大快乐的,不是已懂的知识,
而是不断的学习.----高斯
14.2.1 平方差公式
多项式与多项式是如何相乘的?
(a+b)(m+n)
=am
+an
+bm
+bn
用一个多项式的每一项
乘另一个多项式的每一项
再把所得的积相加。
多项式乘法
法则是:
复习引入
①(x + 4)( x-4)
② (6m+ n)(6m-n)
计算下列各题
算一算,比一比,看谁算得又快又准
①(x + 4)( x-4)=x2 - 16
x2 - 42
(6m)2 - n2
(x + 4)( x-4)=
(6m+ n)(6m-n)=
② (6m+ n)(6m-n)=36m2 - n2
x2 - 42
(x + 4)( x-4)=
(6m)2 - n2
(6m+ n)(6m-n)=
它们的结果有什么特点?
等号的左边:两个数的和与差的积,
等号的右边:是这两个数的平方差.
观察计算结果, 你又发现了什么规律?
2、猜想:(a + b)(a- b)=——————.
(a+b)(a-b)
3证明:(1)代数
角度
(a + b)(a- b)=a2-b2.
∴(a + b)(a- b)=a2-b2.
(多项式乘法法则)
(合并同类项)
`
a
a
b
a2
b2
-
b
a
a
b
(a + b) (a - b)
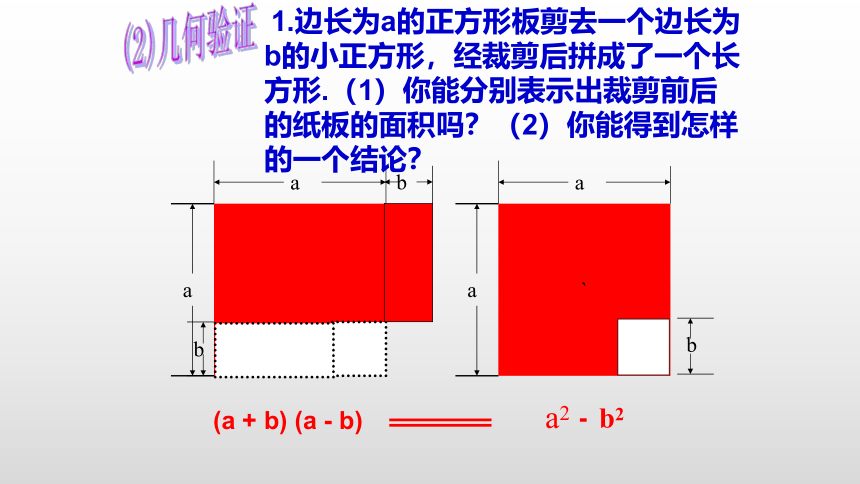
1.边长为a的正方形板剪去一个边长为b的小正方形,经裁剪后拼成了一个长方形.(1)你能分别表示出裁剪前后的纸板的面积吗?(2)你能得到怎样的一个结论?
(2)几何验证
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
公式变形:
1、(a – b ) ( a + b) = a2 - b2
2、(b + a )( -b + a ) = a2 - b2
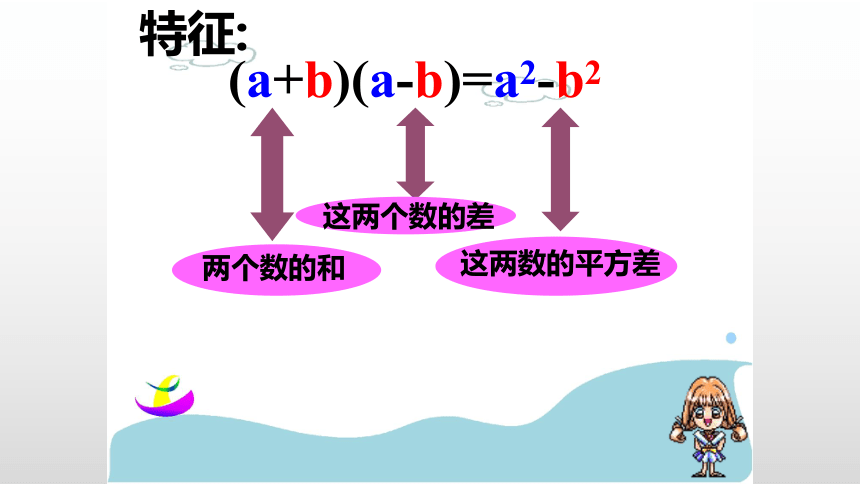
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
填表
(a+b)(a-b)
a
(相同)
b
(相反)
a2-b2
(平方差)
最后结果
(2x+2)(2x-2)
(m+3n)(3n-m)
(-a+4b)(-a-4b)
2x
3n
-a
m
4b
(3n)2-m2
(-a)2- (4b)2
4x2-4
a2-16b2
9n2-m2
2
(2x)2-22
1、判断下列式子是否可用平方差公式。
(1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7 (-4k3+3y2)(-4k3-3y2)
是
否
是
是
是
是
否
例1:运用平方差公式计算:
(1)
(2)
(-x+3y)(x+3y)
(3x+2)( 3x-2 )
解: (3x+2)(3x-2)
(a+ b) ( a- b)
= a2 - b2
=(3x)2-22
= 9x2-4
解: (-x+3y)(x+3y)
=(3y-x)(3y+x)
= (3y)2-x2
= 9y2-x2
小明的计算正确吗?如果不正确应怎样改正?
(1) (-3a-2)(3a-2)
= 9a2 - 4
(2) ( x-y)( x+y)
= x2 – y2
2
3
2
3
2
3
解:
改正:
解:
(1) (-3a-2)(3a-2)
(2) ( x-y)( x+y)
=( x)2 – y2
= x2 - y2
2
3
2
3
2
3
4
9
( )
( )
= (-2-3a)(-2+3a)
= (-2)2 - (3a)2
= 4 - 9a2
【例2】计算
(1) 102×98. (2)(y+2)(y-2)-(y -1)(y+5).
【解析】
(1) 102×98
=(100+2)(100-2)
=1002-22
=10 000-4
=9 996.
(2)原式
=(y2-22)-(y2+5y-y-5)
= y2-22-y2-5y+y+5
=-4y+1.
练习、运用平方差公式计算:
(1)49×51 (2)9.8×10.2
独立思考 归纳验证
(1)公式左边两个二项式必须是
相同两数的和与差的积.
且左边两括号内的第一项相等、
第二项符号相反.
特征
结构
{
(2)公式右边是这两个数的平方差;
即左边括号内的第一项的平方
减去第二项的平方.
(3)公式中的 和 可以代表数,
也可以是代数式.
1.下列运算中正确的是( )
A. B.
C. D.
【解析】选B. 在A中3a+2a=5a;C中 ;
D中 .
2.已知a-b=1,则a2-b2-2b的值为( )
A.4 B.3 C.1 D.0
【解析】选C.a2-b2-2b=(a-b)(a+b)-2b=a+b-2b=a-b=1.
3.运用平方差公式计算.
(a+3b) (a-3b);
(2) (-3-2a) (-3 + 2a) ;
(3) 51×49;
而是不断的学习.----高斯
14.2.1 平方差公式
多项式与多项式是如何相乘的?
(a+b)(m+n)
=am
+an
+bm
+bn
用一个多项式的每一项
乘另一个多项式的每一项
再把所得的积相加。
多项式乘法
法则是:
复习引入
①(x + 4)( x-4)
② (6m+ n)(6m-n)
计算下列各题
算一算,比一比,看谁算得又快又准
①(x + 4)( x-4)=x2 - 16
x2 - 42
(6m)2 - n2
(x + 4)( x-4)=
(6m+ n)(6m-n)=
② (6m+ n)(6m-n)=36m2 - n2
x2 - 42
(x + 4)( x-4)=
(6m)2 - n2
(6m+ n)(6m-n)=
它们的结果有什么特点?
等号的左边:两个数的和与差的积,
等号的右边:是这两个数的平方差.
观察计算结果, 你又发现了什么规律?
2、猜想:(a + b)(a- b)=——————.
(a+b)(a-b)
3证明:(1)代数
角度
(a + b)(a- b)=a2-b2.
∴(a + b)(a- b)=a2-b2.
(多项式乘法法则)
(合并同类项)
`
a
a
b
a2
b2
-
b
a
a
b
(a + b) (a - b)
1.边长为a的正方形板剪去一个边长为b的小正方形,经裁剪后拼成了一个长方形.(1)你能分别表示出裁剪前后的纸板的面积吗?(2)你能得到怎样的一个结论?
(2)几何验证
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
公式变形:
1、(a – b ) ( a + b) = a2 - b2
2、(b + a )( -b + a ) = a2 - b2
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
填表
(a+b)(a-b)
a
(相同)
b
(相反)
a2-b2
(平方差)
最后结果
(2x+2)(2x-2)
(m+3n)(3n-m)
(-a+4b)(-a-4b)
2x
3n
-a
m
4b
(3n)2-m2
(-a)2- (4b)2
4x2-4
a2-16b2
9n2-m2
2
(2x)2-22
1、判断下列式子是否可用平方差公式。
(1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7 (-4k3+3y2)(-4k3-3y2)
是
否
是
是
是
是
否
例1:运用平方差公式计算:
(1)
(2)
(-x+3y)(x+3y)
(3x+2)( 3x-2 )
解: (3x+2)(3x-2)
(a+ b) ( a- b)
= a2 - b2
=(3x)2-22
= 9x2-4
解: (-x+3y)(x+3y)
=(3y-x)(3y+x)
= (3y)2-x2
= 9y2-x2
小明的计算正确吗?如果不正确应怎样改正?
(1) (-3a-2)(3a-2)
= 9a2 - 4
(2) ( x-y)( x+y)
= x2 – y2
2
3
2
3
2
3
解:
改正:
解:
(1) (-3a-2)(3a-2)
(2) ( x-y)( x+y)
=( x)2 – y2
= x2 - y2
2
3
2
3
2
3
4
9
( )
( )
= (-2-3a)(-2+3a)
= (-2)2 - (3a)2
= 4 - 9a2
【例2】计算
(1) 102×98. (2)(y+2)(y-2)-(y -1)(y+5).
【解析】
(1) 102×98
=(100+2)(100-2)
=1002-22
=10 000-4
=9 996.
(2)原式
=(y2-22)-(y2+5y-y-5)
= y2-22-y2-5y+y+5
=-4y+1.
练习、运用平方差公式计算:
(1)49×51 (2)9.8×10.2
独立思考 归纳验证
(1)公式左边两个二项式必须是
相同两数的和与差的积.
且左边两括号内的第一项相等、
第二项符号相反.
特征
结构
{
(2)公式右边是这两个数的平方差;
即左边括号内的第一项的平方
减去第二项的平方.
(3)公式中的 和 可以代表数,
也可以是代数式.
1.下列运算中正确的是( )
A. B.
C. D.
【解析】选B. 在A中3a+2a=5a;C中 ;
D中 .
2.已知a-b=1,则a2-b2-2b的值为( )
A.4 B.3 C.1 D.0
【解析】选C.a2-b2-2b=(a-b)(a+b)-2b=a+b-2b=a-b=1.
3.运用平方差公式计算.
(a+3b) (a-3b);
(2) (-3-2a) (-3 + 2a) ;
(3) 51×49;
