人教版八年级数学上册教学13.4 课题学习 最短路径问题课件(18张)
文档属性
| 名称 | 人教版八年级数学上册教学13.4 课题学习 最短路径问题课件(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 777.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 00:00:00 | ||
图片预览






文档简介
---13.4课题学习 最短路径问题1
B
A
l
人教版数学八年级上册
将军饮马问题
学习目标
1.能利用轴对称变换解决实际问题.
2.能利用作图解决生活中的轴对称问题. (作图建模)
路径极值问题的转换方法.
学习重点:
B
·
l
A
·
如图所示,点A、B分别是直线 l异侧的两个点,如何在 l 上找到一个点,使得这个点到点A,点B的距离的和最短?
两点之间,线段最短.
连接AB,与直线 l相交于一点,这个交点即为所求.
复习旧知
问题1 如图,牧马人从A 地出发,到一条笔直的河边 l 饮马,然后到B 地。牧马人到河边的什么地方饮马,可使所走的路径最短?
解题思路
1、解读题干,提取信息
A地、B地抽象为两个点,笔直河边抽象为直线 l ,在河边什么地方饮马抽象为直线 l上一个动点C,这样就将问题转化为数学模型:
B
·
·
A
l
已知:点A、B在直线 l 的同侧,
求作:在直线 l 上找一个点C,使AC+BC最小。
解题思路
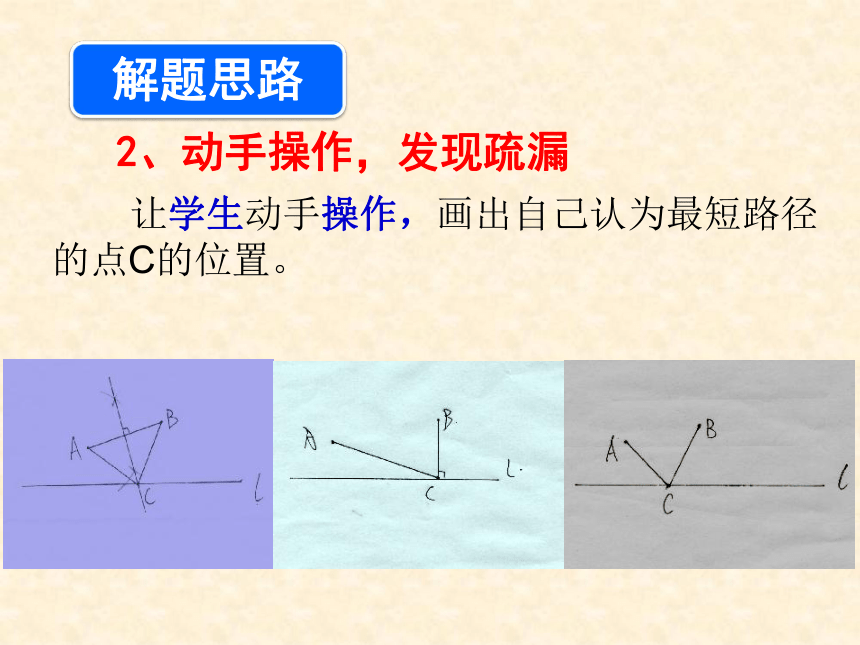
让学生动手操作,画出自己认为最短路径的点C的位置。
2、动手操作,发现疏漏
解题思路
(1)探究点A、B在直线 l 的异侧,在直线 l 上找一点C,使AC+BC最小。
l
A
B
3、探究问题,突破难点
解题思路
只要连接这两点,与直线的交点即为所求.
(2)探究点A、B在直线 l 的同侧,在直线 l 上找一点C,使AC+BC最小。
l
A
B
3、探究问题,突破难点
解题思路
l
A
B
C
B′
轴对称
转化
方法小结
线段的和最短
一条线段
B
·
l
A
·
B′
4、规范作图,学会方法
(1)作出点B关于 直线 l 的对称点B′ ,利用轴对称的性质可以得到CB′=CB.
·
解题思路
(2)连接AB′,交直线 l 于点C.
则点C 即为所求.
B
·
l
A
·
B′
C
4、规范作图,学会方法
解题思路
5、推理论证,证明结论
证明:在直线 l 上另取一点C′,连接AC′,B′C′,BC′.
根据轴对称的性质可知BC=B′C,BC′=B′C′
∴AC+BC=AC+B′C=AB′
AC′+BC′=AC′+B′C′
由△AB′C′三边关系可知
A′B 则AC+BC ∴AC+BC最短
B
·
l
A
·
B′
C
C′
解题思路
l
A
B
C
l
A
B
C
B′
转化
数学建模
轴对称
变换
思想方法
如图,A、B是两个蓄水池,都在河流 a 的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹).
解:如图,P点即为该点.
变式1---变背景
牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
A?
B?
P
Q
.
.
.
.
变式2---变任务
l1
l2
A
A2
A1
M
N
要在两条街道 l1和 l2上各设立一个邮筒,A处是邮局,问邮筒设在哪里才能使邮递员从邮局出发,到两个邮筒取完信再回到邮局的路程最短?
变式3---变地点
P
拓展---中考题
(△PAC周长最小时,求点P的坐标。)
(2017·七里河) 如图,抛物线y=ax2+bx+c 经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
B
A
l
人教版数学八年级上册
将军饮马问题
学习目标
1.能利用轴对称变换解决实际问题.
2.能利用作图解决生活中的轴对称问题. (作图建模)
路径极值问题的转换方法.
学习重点:
B
·
l
A
·
如图所示,点A、B分别是直线 l异侧的两个点,如何在 l 上找到一个点,使得这个点到点A,点B的距离的和最短?
两点之间,线段最短.
连接AB,与直线 l相交于一点,这个交点即为所求.
复习旧知
问题1 如图,牧马人从A 地出发,到一条笔直的河边 l 饮马,然后到B 地。牧马人到河边的什么地方饮马,可使所走的路径最短?
解题思路
1、解读题干,提取信息
A地、B地抽象为两个点,笔直河边抽象为直线 l ,在河边什么地方饮马抽象为直线 l上一个动点C,这样就将问题转化为数学模型:
B
·
·
A
l
已知:点A、B在直线 l 的同侧,
求作:在直线 l 上找一个点C,使AC+BC最小。
解题思路
让学生动手操作,画出自己认为最短路径的点C的位置。
2、动手操作,发现疏漏
解题思路
(1)探究点A、B在直线 l 的异侧,在直线 l 上找一点C,使AC+BC最小。
l
A
B
3、探究问题,突破难点
解题思路
只要连接这两点,与直线的交点即为所求.
(2)探究点A、B在直线 l 的同侧,在直线 l 上找一点C,使AC+BC最小。
l
A
B
3、探究问题,突破难点
解题思路
l
A
B
C
B′
轴对称
转化
方法小结
线段的和最短
一条线段
B
·
l
A
·
B′
4、规范作图,学会方法
(1)作出点B关于 直线 l 的对称点B′ ,利用轴对称的性质可以得到CB′=CB.
·
解题思路
(2)连接AB′,交直线 l 于点C.
则点C 即为所求.
B
·
l
A
·
B′
C
4、规范作图,学会方法
解题思路
5、推理论证,证明结论
证明:在直线 l 上另取一点C′,连接AC′,B′C′,BC′.
根据轴对称的性质可知BC=B′C,BC′=B′C′
∴AC+BC=AC+B′C=AB′
AC′+BC′=AC′+B′C′
由△AB′C′三边关系可知
A′B
B
·
l
A
·
B′
C
C′
解题思路
l
A
B
C
l
A
B
C
B′
转化
数学建模
轴对称
变换
思想方法
如图,A、B是两个蓄水池,都在河流 a 的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹).
解:如图,P点即为该点.
变式1---变背景
牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
A?
B?
P
Q
.
.
.
.
变式2---变任务
l1
l2
A
A2
A1
M
N
要在两条街道 l1和 l2上各设立一个邮筒,A处是邮局,问邮筒设在哪里才能使邮递员从邮局出发,到两个邮筒取完信再回到邮局的路程最短?
变式3---变地点
P
拓展---中考题
(△PAC周长最小时,求点P的坐标。)
(2017·七里河) 如图,抛物线y=ax2+bx+c 经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
