人教版七年级数学上册3.1.2等式的性质课件(共30张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.1.2等式的性质课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 20:10:24 | ||
图片预览







文档简介
课前寄语
好的习惯是一笔财富,一旦你拥有它,你就会受益终身。
——美国
比尔盖茨
复习回顾
1、什么是方程?
什么是一元一次方程?
2、估算下列方程的解:
3.1.2等式的性质
1、理解等式的概念,掌握等式的性质。
2、熟练运用等式的性质解一元一次方程。
3、通过观察、探究、归纳、应用等活动,体会化归思想。
学习目标
1、用什么符号连接的式子是等式?
自学提示
2、等式的性质内容是什么?课本上是怎么探索、验证的?你会用字母表示等式的性质吗?
3、如何运用等式的性质解方程?你会验证方程的解吗?
牛刀小试
下列式子中是等式的有:
用等号表示相等关系的式子,叫等式。
4
>
3
2x≠2
3x2+2xy
1、
2、
3、
4、
5、
6、
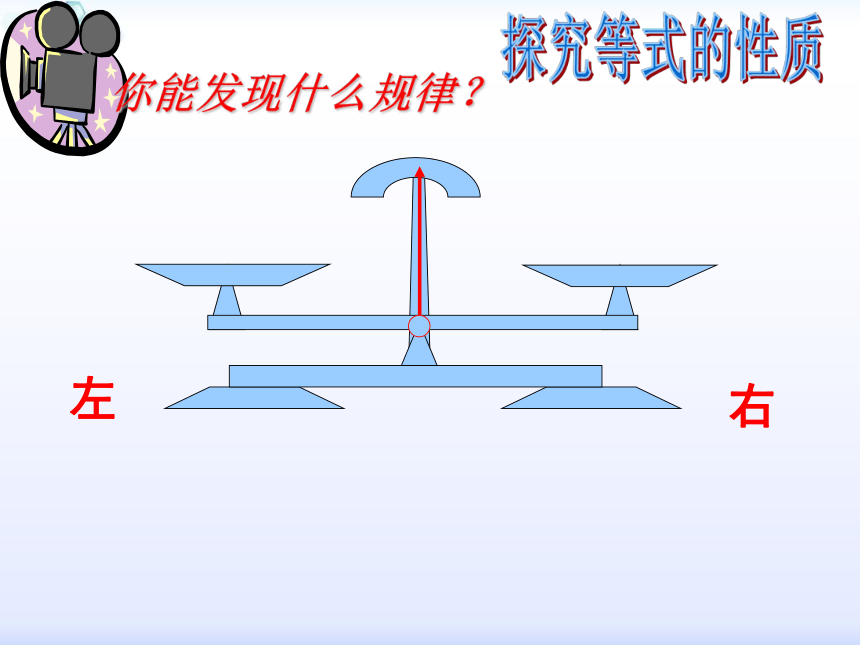
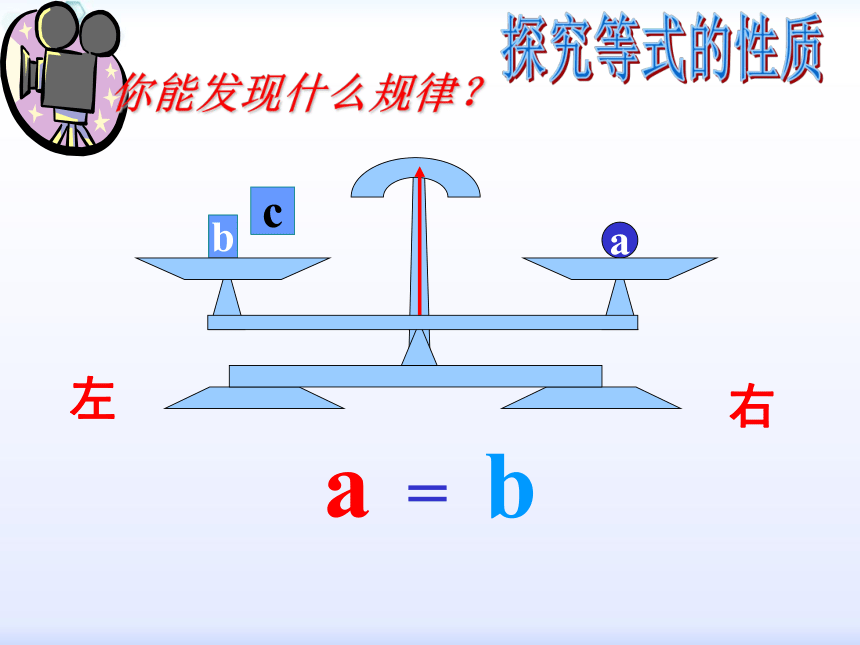
你能发现什么规律?
右
左
探究等式的性质
a
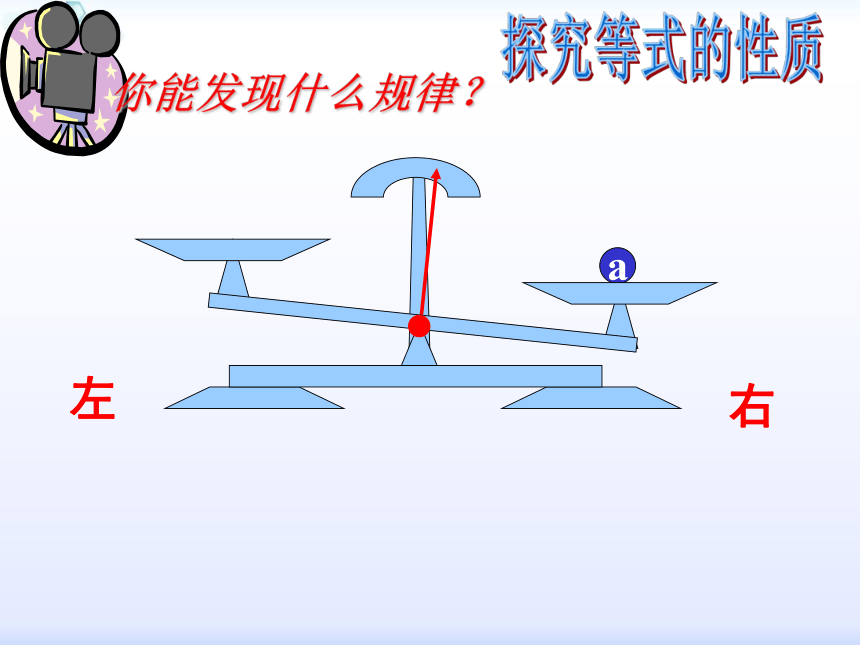
你能发现什么规律?
右
左
探究等式的性质
a
b
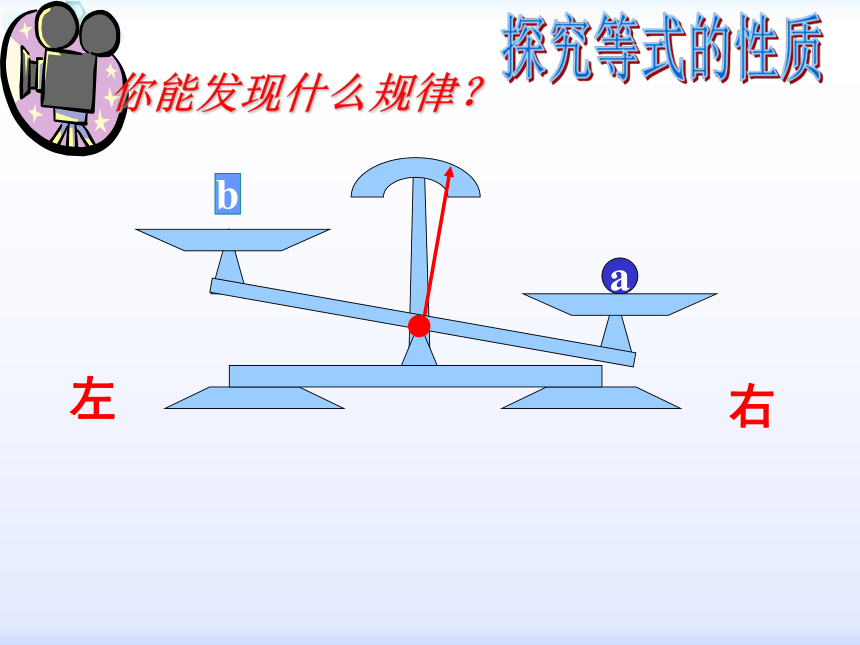
你能发现什么规律?
右
左
探究等式的性质
b
a
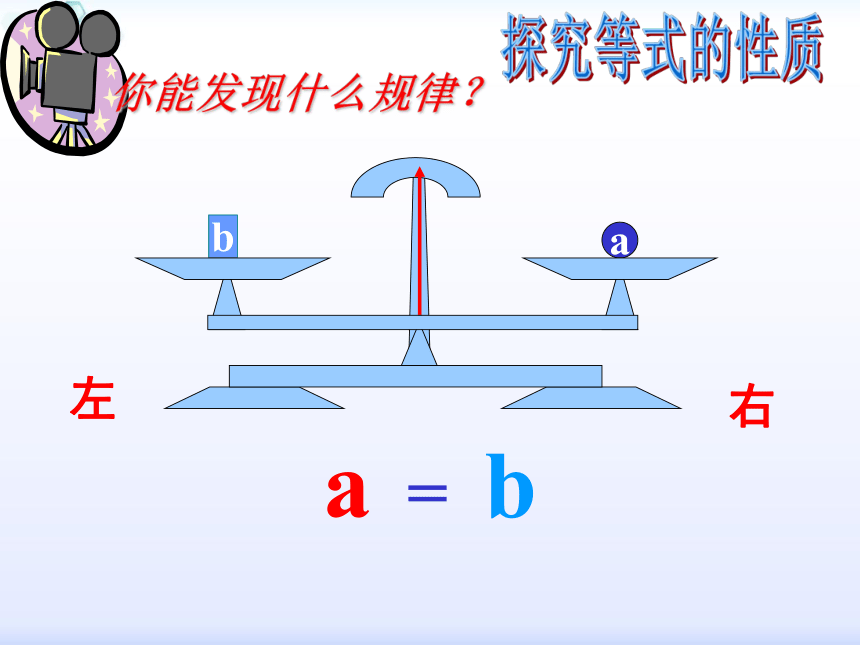
你能发现什么规律?
a
=
b
右
左
探究等式的性质
b
a
你能发现什么规律?
a
=
b
c
右
左
探究等式的性质
a
c
b
你能发现什么规律?
a
=
b
右
左
探究等式的性质
c
b
c
a
你能发现什么规律?
a
=
b
a+c
b+c
=
右
左
探究等式的性质
c
c
你能发现什么规律?
a
=
b
a
b
右
左
探究等式的性质
c
你能发现什么规律?
a
=
b
a
b
右
左
探究等式的性质
你能发现什么规律?
a
=
b
a-c
b-c
=
b
a
右
左
探究等式的性质
归纳
等式的性质1:
等式两边同加(或同减)同一个数(或式子),结果仍相等。
如果a=b,那么a+c=b+c
b
a
你能发现什么规律?
a
=
b
右
左
探究等式的性质
b
a
你能发现什么规律?
a
=
b
右
左
a
b
2a
=
2b
探究等式的性质
b
a
你能发现什么规律?
a
=
b
右
左
b
b
a
a
3a
=
3b
探究等式的性质
b
a
你能发现什么规律?
a
=
b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac
=
bc
探究等式的性质
÷3
÷3
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍是等式
如果 ,那么
b
a
=
如果 ,那么
b
a
=
你能发现什么规律?
探究等式的性质
练习1.
用适当的数或式子填空,使结果仍是等式。
(1)若
4x
=
7x
–
5
则
4x
+
=
7x
(2)
若
3a
+
4
=
8
则
3a
=
8
+
.
提示:
1、观察等式变形前后两边各有什么变化
2、应怎么变化可使等式依然相等
关键:同侧对比
注意符号
应用等式的性质
练习2.
用适当的数或式子填空,使结果仍是等式。
关键:
同侧对比
注意符号
(1)
3x
=
-
9
(2)
-
0.5x
=
2
(3)
2x
+
1
=
3
两边都____
两边都____
得 x
=
____
得 x
=
____
两边都_____
两边都__
得 2x
=______
得x
=
_______
应用等式的性质
例题
用等式的性质解方程
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
怎样检验?
1、填空,并在括号内注明利用了等式的哪条性质。
(1)如果5+x=4,那么x=____(
)
(2)如果-2x=6,那么x=____
(
)
(3)
如果9x+4=5x,那么4x=____(
)
(4)
如果0.2x=10,那么x=____.(
)
达标检测
练习2:用等式的性质解下列方程并检验:
(1)x-5=6;
(2)0.3x=45;
(3)5x+4=0;
(4)2
-
x
=
3.
挑战自我
记住了
?
【等式性质
2】
【等式性质1】
课堂小结
1.通过今天的学习,你掌握了哪些知识点?
2.通过今天的学习,你学会了哪些解题方法?
利用等式的性质解以x为未知数的方程,就是把方程逐步转化为x=a(a是常数)的形式
数学书83页
习题3.1
第4,5,6题
同步练习册40页
选做题
用等式的性质求下列方程的解
(1)-5x=5-6x
(2)
-3=5y+2
(3)
7y-6=3y
布置作业
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量。
——??高尔基
好的习惯是一笔财富,一旦你拥有它,你就会受益终身。
——美国
比尔盖茨
复习回顾
1、什么是方程?
什么是一元一次方程?
2、估算下列方程的解:
3.1.2等式的性质
1、理解等式的概念,掌握等式的性质。
2、熟练运用等式的性质解一元一次方程。
3、通过观察、探究、归纳、应用等活动,体会化归思想。
学习目标
1、用什么符号连接的式子是等式?
自学提示
2、等式的性质内容是什么?课本上是怎么探索、验证的?你会用字母表示等式的性质吗?
3、如何运用等式的性质解方程?你会验证方程的解吗?
牛刀小试
下列式子中是等式的有:
用等号表示相等关系的式子,叫等式。
4
>
3
2x≠2
3x2+2xy
1、
2、
3、
4、
5、
6、
你能发现什么规律?
右
左
探究等式的性质
a
你能发现什么规律?
右
左
探究等式的性质
a
b
你能发现什么规律?
右
左
探究等式的性质
b
a
你能发现什么规律?
a
=
b
右
左
探究等式的性质
b
a
你能发现什么规律?
a
=
b
c
右
左
探究等式的性质
a
c
b
你能发现什么规律?
a
=
b
右
左
探究等式的性质
c
b
c
a
你能发现什么规律?
a
=
b
a+c
b+c
=
右
左
探究等式的性质
c
c
你能发现什么规律?
a
=
b
a
b
右
左
探究等式的性质
c
你能发现什么规律?
a
=
b
a
b
右
左
探究等式的性质
你能发现什么规律?
a
=
b
a-c
b-c
=
b
a
右
左
探究等式的性质
归纳
等式的性质1:
等式两边同加(或同减)同一个数(或式子),结果仍相等。
如果a=b,那么a+c=b+c
b
a
你能发现什么规律?
a
=
b
右
左
探究等式的性质
b
a
你能发现什么规律?
a
=
b
右
左
a
b
2a
=
2b
探究等式的性质
b
a
你能发现什么规律?
a
=
b
右
左
b
b
a
a
3a
=
3b
探究等式的性质
b
a
你能发现什么规律?
a
=
b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac
=
bc
探究等式的性质
÷3
÷3
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍是等式
如果 ,那么
b
a
=
如果 ,那么
b
a
=
你能发现什么规律?
探究等式的性质
练习1.
用适当的数或式子填空,使结果仍是等式。
(1)若
4x
=
7x
–
5
则
4x
+
=
7x
(2)
若
3a
+
4
=
8
则
3a
=
8
+
.
提示:
1、观察等式变形前后两边各有什么变化
2、应怎么变化可使等式依然相等
关键:同侧对比
注意符号
应用等式的性质
练习2.
用适当的数或式子填空,使结果仍是等式。
关键:
同侧对比
注意符号
(1)
3x
=
-
9
(2)
-
0.5x
=
2
(3)
2x
+
1
=
3
两边都____
两边都____
得 x
=
____
得 x
=
____
两边都_____
两边都__
得 2x
=______
得x
=
_______
应用等式的性质
例题
用等式的性质解方程
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
怎样检验?
1、填空,并在括号内注明利用了等式的哪条性质。
(1)如果5+x=4,那么x=____(
)
(2)如果-2x=6,那么x=____
(
)
(3)
如果9x+4=5x,那么4x=____(
)
(4)
如果0.2x=10,那么x=____.(
)
达标检测
练习2:用等式的性质解下列方程并检验:
(1)x-5=6;
(2)0.3x=45;
(3)5x+4=0;
(4)2
-
x
=
3.
挑战自我
记住了
?
【等式性质
2】
【等式性质1】
课堂小结
1.通过今天的学习,你掌握了哪些知识点?
2.通过今天的学习,你学会了哪些解题方法?
利用等式的性质解以x为未知数的方程,就是把方程逐步转化为x=a(a是常数)的形式
数学书83页
习题3.1
第4,5,6题
同步练习册40页
选做题
用等式的性质求下列方程的解
(1)-5x=5-6x
(2)
-3=5y+2
(3)
7y-6=3y
布置作业
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量。
——??高尔基
