人教版七年级上册3.4 实际问题与一元一次方程第一课时 配套问题与工程问题课件(21张)
文档属性
| 名称 | 人教版七年级上册3.4 实际问题与一元一次方程第一课时 配套问题与工程问题课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 11:40:46 | ||
图片预览








文档简介
3.4 实际问题与一元一次方程
第一课时 配套问题与工程问题
第三章 一元一次方程
学习目标
学习目标
1.会通过列方程解决“配套问题”和“工程问题”;
2.掌握列方程解决实际问题的一般步骤;
3.通过列方程解决实际问题的过程,体会建模思想。
重点
建立模型解决实际问题的一般方法。
难点
列方程解决“配套问题”和“工程问题”。
课前回顾(解一元一次方程的步骤及注意事项)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}步骤
具体做法
依据
注意事项
去分母
在方程两边都乘以各分母的最小公倍数
等式
性质2
不要漏乘不含分母的项
去括号
一般先去小括号,再去中括号,最后去大括号
分配律 去括号法则
不要漏乘括号中的每一项
移项
把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号
移项法则
1)移动的项一定要变号,
不移的项不变号
2)注意项较多时不要漏项
合并同类项
把方程变为ax=b
(a≠0 ) 的最简形式
合并同类项法则
1)把系数相加
2)字母和字母的指数不变
系数化为1
等式性质2
解的分子,分母位置不要颠倒
生活中,有很多需要进行配套的问题,比如我们使用的餐桌需要和椅子进行配套,你能举出生活中一些配套的问题吗?
情境导入
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
二、应用与探究
?思考 与分析
(1)请你一边阅读题目,一边画出文段中的关键信息,并用自己的语言概括出来.
“每天生产的螺钉和螺母刚好配套”如何用数学语言表示?
“1个螺钉要配2个螺母”
“螺母的总产量=螺钉总产量的2 倍”
列表分析:
产品类型
生产人数
每人产量
总产量
螺钉
螺母
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
22﹣x
螺母总产量是螺钉的2倍
1 200
2 000
x
每人每天的工作效率×人数=每天的工作量(产品数量)
由“螺母的总产量=螺钉总产量的2 倍”可得方程
?
例题解析
解:设应安排 x 名工人生产螺钉,________名工人生产螺母,由题意得
2×1 200 x = 2 000 ( 22 - x).
去括号,得
2 400 x = 44 000 – 2 000 x.
移项,合并同类项,得
4 400 x = 44 000.
x = 10.
生产螺母的人数为
22 – x = 12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
(22 – x)
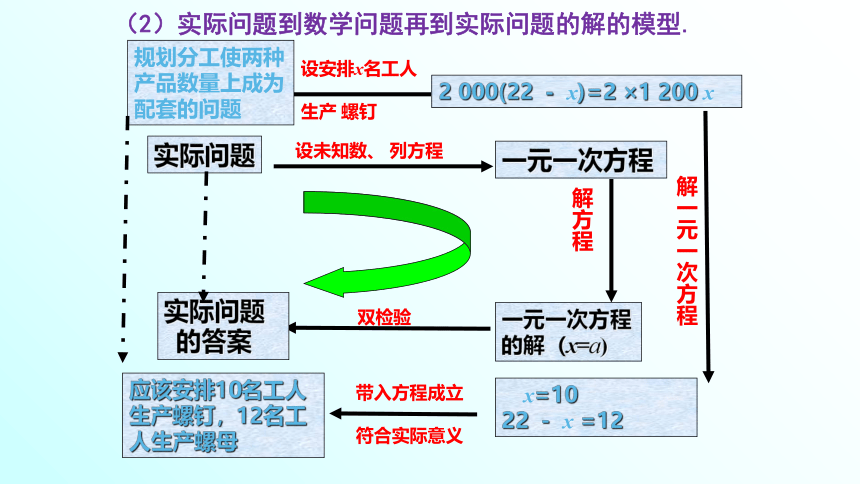
实际问题
设安排x名工人
生产 螺钉
解方程
一元一次方程的解(x=a)
双检验
实际问题
的答案
规划分工使两种产品数量上成为配套的问题
设未知数、 列方程
一元一次方程
带入方程成立
符合实际意义
2 000(22 - x)=2 ×1 200 x
x=10
22 - x =12
解一元一次方程
应该安排10名工人生产螺钉,12名工人生产螺母
(2)实际问题到数学问题再到实际问题的解的模型.
例2.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
分析:
设这个班有x名学生.每人分3本,共分出3x本,加上剩余的20本,这批书共 ____ 本;每人分4本,需要___本,减去缺的25本,这批书共______本.
这批书的总数是一个定值,表示它的两个式子应相等.
(3x+20)
4x
(4x – 25)
这批书的总数是一个定值,表示它的两个式子相等.
3x+20 = 4x-25.
解:设这个班有x名学生,
根据题意得:
x = 45.
答:这个班有45名学生.
解得:
列一元一次方程解实际问题的一般步骤
1、审:审题,(借助表格,图表等提炼数学信息,理解问题中的基本数学关系)
2、设:设未知数(直接设法、间接设法)
3、找:找出能够表示题中全部含义的一个等量关系
4、列:根据等量关系列出方程
5、解:解所列出的方程,求出未知数的值
6、答:检验所求的解是否符合题意,在写出答案
议一议
? 解题后的反思
扩展
某件工作,甲单独做x小时完成,乙单独做y小时完成,
1)甲、乙的工作效率分别为??? ????、??? ?? ??;
2)甲、乙合作m天可以完成的工作量为??? ??? ?或??? ? ???。
例3 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
列表分析:
人均效率
人数
时间
工作量
前一部分工作
x
4
后一部分工作
x+2
8
×
=
×
×
×
=
工作量之和等于总工作量1
解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
练习:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设 x多少天可以铺好这条管线.
依题意得: ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
抓住配套关系,设出未知数,根据配套关系列出方程,通过解方程来解决问题
五、强化训练
1、一项工程甲单独做要35天完成,乙单独需40天完成,甲先单独4天,然后两人合作x天完成这项工程,则可列的方程是( )
A. B.
C. D.
D
五、强化训练
2、一批宿舍,若每间住2人,则有10人无法安排;若每间住3人,则有8间无住.这批宿舍的间数为( )
A.30 B. 34 C. 35 D. 40
3、甲、乙两人练习跑步,从同一地点出发,甲每分钟跑250米,乙每分钟跑200米,甲比乙晚出发3分钟,结果两人同时到达终点,则两人所跑的总路_____米.
B
3000
五、强化训练
4、一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设要x天可以铺好这条管线,据题意得
( + )x=1 解之得 x = 8
答:要8天可以铺好这条管线。
第一课时 配套问题与工程问题
第三章 一元一次方程
学习目标
学习目标
1.会通过列方程解决“配套问题”和“工程问题”;
2.掌握列方程解决实际问题的一般步骤;
3.通过列方程解决实际问题的过程,体会建模思想。
重点
建立模型解决实际问题的一般方法。
难点
列方程解决“配套问题”和“工程问题”。
课前回顾(解一元一次方程的步骤及注意事项)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}步骤
具体做法
依据
注意事项
去分母
在方程两边都乘以各分母的最小公倍数
等式
性质2
不要漏乘不含分母的项
去括号
一般先去小括号,再去中括号,最后去大括号
分配律 去括号法则
不要漏乘括号中的每一项
移项
把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号
移项法则
1)移动的项一定要变号,
不移的项不变号
2)注意项较多时不要漏项
合并同类项
把方程变为ax=b
(a≠0 ) 的最简形式
合并同类项法则
1)把系数相加
2)字母和字母的指数不变
系数化为1
等式性质2
解的分子,分母位置不要颠倒
生活中,有很多需要进行配套的问题,比如我们使用的餐桌需要和椅子进行配套,你能举出生活中一些配套的问题吗?
情境导入
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
二、应用与探究
?思考 与分析
(1)请你一边阅读题目,一边画出文段中的关键信息,并用自己的语言概括出来.
“每天生产的螺钉和螺母刚好配套”如何用数学语言表示?
“1个螺钉要配2个螺母”
“螺母的总产量=螺钉总产量的2 倍”
列表分析:
产品类型
生产人数
每人产量
总产量
螺钉
螺母
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
22﹣x
螺母总产量是螺钉的2倍
1 200
2 000
x
每人每天的工作效率×人数=每天的工作量(产品数量)
由“螺母的总产量=螺钉总产量的2 倍”可得方程
?
例题解析
解:设应安排 x 名工人生产螺钉,________名工人生产螺母,由题意得
2×1 200 x = 2 000 ( 22 - x).
去括号,得
2 400 x = 44 000 – 2 000 x.
移项,合并同类项,得
4 400 x = 44 000.
x = 10.
生产螺母的人数为
22 – x = 12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
(22 – x)
实际问题
设安排x名工人
生产 螺钉
解方程
一元一次方程的解(x=a)
双检验
实际问题
的答案
规划分工使两种产品数量上成为配套的问题
设未知数、 列方程
一元一次方程
带入方程成立
符合实际意义
2 000(22 - x)=2 ×1 200 x
x=10
22 - x =12
解一元一次方程
应该安排10名工人生产螺钉,12名工人生产螺母
(2)实际问题到数学问题再到实际问题的解的模型.
例2.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
分析:
设这个班有x名学生.每人分3本,共分出3x本,加上剩余的20本,这批书共 ____ 本;每人分4本,需要___本,减去缺的25本,这批书共______本.
这批书的总数是一个定值,表示它的两个式子应相等.
(3x+20)
4x
(4x – 25)
这批书的总数是一个定值,表示它的两个式子相等.
3x+20 = 4x-25.
解:设这个班有x名学生,
根据题意得:
x = 45.
答:这个班有45名学生.
解得:
列一元一次方程解实际问题的一般步骤
1、审:审题,(借助表格,图表等提炼数学信息,理解问题中的基本数学关系)
2、设:设未知数(直接设法、间接设法)
3、找:找出能够表示题中全部含义的一个等量关系
4、列:根据等量关系列出方程
5、解:解所列出的方程,求出未知数的值
6、答:检验所求的解是否符合题意,在写出答案
议一议
? 解题后的反思
扩展
某件工作,甲单独做x小时完成,乙单独做y小时完成,
1)甲、乙的工作效率分别为??? ????、??? ?? ??;
2)甲、乙合作m天可以完成的工作量为??? ??? ?或??? ? ???。
例3 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
列表分析:
人均效率
人数
时间
工作量
前一部分工作
x
4
后一部分工作
x+2
8
×
=
×
×
×
=
工作量之和等于总工作量1
解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
练习:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设 x多少天可以铺好这条管线.
依题意得: ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
抓住配套关系,设出未知数,根据配套关系列出方程,通过解方程来解决问题
五、强化训练
1、一项工程甲单独做要35天完成,乙单独需40天完成,甲先单独4天,然后两人合作x天完成这项工程,则可列的方程是( )
A. B.
C. D.
D
五、强化训练
2、一批宿舍,若每间住2人,则有10人无法安排;若每间住3人,则有8间无住.这批宿舍的间数为( )
A.30 B. 34 C. 35 D. 40
3、甲、乙两人练习跑步,从同一地点出发,甲每分钟跑250米,乙每分钟跑200米,甲比乙晚出发3分钟,结果两人同时到达终点,则两人所跑的总路_____米.
B
3000
五、强化训练
4、一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设要x天可以铺好这条管线,据题意得
( + )x=1 解之得 x = 8
答:要8天可以铺好这条管线。
