人教版数学八上册:14.1.1同底数幂的乘法-课件(16张PPT)
文档属性
| 名称 | 人教版数学八上册:14.1.1同底数幂的乘法-课件(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 269.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 07:09:38 | ||
图片预览






文档简介
14.1 整式的乘法
第十四章 整式的乘法与因式分解
14.1.1 同底数幂的乘法
导入新课
神威·太湖之光超级计算机是由国家并行计算机工程技术研究中心研制的超级计算机.北京时间2016年6月20日,在法兰克福世界超算大会(ISC)上,“神威·太湖之光”超级计算机系统登顶榜单之首,成为世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
1017 ×103
1017 ×103
1017 和103这两个因数底数相同,是同底数的幂的形式.
我们把形如1017 ×103这种运算叫作同底数幂的乘法.
根据乘方的意义,如何计算1017 ×103?
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
探究
(2)a3·a2=a( )
7
5
m+n
(m、n都是正整数).
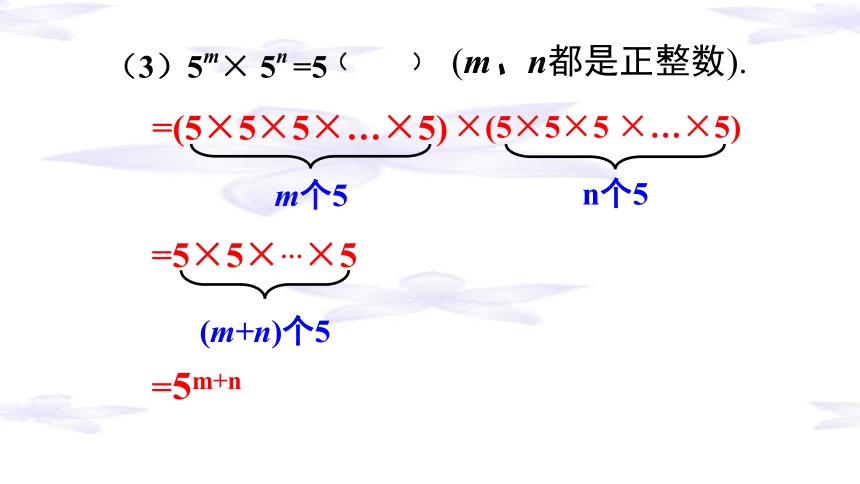
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
(m、n都是正整数).
(1)25×22=2 ( )
探究
(2)a3·a2=a( )
7
5
m+n
(m、n都是正整数).
猜想
am · an =a( )
m+n
(m、n都是正整数).
小组活动
am · an =a( )
(m、n都是正整数).
m+n
各组思考并写出推导过程,然后小组交流,
派代表展示并分析推导过程,时间3分钟
am · an = am+n (m、n都是正整数).
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法法则:
一般地,对于任意底数a与任意正整数m , n ,
(1) 105×106=_____________;
(2) 23 ·24=_____________;
(3) 2 3 ·24 ·25 =_____________;
抢答
计算:
1011
27
212
am· an· ap = am+n+p (m、n、p都是正整数)
am · an = am+n (m、n都是正整数).
同底数幂的乘法法则:
推广:
典例精析
例1 计算:
(1)x2 · x5 ;
(2)a · a6;
(3)(-2) × (-2)4 × (-2)3;
(4) xm · x3m+1.
a=a1
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
×
×
×
×
b6
2b3
=x8
a9
(-x)8
练一练
结果:①底数不变
②指数相加
方法归纳
条件:①乘法
②底数相同
(2)b3+b3=b6
(3)a·a5·a3=a8
?
(5)(-x)4·(-x)4=(-x)16
课堂练习:课本96页练习
(抄题,拍照上传)
?
同底数幂乘法法则的逆用
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
课堂小结
同底数幂的乘法法则
am·an=am+n (m,n都是正整数)
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
?
?
?
作业
第十四章 整式的乘法与因式分解
14.1.1 同底数幂的乘法
导入新课
神威·太湖之光超级计算机是由国家并行计算机工程技术研究中心研制的超级计算机.北京时间2016年6月20日,在法兰克福世界超算大会(ISC)上,“神威·太湖之光”超级计算机系统登顶榜单之首,成为世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
1017 ×103
1017 ×103
1017 和103这两个因数底数相同,是同底数的幂的形式.
我们把形如1017 ×103这种运算叫作同底数幂的乘法.
根据乘方的意义,如何计算1017 ×103?
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
探究
(2)a3·a2=a( )
7
5
m+n
(m、n都是正整数).
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
(m、n都是正整数).
(1)25×22=2 ( )
探究
(2)a3·a2=a( )
7
5
m+n
(m、n都是正整数).
猜想
am · an =a( )
m+n
(m、n都是正整数).
小组活动
am · an =a( )
(m、n都是正整数).
m+n
各组思考并写出推导过程,然后小组交流,
派代表展示并分析推导过程,时间3分钟
am · an = am+n (m、n都是正整数).
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法法则:
一般地,对于任意底数a与任意正整数m , n ,
(1) 105×106=_____________;
(2) 23 ·24=_____________;
(3) 2 3 ·24 ·25 =_____________;
抢答
计算:
1011
27
212
am· an· ap = am+n+p (m、n、p都是正整数)
am · an = am+n (m、n都是正整数).
同底数幂的乘法法则:
推广:
典例精析
例1 计算:
(1)x2 · x5 ;
(2)a · a6;
(3)(-2) × (-2)4 × (-2)3;
(4) xm · x3m+1.
a=a1
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
×
×
×
×
b6
2b3
=x8
a9
(-x)8
练一练
结果:①底数不变
②指数相加
方法归纳
条件:①乘法
②底数相同
(2)b3+b3=b6
(3)a·a5·a3=a8
?
(5)(-x)4·(-x)4=(-x)16
课堂练习:课本96页练习
(抄题,拍照上传)
?
同底数幂乘法法则的逆用
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
课堂小结
同底数幂的乘法法则
am·an=am+n (m,n都是正整数)
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
?
?
?
作业
