人教版数学九年级上册24.1.1圆课件(20张)
文档属性
| 名称 | 人教版数学九年级上册24.1.1圆课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 00:00:00 | ||
图片预览


文档简介
24.1圆的定义与性质
人教九年级上册第24章
问题1:1、观察下列生活中的图片,找一找你所熟悉的图形
·
r
O
A
圆的旋转定义
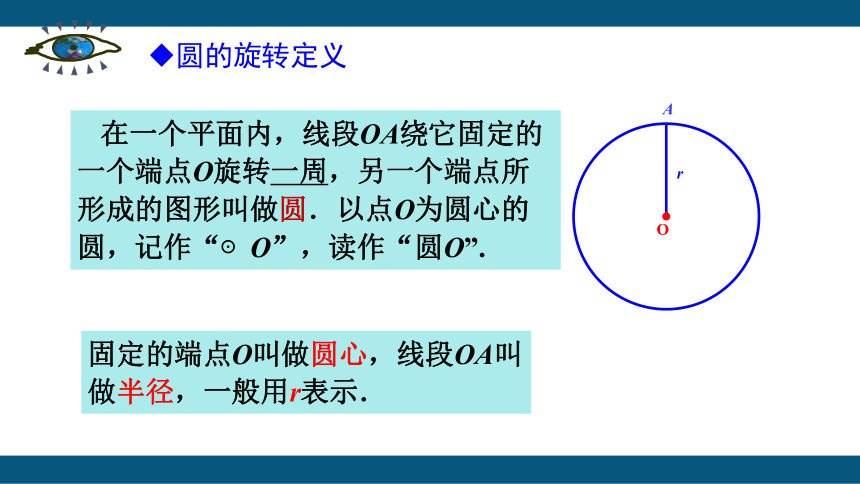
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
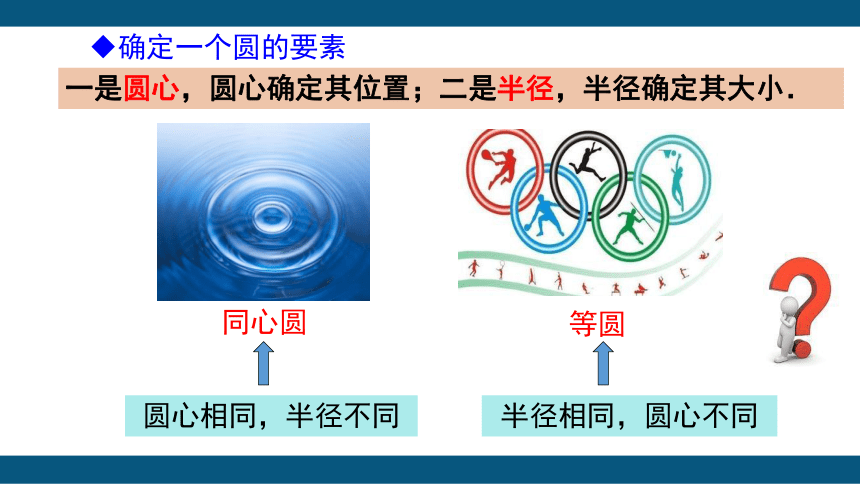
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
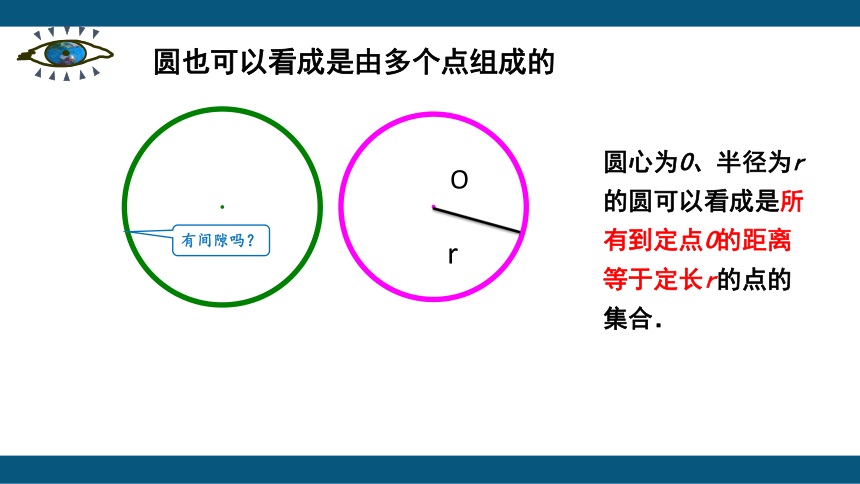
有间隙吗?
O
r
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
圆也可以看成是由多个点组成的
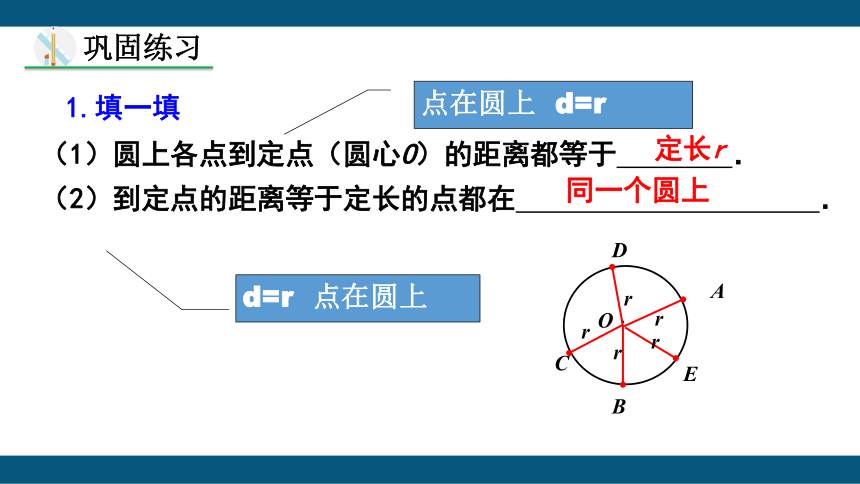
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
1.填一填
定长r
同一个圆上
D
O
·
A
C
E
r
r
r
r
r
B
点在圆上 d=r
d=r 点在圆上
巩固练习
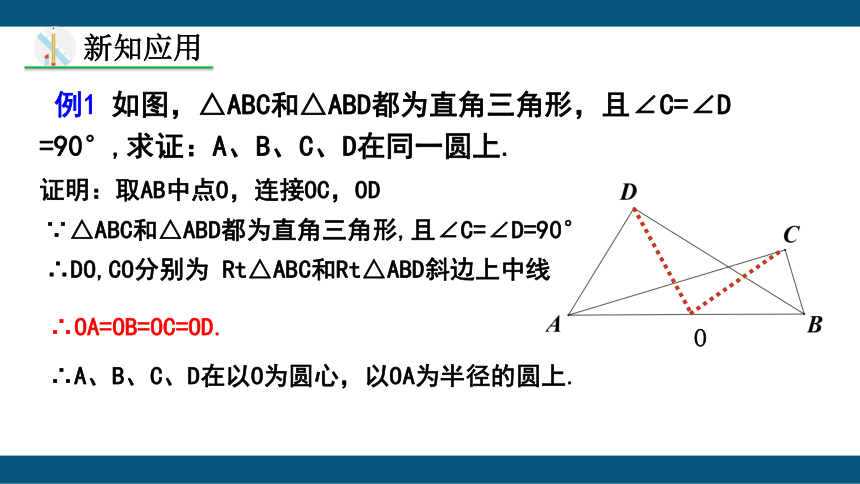
例1 如图,△ABC和△ABD都为直角三角形,且∠C=∠D
=90°,求证:A、B、C、D在同一圆上.
证明:取AB中点O,连接OC,OD
∵△ABC和△ABD都为直角三角形,且∠C=∠D=90°
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
O
∴DO,CO分别为 Rt△ABC和Rt△ABD斜边上中线
∴OA=OB=OC=OD.
新知应用
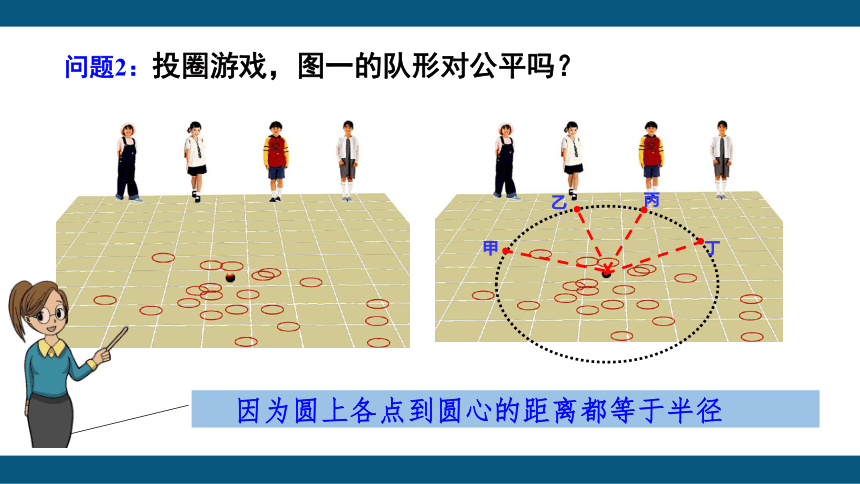
问题2:投圈游戏,图一的队形对公平吗?
甲
丙
乙
丁
因为圆上各点到圆心的距离都等于半径
o
?
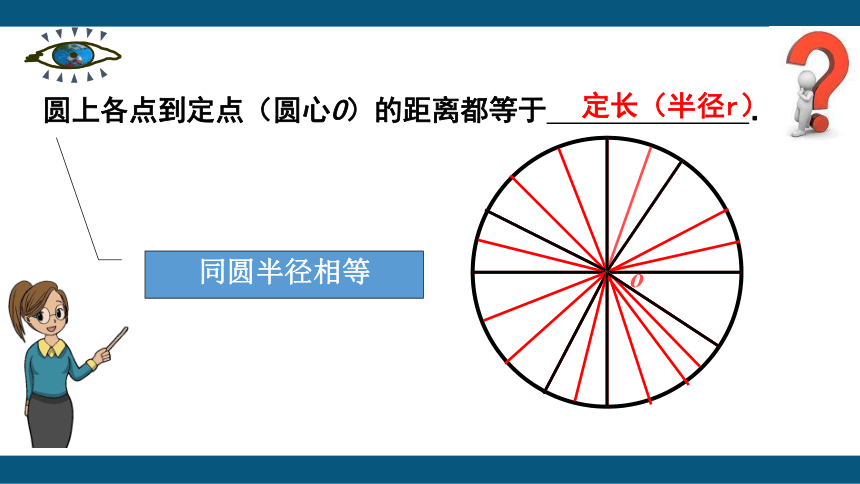
圆上各点到定点(圆心O)的距离都等于 .
定长(半径r)
同圆半径相等
例2 如图,点A、B、C在⊙0上,∠BAC=40°,∠C=20°,
则∠B的度数为.
点拨:连接OA,OA=OC?∠OAC=20°
OA=OB,∠B=∠OAB=60°
∠BAC=40°?∠OAB=60°
新知应用
已知,如图,在⊙0中,AB为弦,C、D两点在弦AB上,且AC=BD,
求证:OC=OD.
证明:∵OA=OB,
∴∠A=∠B
又∵AC=BD,
∴△AOC ?△BOD,
∴OC=OD
巩固练习
弦:
C
B
·
O
A
连接圆上任意两点的线段(如图中的AC)叫做弦。
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦.
注意
·
C
O
A
B
连接OC,
在△AOC中,根据三角形三边关系有AO+OC>AC,
而AB=2OA,AO=OC,所以AB>AC.
探索:直径是圆中最长的弦。为什么?
弧:
圆弧,简弧.
记作 AB ,
读作“圆弧AB”或“弧AB”.
(
·
C
O
A
B
·
C
O
A
B
半圆 如图中的半圆AB ;
劣弧 如图中的AC ;
优弧 如图中的ABC.
(
(
等圆:
·
C
O
A
能够重合的两个圆叫做等圆.
·
C
O1
A
容易看出:
等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
结论:等弧仅仅存在于同圆或者等圆中.
实际上这两条弧弯曲程度不同
请写出以点A为端点的优弧及劣弧;
请写出以点A为端点的弦及直径
请任选一条弦,写出这条弦所对的弧.
.
弦AF , AB , AC .其中弦AB又是直径.
答案不唯一,如:弦AF,它所对的弧是 .
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
AF
(
ACD.
(
ACF.
(
ACF
(
巩固练习
1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,劣弧有 条.
直径
半径
一
二
四
四
2.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .
7cm或3cm
A
B
C
D
O
F
E
巩固练习
归纳总结
01 圆的定义
02 同圆半径相等
03 圆的相关概念
·
C
O
A
B
同学们再见!
人教九年级上册第24章
人教九年级上册第24章
问题1:1、观察下列生活中的图片,找一找你所熟悉的图形
·
r
O
A
圆的旋转定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
有间隙吗?
O
r
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
圆也可以看成是由多个点组成的
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
1.填一填
定长r
同一个圆上
D
O
·
A
C
E
r
r
r
r
r
B
点在圆上 d=r
d=r 点在圆上
巩固练习
例1 如图,△ABC和△ABD都为直角三角形,且∠C=∠D
=90°,求证:A、B、C、D在同一圆上.
证明:取AB中点O,连接OC,OD
∵△ABC和△ABD都为直角三角形,且∠C=∠D=90°
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
O
∴DO,CO分别为 Rt△ABC和Rt△ABD斜边上中线
∴OA=OB=OC=OD.
新知应用
问题2:投圈游戏,图一的队形对公平吗?
甲
丙
乙
丁
因为圆上各点到圆心的距离都等于半径
o
?
圆上各点到定点(圆心O)的距离都等于 .
定长(半径r)
同圆半径相等
例2 如图,点A、B、C在⊙0上,∠BAC=40°,∠C=20°,
则∠B的度数为.
点拨:连接OA,OA=OC?∠OAC=20°
OA=OB,∠B=∠OAB=60°
∠BAC=40°?∠OAB=60°
新知应用
已知,如图,在⊙0中,AB为弦,C、D两点在弦AB上,且AC=BD,
求证:OC=OD.
证明:∵OA=OB,
∴∠A=∠B
又∵AC=BD,
∴△AOC ?△BOD,
∴OC=OD
巩固练习
弦:
C
B
·
O
A
连接圆上任意两点的线段(如图中的AC)叫做弦。
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦.
注意
·
C
O
A
B
连接OC,
在△AOC中,根据三角形三边关系有AO+OC>AC,
而AB=2OA,AO=OC,所以AB>AC.
探索:直径是圆中最长的弦。为什么?
弧:
圆弧,简弧.
记作 AB ,
读作“圆弧AB”或“弧AB”.
(
·
C
O
A
B
·
C
O
A
B
半圆 如图中的半圆AB ;
劣弧 如图中的AC ;
优弧 如图中的ABC.
(
(
等圆:
·
C
O
A
能够重合的两个圆叫做等圆.
·
C
O1
A
容易看出:
等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
结论:等弧仅仅存在于同圆或者等圆中.
实际上这两条弧弯曲程度不同
请写出以点A为端点的优弧及劣弧;
请写出以点A为端点的弦及直径
请任选一条弦,写出这条弦所对的弧.
.
弦AF , AB , AC .其中弦AB又是直径.
答案不唯一,如:弦AF,它所对的弧是 .
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
AF
(
ACD.
(
ACF.
(
ACF
(
巩固练习
1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,劣弧有 条.
直径
半径
一
二
四
四
2.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .
7cm或3cm
A
B
C
D
O
F
E
巩固练习
归纳总结
01 圆的定义
02 同圆半径相等
03 圆的相关概念
·
C
O
A
B
同学们再见!
人教九年级上册第24章
同课章节目录
