人教版数学七年级上册:3.1.2 等式的性质 第2课时用等式的性质解方程 课件(21张PPT)
文档属性
| 名称 | 人教版数学七年级上册:3.1.2 等式的性质 第2课时用等式的性质解方程 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 21:01:26 | ||
图片预览








文档简介
3.1.2 等式的性质
第二课时
用等式的性质解方程
复习回顾:
1. 什么叫方程?
2.什么叫方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
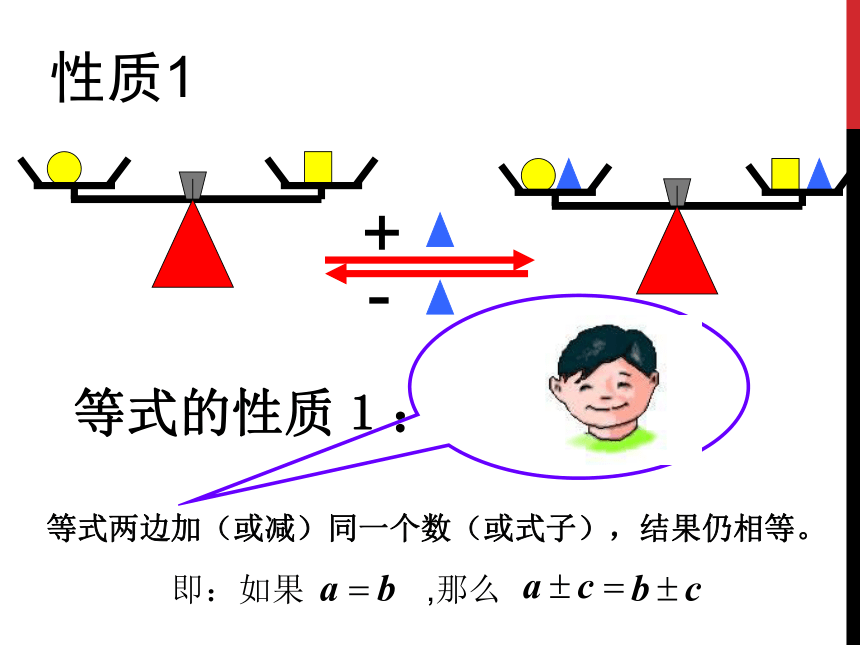
+
-
等式两边加(或减)同一个数(或式子),结果仍相等。
等式的性质1:
即:如果 ,那么
性质1
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式的性质2:
即:如果 ,那么
如果 (c≠0) ,那么
×3
÷3
性质2
用等式的性质变形时需注意:
①两边必须同时进行计算;
②加(或减),乘(或除以)的数必须是同一个数;
③除数不能为0.
(1)如果x=y,那么??????????????????? (????? )?????????
(2)如果x=y,那么??????????????????? (????? )
(3)如果x=y,那么??????????????????? (????? )
(4)如果x=y,那么??????????????????? (????? )
(5)如果x=y,那么??????????????????? (????? )?
1.判断对错,对的说明根据等式的哪一条性质;错的说出为什么?
×
√
×
×
√
针对练习
(2) 怎样从等式 3+x=1 得到等式 x =-2?
(3) 怎样从等式 4x=12 得到等式 x =3?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
2.(1) 怎样从等式 x-5= y-5 得到等式 x = y ?
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b?
(2) 怎样从等式 3+x=1 得到等式 x =-2?
(3) 怎样从等式 4x=12 得到等式 x =3?
(6) 从 a+2=b+2 能不能得到 a=b,为什么?
(7) 从-3a=-3b 能不能得到 a=b,为什么?
(5) 从 x = y 能不能得到 ,为什么?
能,根据等式的性质2,两边同时除以9
能,根据等式的性质1,两边同时减2
能,根据等式的性质2,两边同时除以-3
解一元一次 方程就是利用等式的性质
把方程转化为x=a(常数)的形式,那么我
们应该如何运用等式的性质来解方程?
问题思考:
学习目标
知识与能力
1.通过解一元一次方程进一步理解等式的性质.2.会用等式的性质解简单的(两次运用等式的性质)一元一次方程.
过程与方法
通过用等式的性质解方程的过程,初步体验解方程中的”化归”意识.
情感态度与价值观
培养言必有据的思维能力和良好的思维品质.
学习重点
用等式的性质解方程.
学习难点
需要两次运用等式的性质,并且有一定的思维顺序.
一: 利用等式的性质解方程
例2 利用等式的性质解下列方程:
(1) x + 7 = 26
解:
得
方程两边同时减去7,
x + 7 = 26
-7
-7
化简,得 =
x
19
小结:解一元一次方程要“化归”为“ x=a ”的形式.
探究:
探究:
两边同时除以-5,
得
解:
方程
(2) -5x = 20
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
化简,得
x=-4
-5x÷(-5)= 20 ÷(-5)
解:方程两边同时加上5,得
化简,得
方程两边同时
乘 -3,
化简,得 x =
-27
x=-27是原方程的解吗?
思考:对比(1),(3)有什么新特点 ?
(3)
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,
将 x = -27 代入方程 的左边,
方程的左右两边相等,所以 x = -27 是原方程的解.
注意:要代入原方程
针对训练:
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
解:(1)两边同时减去6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加上1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加上-1,得
两边同时乘以-3,得x=9.
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边是一个未知数项、且未知数项的系数是1,右边是一个常数项。
课堂小结
A
1. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
当堂检测
2.下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
D
3.利用等式性质解下列方程:
(1)x - 5 = 6 (2) 0.3x = 45
(3)2 - x = 3 (4)5x+4=0
(5) x+3= 6; (6) 0.2x =4;
(7) -2x+4=0; (8)
1
4
4.已知关于x的方程 和方程3x -10 =5 的解相同,求m的值.
解:方程3x-10 =5的解为x =5,将其代入方程
,得到 ,解得m =2.
课后作业
1、作业本上: 习题3.1
2 、同步训练.
第二课时
用等式的性质解方程
复习回顾:
1. 什么叫方程?
2.什么叫方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
+
-
等式两边加(或减)同一个数(或式子),结果仍相等。
等式的性质1:
即:如果 ,那么
性质1
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式的性质2:
即:如果 ,那么
如果 (c≠0) ,那么
×3
÷3
性质2
用等式的性质变形时需注意:
①两边必须同时进行计算;
②加(或减),乘(或除以)的数必须是同一个数;
③除数不能为0.
(1)如果x=y,那么??????????????????? (????? )?????????
(2)如果x=y,那么??????????????????? (????? )
(3)如果x=y,那么??????????????????? (????? )
(4)如果x=y,那么??????????????????? (????? )
(5)如果x=y,那么??????????????????? (????? )?
1.判断对错,对的说明根据等式的哪一条性质;错的说出为什么?
×
√
×
×
√
针对练习
(2) 怎样从等式 3+x=1 得到等式 x =-2?
(3) 怎样从等式 4x=12 得到等式 x =3?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
2.(1) 怎样从等式 x-5= y-5 得到等式 x = y ?
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b?
(2) 怎样从等式 3+x=1 得到等式 x =-2?
(3) 怎样从等式 4x=12 得到等式 x =3?
(6) 从 a+2=b+2 能不能得到 a=b,为什么?
(7) 从-3a=-3b 能不能得到 a=b,为什么?
(5) 从 x = y 能不能得到 ,为什么?
能,根据等式的性质2,两边同时除以9
能,根据等式的性质1,两边同时减2
能,根据等式的性质2,两边同时除以-3
解一元一次 方程就是利用等式的性质
把方程转化为x=a(常数)的形式,那么我
们应该如何运用等式的性质来解方程?
问题思考:
学习目标
知识与能力
1.通过解一元一次方程进一步理解等式的性质.2.会用等式的性质解简单的(两次运用等式的性质)一元一次方程.
过程与方法
通过用等式的性质解方程的过程,初步体验解方程中的”化归”意识.
情感态度与价值观
培养言必有据的思维能力和良好的思维品质.
学习重点
用等式的性质解方程.
学习难点
需要两次运用等式的性质,并且有一定的思维顺序.
一: 利用等式的性质解方程
例2 利用等式的性质解下列方程:
(1) x + 7 = 26
解:
得
方程两边同时减去7,
x + 7 = 26
-7
-7
化简,得 =
x
19
小结:解一元一次方程要“化归”为“ x=a ”的形式.
探究:
探究:
两边同时除以-5,
得
解:
方程
(2) -5x = 20
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
化简,得
x=-4
-5x÷(-5)= 20 ÷(-5)
解:方程两边同时加上5,得
化简,得
方程两边同时
乘 -3,
化简,得 x =
-27
x=-27是原方程的解吗?
思考:对比(1),(3)有什么新特点 ?
(3)
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,
将 x = -27 代入方程 的左边,
方程的左右两边相等,所以 x = -27 是原方程的解.
注意:要代入原方程
针对训练:
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
解:(1)两边同时减去6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加上1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加上-1,得
两边同时乘以-3,得x=9.
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边是一个未知数项、且未知数项的系数是1,右边是一个常数项。
课堂小结
A
1. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
当堂检测
2.下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
D
3.利用等式性质解下列方程:
(1)x - 5 = 6 (2) 0.3x = 45
(3)2 - x = 3 (4)5x+4=0
(5) x+3= 6; (6) 0.2x =4;
(7) -2x+4=0; (8)
1
4
4.已知关于x的方程 和方程3x -10 =5 的解相同,求m的值.
解:方程3x-10 =5的解为x =5,将其代入方程
,得到 ,解得m =2.
课后作业
1、作业本上: 习题3.1
2 、同步训练.
