北京市第43中学2020-2021学年高二上学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 北京市第43中学2020-2021学年高二上学期期中考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 460.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 10:58:59 | ||
图片预览




文档简介
北京市第四十三中学2020—2021学年度第一学期期中
高二数学
2020.11.
试卷满分:150分
考试时间:120分钟
一.选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,则=
(
)
A.
B.
C.
D.
2.若,,则是(
)
A.第四象限角
B.第三象限角
C.第二象限角
D.第一象限角
3.下列函数中,既是偶函数又存在零点的是(
)
A.
B.
C.
D.
4.已知角的顶点在坐标原点,始边与轴正半轴重合,终边经过点,则(
)
A.
B.
C.
D.
5.
,两点之间的距离为(
)
A.
B.
C.
D.
6.已知向量,且,那么(
)
A.
B.
C.
D.
7.圆的圆心到直线的距离为(
)
A.2
B.
C.1
D.
8.已知是两条不同直线,是三个不同平面,下列命题中正确的是(
)
A.若则
B.若则
C.若则
D.若则
9.
圆上的点到直线的最大距离与最小距离的差是(
)
A.36
B.
C.
18
D.
10.
如图,在边长为2的正方体ABCD—A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为
(
)
A.
B.
2
C.
D.
3
二.填空题(本大题共6小题,每题5分,共30分,把答案填在答题纸上)
11.
已知,,则
12.
过点(1,0)且与直线平行的直线方程是
13.
直线的倾斜角为
,x轴上截距为
14.
在中,,则______,的面积为_______.
15.
已知直线与圆交于两点,若,则____.
16.
已知点P是直线上的一点,过P作圆的切线,
切点为A,则切线长的最小值为__
___.
三.解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤)
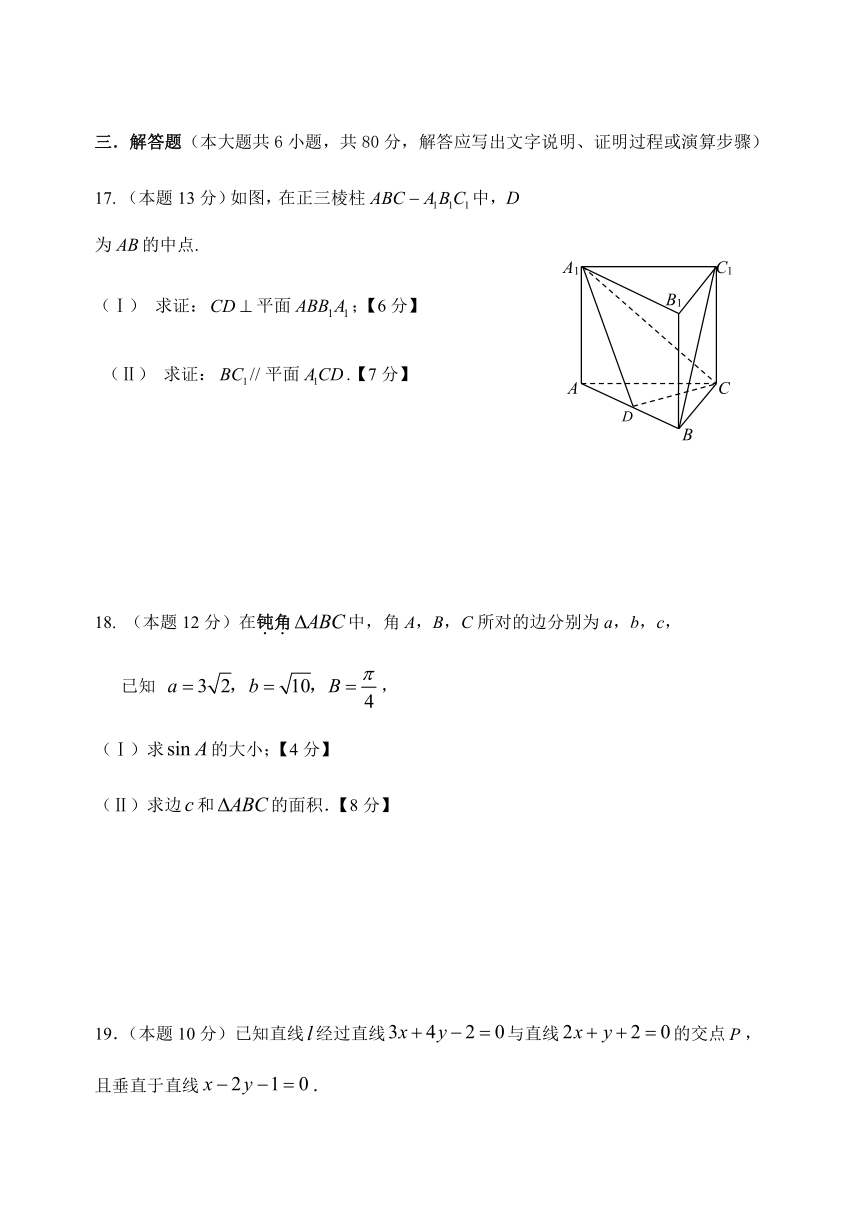
17.
(本题13分)如图,在正三棱柱中,为的中点.
(Ⅰ)
求证:平面;【6分】
(Ⅱ)
求证:平面.【7分】
18.
(本题12分)在钝角中,角A,B,C所对的边分别为a,b,c,
已知
,
(Ⅰ)求的大小;【4分】
(Ⅱ)求边和的面积.【8分】
19.(本题10分)已知直线经过直线与直线的交点,且垂直于直线.
(Ⅰ)求直线的方程.【6分】
(Ⅱ)求直线与两坐标轴围成的三角形的面积.【4分】
20.
(本题15分)如图,在四棱锥中,底面为正方形,
底面,,为棱的中点.
(Ⅰ)求证;【4分】
(Ⅱ)求直线与平面所成角的正弦值;【7分】
(Ⅲ)求点A到平面PBD的距离。【4分】
21.(本题15分)
已知圆C:,直线过定点.
(Ⅰ)若直线与圆C相切,求直线的方程;【5分】
(Ⅱ)若直线与圆C相交于P,Q两点,求的面积的最大值,并求此时直线的方程.【10分】
22.
(本题15分)如图,在三棱柱中,侧棱垂直于底面,,,,分别为,的中点.
(Ⅰ)求证:;
(Ⅱ)求证:∥平面;【5分】
(Ⅱ)求证:∥平面;【5分】
(Ⅲ)在棱上是否存在一点,
使得平面平面?说明理由.
【5分】
参考答案
一。选择题
1.
C
2.
B
3.D
4.B
5.C
6.A
7.B
8.D
9.B
10.D
二。填空题
11.
12.
13.
;
14.
;
15.
16.
三。解答题
17.(Ⅰ)证明:因为正三棱柱,为的中点,
所以,底面.
…………………1分
又因为底面,
所以.
…………………3分
又因为,平面,平面,
所以平面.
…………………6分
(Ⅱ)证明:如图,连接,设,连接,
…………………7分
由正三棱柱,得,
又因为在中,,
所以,
…………………10分
又因为平面,平面,
所以平面.
…………………13分
18【答案】(1)(2),
【详解】:(1)因为
,
所以。。。。。4分
(2)因为所以
得即所以
因为三角形是钝角三角形,所以舍去
所以………12分
错解:(2)没有注意到三角形是钝角三角形,检验cosA<0得到两组解
所以
19.答案:(1)(2)1
【详解】
(),解得,则点的坐标为.
由于点的坐标是,且所求直线与直线垂直,
可设所求直线的方程为.
将点坐标代入得,解得.
故所求直线的方程为.
.。。。。。。。。。。。。6分
()由直线的方程知它在轴,轴上的截距分别是,,
所以直线与两坐标轴围成的三角形的面积.
。。。。。。。。。。。10分
20【答案】
(Ⅰ)证明:因为底面, 所以.
因为,
所以.
由于,
所以有.…………………4分
(Ⅱ)解:依题意,以点为原点建立空间直角坐标系(如图),
不妨设,可得,,,.
由为棱的中点,得.
向量,.
设为平面的法向量,则即.
不妨令,可得(1,1,1)为平面的一个法向量.
所以
.
所以,直线与平面所成角的正弦值为.
…………………11分
(Ⅲ)解:
…………………15分
21.【答案】(1)或
【分析】
(1)通过直线的斜率存在与不存在两种情况,利用直线的方程与圆C相切,圆心到直线的距离等于半径即可求解直线的方程;
(2)设直线方程为,求出圆心到直线的距离、求得弦长,得到的面积的表达式,利用二次函数求出面积的最大值时的距离,然后求出直线的斜率,即可得到直线的方程.
【详解】
(1)①若直线l1的斜率不存在,则直线l1:x=1,符合题意.
。。。。。2分
②若直线l1斜率存在,设直线l1的方程为,即.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,即:
,解之得
.
所求直线l1的方程是或.
。。。。。。。。。。。5分
(2)直线与圆相交,斜率必定存在,且不为0,
设直线方程为,
则圆心到直线l1的距离
又∵△CPQ的面积
=
∴当d=时,S取得最大值2.
∴=
∴
k=1
或k=7
所求直线l1方程为
x-y-1=0或7x-y-7=0
.
.。。。。。。。15分
【点睛】
本题主要考查了直线与圆的位置关系的应用,其中解答中涉及到直线与圆相切,圆的弦长公式,以及三角形的面积公式和二次函数的性质等知识点的综合考查,其中熟记直线与圆的位置关系的应用,合理准确计算是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.
22.
解:(Ⅰ)在三棱柱中,
因为侧棱垂直于底面,
所以平面.
所以.
因为,,
所以平面.
因为平面,
所以.
………5分
(Ⅱ)取中点,连结,.
则∥,且,
又因为∥,且,
所以∥,且.
所以四边形为平行四边形.
所以∥.
又平面,平面,
所以∥平面.
………10分
(Ⅲ)在棱上存在点,且为的中点.
连接.
在正方形中,
因为为中点,
所以△≌△.
所以.
所以.
由(Ⅰ)可得平面,
因为//,
所以平面.
因为平面,
所以.
因为,
所以平面.
因为平面,
所以平面平面.
………15分
高二数学
2020.11.
试卷满分:150分
考试时间:120分钟
一.选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,则=
(
)
A.
B.
C.
D.
2.若,,则是(
)
A.第四象限角
B.第三象限角
C.第二象限角
D.第一象限角
3.下列函数中,既是偶函数又存在零点的是(
)
A.
B.
C.
D.
4.已知角的顶点在坐标原点,始边与轴正半轴重合,终边经过点,则(
)
A.
B.
C.
D.
5.
,两点之间的距离为(
)
A.
B.
C.
D.
6.已知向量,且,那么(
)
A.
B.
C.
D.
7.圆的圆心到直线的距离为(
)
A.2
B.
C.1
D.
8.已知是两条不同直线,是三个不同平面,下列命题中正确的是(
)
A.若则
B.若则
C.若则
D.若则
9.
圆上的点到直线的最大距离与最小距离的差是(
)
A.36
B.
C.
18
D.
10.
如图,在边长为2的正方体ABCD—A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为
(
)
A.
B.
2
C.
D.
3
二.填空题(本大题共6小题,每题5分,共30分,把答案填在答题纸上)
11.
已知,,则
12.
过点(1,0)且与直线平行的直线方程是
13.
直线的倾斜角为
,x轴上截距为
14.
在中,,则______,的面积为_______.
15.
已知直线与圆交于两点,若,则____.
16.
已知点P是直线上的一点,过P作圆的切线,
切点为A,则切线长的最小值为__
___.
三.解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤)
17.
(本题13分)如图,在正三棱柱中,为的中点.
(Ⅰ)
求证:平面;【6分】
(Ⅱ)
求证:平面.【7分】
18.
(本题12分)在钝角中,角A,B,C所对的边分别为a,b,c,
已知
,
(Ⅰ)求的大小;【4分】
(Ⅱ)求边和的面积.【8分】
19.(本题10分)已知直线经过直线与直线的交点,且垂直于直线.
(Ⅰ)求直线的方程.【6分】
(Ⅱ)求直线与两坐标轴围成的三角形的面积.【4分】
20.
(本题15分)如图,在四棱锥中,底面为正方形,
底面,,为棱的中点.
(Ⅰ)求证;【4分】
(Ⅱ)求直线与平面所成角的正弦值;【7分】
(Ⅲ)求点A到平面PBD的距离。【4分】
21.(本题15分)
已知圆C:,直线过定点.
(Ⅰ)若直线与圆C相切,求直线的方程;【5分】
(Ⅱ)若直线与圆C相交于P,Q两点,求的面积的最大值,并求此时直线的方程.【10分】
22.
(本题15分)如图,在三棱柱中,侧棱垂直于底面,,,,分别为,的中点.
(Ⅰ)求证:;
(Ⅱ)求证:∥平面;【5分】
(Ⅱ)求证:∥平面;【5分】
(Ⅲ)在棱上是否存在一点,
使得平面平面?说明理由.
【5分】
参考答案
一。选择题
1.
C
2.
B
3.D
4.B
5.C
6.A
7.B
8.D
9.B
10.D
二。填空题
11.
12.
13.
;
14.
;
15.
16.
三。解答题
17.(Ⅰ)证明:因为正三棱柱,为的中点,
所以,底面.
…………………1分
又因为底面,
所以.
…………………3分
又因为,平面,平面,
所以平面.
…………………6分
(Ⅱ)证明:如图,连接,设,连接,
…………………7分
由正三棱柱,得,
又因为在中,,
所以,
…………………10分
又因为平面,平面,
所以平面.
…………………13分
18【答案】(1)(2),
【详解】:(1)因为
,
所以。。。。。4分
(2)因为所以
得即所以
因为三角形是钝角三角形,所以舍去
所以………12分
错解:(2)没有注意到三角形是钝角三角形,检验cosA<0得到两组解
所以
19.答案:(1)(2)1
【详解】
(),解得,则点的坐标为.
由于点的坐标是,且所求直线与直线垂直,
可设所求直线的方程为.
将点坐标代入得,解得.
故所求直线的方程为.
.。。。。。。。。。。。。6分
()由直线的方程知它在轴,轴上的截距分别是,,
所以直线与两坐标轴围成的三角形的面积.
。。。。。。。。。。。10分
20【答案】
(Ⅰ)证明:因为底面, 所以.
因为,
所以.
由于,
所以有.…………………4分
(Ⅱ)解:依题意,以点为原点建立空间直角坐标系(如图),
不妨设,可得,,,.
由为棱的中点,得.
向量,.
设为平面的法向量,则即.
不妨令,可得(1,1,1)为平面的一个法向量.
所以
.
所以,直线与平面所成角的正弦值为.
…………………11分
(Ⅲ)解:
…………………15分
21.【答案】(1)或
【分析】
(1)通过直线的斜率存在与不存在两种情况,利用直线的方程与圆C相切,圆心到直线的距离等于半径即可求解直线的方程;
(2)设直线方程为,求出圆心到直线的距离、求得弦长,得到的面积的表达式,利用二次函数求出面积的最大值时的距离,然后求出直线的斜率,即可得到直线的方程.
【详解】
(1)①若直线l1的斜率不存在,则直线l1:x=1,符合题意.
。。。。。2分
②若直线l1斜率存在,设直线l1的方程为,即.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,即:
,解之得
.
所求直线l1的方程是或.
。。。。。。。。。。。5分
(2)直线与圆相交,斜率必定存在,且不为0,
设直线方程为,
则圆心到直线l1的距离
又∵△CPQ的面积
=
∴当d=时,S取得最大值2.
∴=
∴
k=1
或k=7
所求直线l1方程为
x-y-1=0或7x-y-7=0
.
.。。。。。。。15分
【点睛】
本题主要考查了直线与圆的位置关系的应用,其中解答中涉及到直线与圆相切,圆的弦长公式,以及三角形的面积公式和二次函数的性质等知识点的综合考查,其中熟记直线与圆的位置关系的应用,合理准确计算是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.
22.
解:(Ⅰ)在三棱柱中,
因为侧棱垂直于底面,
所以平面.
所以.
因为,,
所以平面.
因为平面,
所以.
………5分
(Ⅱ)取中点,连结,.
则∥,且,
又因为∥,且,
所以∥,且.
所以四边形为平行四边形.
所以∥.
又平面,平面,
所以∥平面.
………10分
(Ⅲ)在棱上存在点,且为的中点.
连接.
在正方形中,
因为为中点,
所以△≌△.
所以.
所以.
由(Ⅰ)可得平面,
因为//,
所以平面.
因为平面,
所以.
因为,
所以平面.
因为平面,
所以平面平面.
………15分
同课章节目录
