角平分线的性质(二)
图片预览


文档简介
(共15张PPT)
角平分线的性质(二)
1:怎样画一个已知角的角平分线;
2:角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:
到角的两边的距离相等的点在角平分线上。
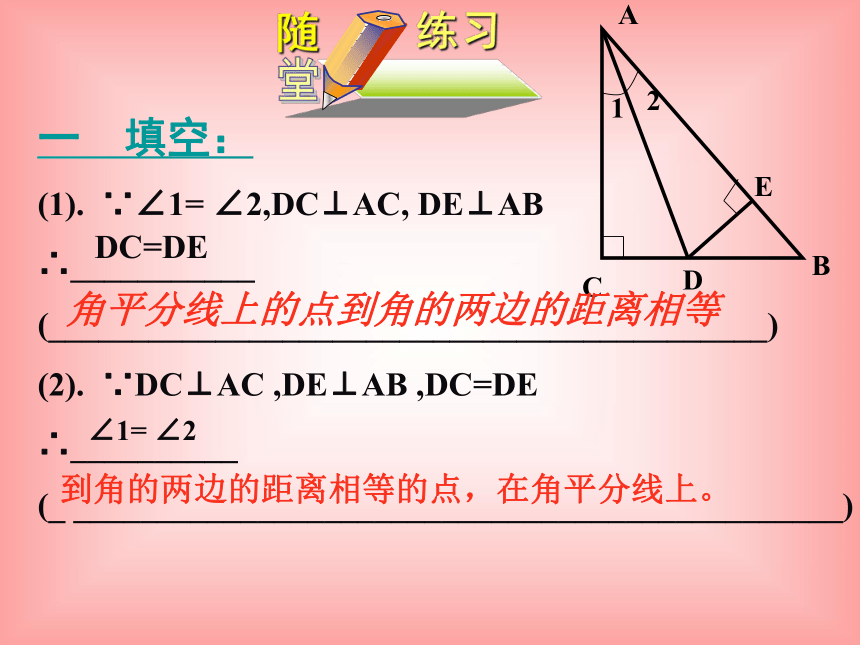
一 填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(2). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到角的两边的距离相等的点,在角平分线上。
角平分线上的点到角的两边的距离相等
随
练习
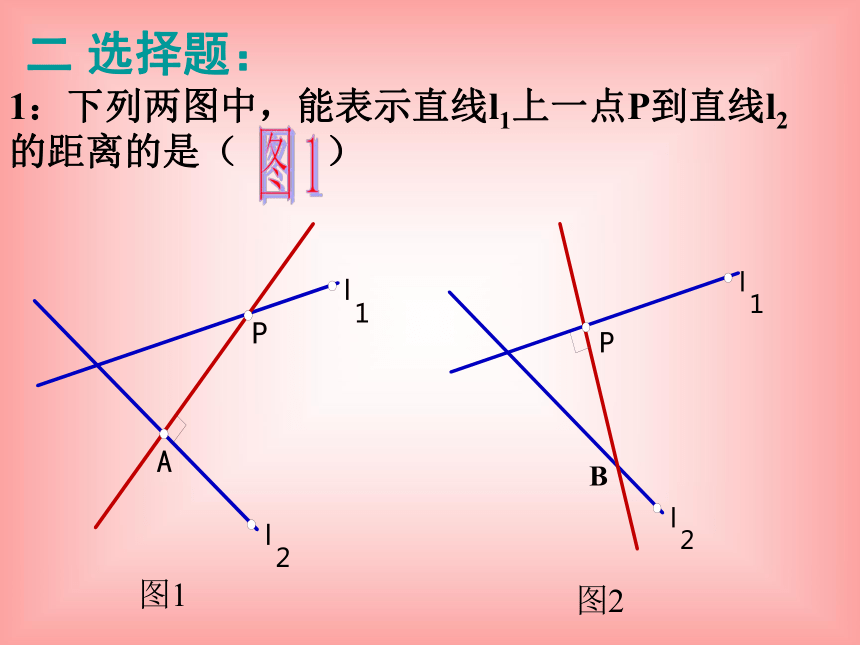
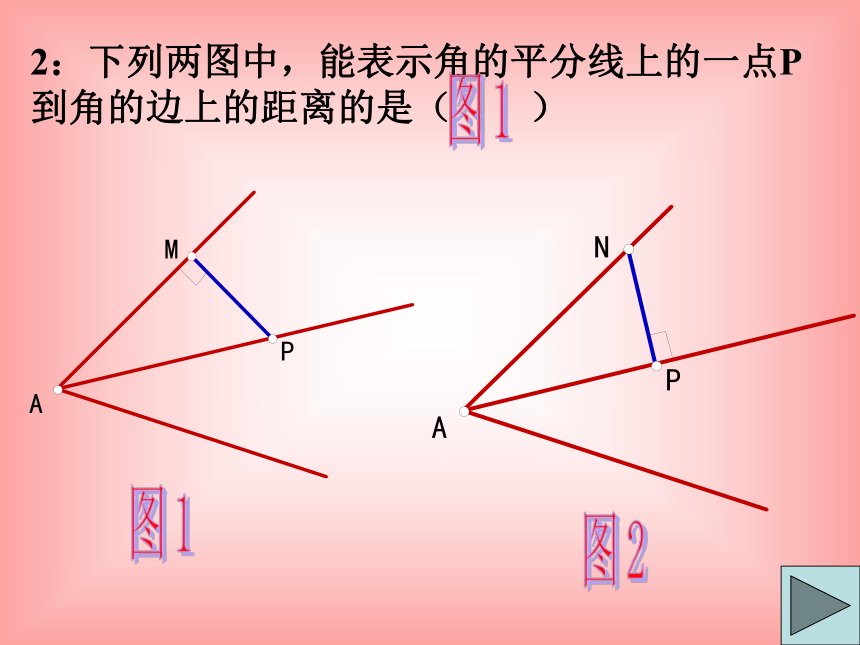
图1
图2
B
1:下列两图中,能表示直线l1上一点P到直线l2的距离的是( )
二 选择题:
2:下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
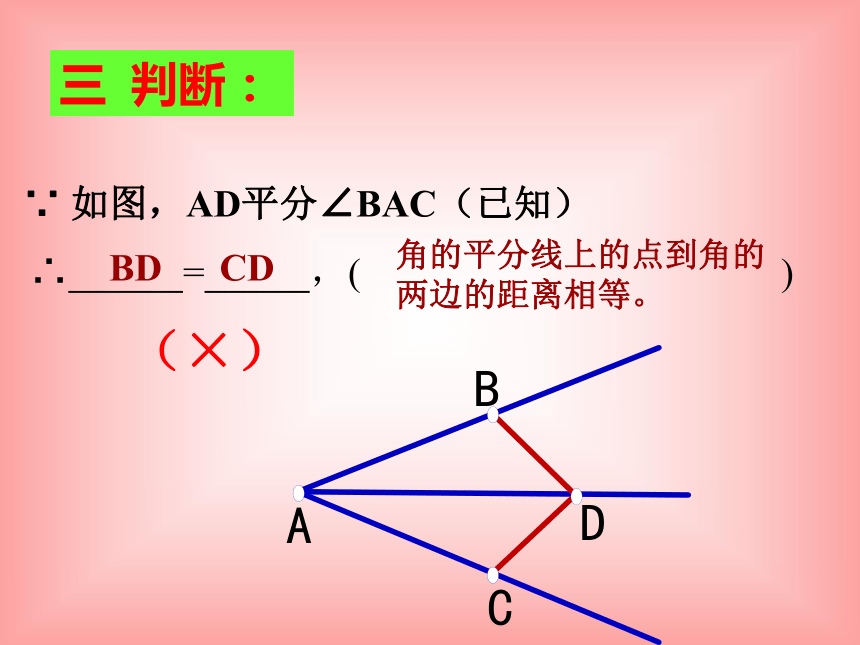
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角的平分线上的点到角的两边的距离相等。
BD CD
三 判断:
(×)
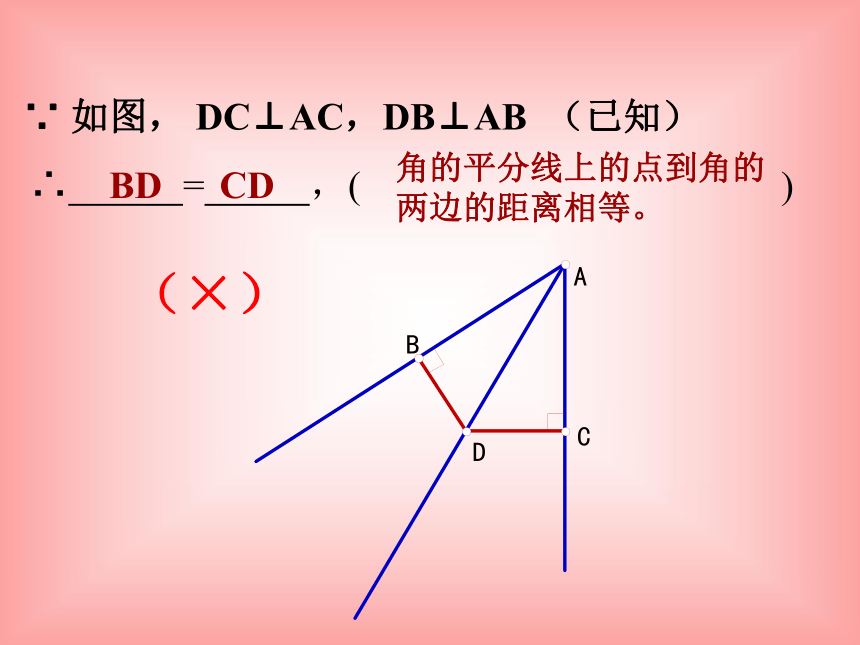
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角的平分线上的点到角的两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DE⊥AB (已知)
∴ = ,( )
DB
DC
角的平分线上的点到角的两边的距离相等。
√
四 问答 :1、如图,在Rt△ABC 中,
做完本题后,你对角平分线,又增加了什么认识
思考
角平分线的性质,
为我们证明两线段相等 又提供了新的方法与途径。
A
B
C
BD是∠B 的平分线 ,
DE⊥AB,垂足为E,
E
DE与DC 相等吗?
D
答:
DE=BC。
∵ BD是∠ABC的平分线 (D在∠ABC的平分线上)
又∵ DE⊥BA,垂足为E,
∴ DE=BC。
为什么?
DC⊥BC,垂足为E,
1:如图所示,四边形ABCD中, AB=AD, AB⊥BC,AD⊥DC,
求证:BC=DC。
2:如图所示, △ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E。
求证:MD=ME。
3:如图所示,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点。
求证: ∠BDP= ∠CDP
再 见
尺规作角的平分线
观察领悟作法,探索思考证明方法:
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于.
2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
角平分线的性质(二)
1:怎样画一个已知角的角平分线;
2:角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:
到角的两边的距离相等的点在角平分线上。
一 填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(2). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到角的两边的距离相等的点,在角平分线上。
角平分线上的点到角的两边的距离相等
随
练习
图1
图2
B
1:下列两图中,能表示直线l1上一点P到直线l2的距离的是( )
二 选择题:
2:下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角的平分线上的点到角的两边的距离相等。
BD CD
三 判断:
(×)
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角的平分线上的点到角的两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DE⊥AB (已知)
∴ = ,( )
DB
DC
角的平分线上的点到角的两边的距离相等。
√
四 问答 :1、如图,在Rt△ABC 中,
做完本题后,你对角平分线,又增加了什么认识
思考
角平分线的性质,
为我们证明两线段相等 又提供了新的方法与途径。
A
B
C
BD是∠B 的平分线 ,
DE⊥AB,垂足为E,
E
DE与DC 相等吗?
D
答:
DE=BC。
∵ BD是∠ABC的平分线 (D在∠ABC的平分线上)
又∵ DE⊥BA,垂足为E,
∴ DE=BC。
为什么?
DC⊥BC,垂足为E,
1:如图所示,四边形ABCD中, AB=AD, AB⊥BC,AD⊥DC,
求证:BC=DC。
2:如图所示, △ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E。
求证:MD=ME。
3:如图所示,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点。
求证: ∠BDP= ∠CDP
再 见
尺规作角的平分线
观察领悟作法,探索思考证明方法:
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于.
2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
