9.有理数的乘方
图片预览






文档简介
(共25张PPT)
教学目标:
1、理解有理数乘方的意义
2、能进行有理数的乘方运算
3、通过实例感受到底数大于1时,乘 方运算的结果增长得很快
知识回顾:
有理数的乘法法则:
两数相乘,同号得正,异号得负,绝对值相乘。
几个不等于零的数相乘,积的符号由负因数的个数确定,当负因数的个数为奇数时,积为负;当负因数的个数为偶数时,积为正。
任何数与0相乘,积仍为0.
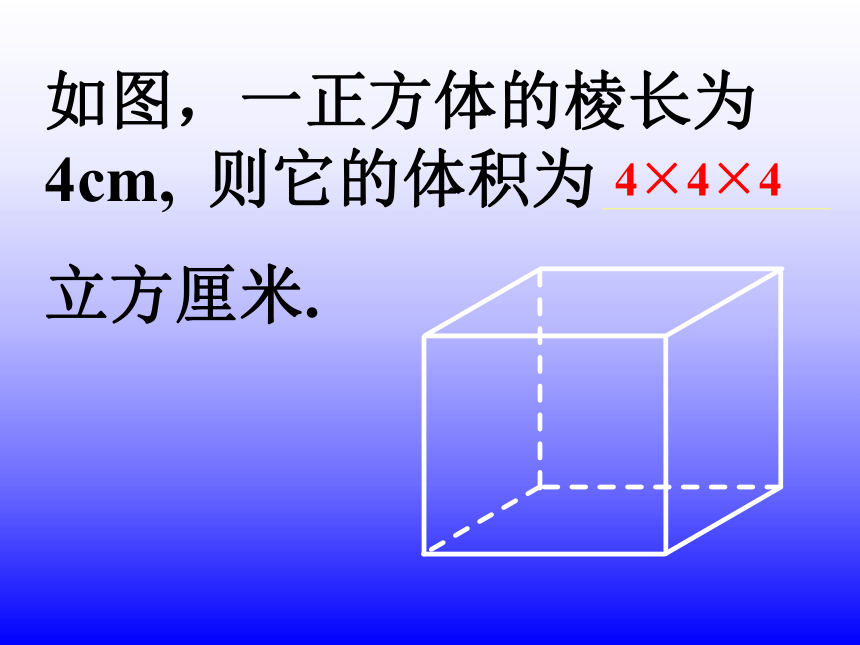
如图,一正方体的棱长为4cm, 则它的体积为
立方厘米.
4×4×4
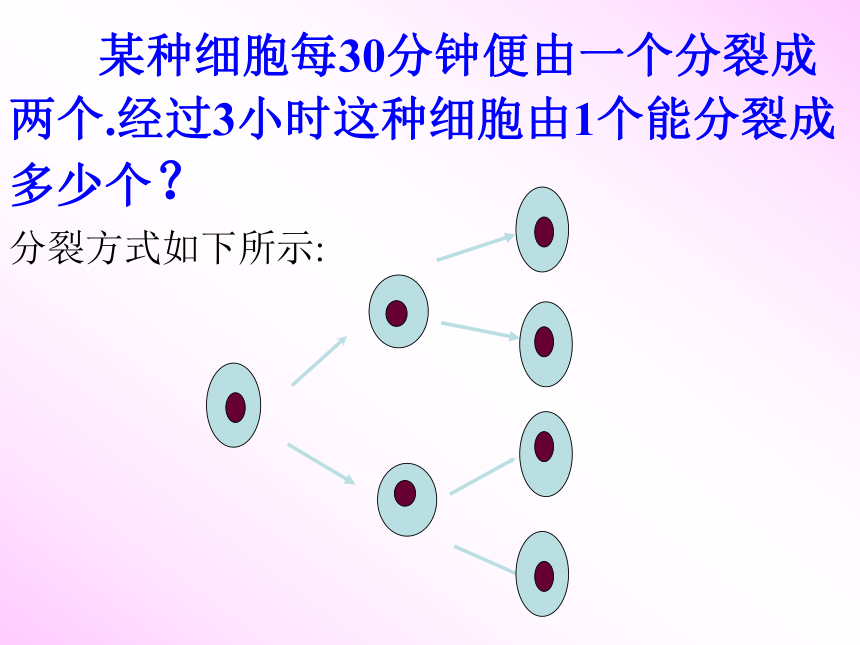
某种细胞每30分钟便由一个分裂成两个.经过3小时这种细胞由1个能分裂成多少个?
分裂方式如下所示:
这个细胞分裂一次可得多少个细胞
那么,3小时共分裂了多少次
答:一次得:
两次 :
三次 :
2个;
2×2个;
2×2×2个;
六次 : 2×2×2×2×2×2个.
分裂两次呢
分裂三次呢
分析:
请比较正方体的体积值式子:
4×4×4和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
它们有什么相同点
答:它们都是乘法;并且它们各自的因数都相同.
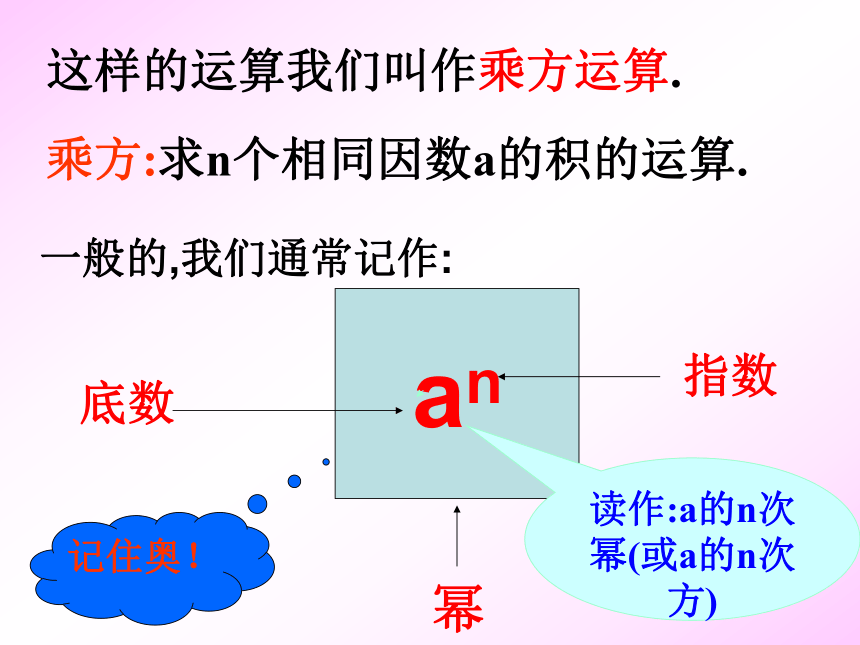
这样的运算我们叫作乘方运算.
乘方:求n个相同因数a的积的运算.
一般的,我们通常记作:
an
底数
指数
幂
读作:a的n次幂(或a的n次方)
记住奥!
练习一:
1、在74中,底数是----------,指数是--------。
3、判断下列各式是否成立:
(1)23=2x3;
(2)32=23;
(3)(-3)2=-32.
7
4
5
(×)
(×)
(×)
指出下列各数读作什么?其中底数是什么?指数是什么?表示什么意义 (用乘法表示)
23 32
(-4)2 -42
底数为负数和分数要加括号!
8
1
练习二:
例1 计算:
(1)5 3 (2)(-3)4
(3)
解:(1)53 =
5×5×5
=125;
(2)(-3)4
=(-3) ×(-3) ×(-3) ×(-3)
=81;
典例解析:
(1)23 (2)32
算一算:
(3)(-4)2 (4) -42
(5)
(6)
例2 计算:
(1)102 103 104
典例解析:
解:(1)
102
=100;
103
=1000;
104 =10000;
(2)
(-10)2
=100
(-10)3
=-1000;
(-10)4 =10000;
105=100000;
(-10)5=-100000;
观察例2,你能发现指数与结果之间有什么关系?与同伴进行交流。
答:10的几次方,1后面就有几
个0;
想一想:
观察下列几组数据,看看你能发现什么规律?与同伴进行交流。
(1)
102
=100;
103
=1000;
104 =10000;
24=16;
105=100000;
(2)
23=8;
25=32;
26=64;
正数的任何次幂都是正数!
(3)
(-10)2=100;
(-10)4=10000;
(-10)6=1000000;
(4)
(-10)3=-1000;
(-10)5=-100000;
(-10)7=-10000000;
负数的偶数次幂都是正数
负数的奇数次幂都是负数
有理数的乘方法则:
答:正数的任何次幂都是正数
负数的奇次幂是负数
负数的偶次幂是正数
1、(-1)3=( )
2、(-1)10=( )
3、(-1)99=( )
4、(-1)100=( )
-1
-1
1
1
通过这节课你学会了哪些知识?
课堂达标
1、在(-6)3中,底数是------,指数是------。
2、在-43中,底数是-----,指数是--------。
3、计算:
4、一个数的平方是16,这个数可能是几?一个数的平方可能是0吗?
5、1米长的木棒,第一次截去一半,第二次截去剩下的一半,如此接下去,截7次后剩下的木棒有多长?
试一试:
拓展延伸
=-9
=-(-8)=8
教学目标:
1、理解有理数乘方的意义
2、能进行有理数的乘方运算
3、通过实例感受到底数大于1时,乘 方运算的结果增长得很快
知识回顾:
有理数的乘法法则:
两数相乘,同号得正,异号得负,绝对值相乘。
几个不等于零的数相乘,积的符号由负因数的个数确定,当负因数的个数为奇数时,积为负;当负因数的个数为偶数时,积为正。
任何数与0相乘,积仍为0.
如图,一正方体的棱长为4cm, 则它的体积为
立方厘米.
4×4×4
某种细胞每30分钟便由一个分裂成两个.经过3小时这种细胞由1个能分裂成多少个?
分裂方式如下所示:
这个细胞分裂一次可得多少个细胞
那么,3小时共分裂了多少次
答:一次得:
两次 :
三次 :
2个;
2×2个;
2×2×2个;
六次 : 2×2×2×2×2×2个.
分裂两次呢
分裂三次呢
分析:
请比较正方体的体积值式子:
4×4×4和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
它们有什么相同点
答:它们都是乘法;并且它们各自的因数都相同.
这样的运算我们叫作乘方运算.
乘方:求n个相同因数a的积的运算.
一般的,我们通常记作:
an
底数
指数
幂
读作:a的n次幂(或a的n次方)
记住奥!
练习一:
1、在74中,底数是----------,指数是--------。
3、判断下列各式是否成立:
(1)23=2x3;
(2)32=23;
(3)(-3)2=-32.
7
4
5
(×)
(×)
(×)
指出下列各数读作什么?其中底数是什么?指数是什么?表示什么意义 (用乘法表示)
23 32
(-4)2 -42
底数为负数和分数要加括号!
8
1
练习二:
例1 计算:
(1)5 3 (2)(-3)4
(3)
解:(1)53 =
5×5×5
=125;
(2)(-3)4
=(-3) ×(-3) ×(-3) ×(-3)
=81;
典例解析:
(1)23 (2)32
算一算:
(3)(-4)2 (4) -42
(5)
(6)
例2 计算:
(1)102 103 104
典例解析:
解:(1)
102
=100;
103
=1000;
104 =10000;
(2)
(-10)2
=100
(-10)3
=-1000;
(-10)4 =10000;
105=100000;
(-10)5=-100000;
观察例2,你能发现指数与结果之间有什么关系?与同伴进行交流。
答:10的几次方,1后面就有几
个0;
想一想:
观察下列几组数据,看看你能发现什么规律?与同伴进行交流。
(1)
102
=100;
103
=1000;
104 =10000;
24=16;
105=100000;
(2)
23=8;
25=32;
26=64;
正数的任何次幂都是正数!
(3)
(-10)2=100;
(-10)4=10000;
(-10)6=1000000;
(4)
(-10)3=-1000;
(-10)5=-100000;
(-10)7=-10000000;
负数的偶数次幂都是正数
负数的奇数次幂都是负数
有理数的乘方法则:
答:正数的任何次幂都是正数
负数的奇次幂是负数
负数的偶次幂是正数
1、(-1)3=( )
2、(-1)10=( )
3、(-1)99=( )
4、(-1)100=( )
-1
-1
1
1
通过这节课你学会了哪些知识?
课堂达标
1、在(-6)3中,底数是------,指数是------。
2、在-43中,底数是-----,指数是--------。
3、计算:
4、一个数的平方是16,这个数可能是几?一个数的平方可能是0吗?
5、1米长的木棒,第一次截去一半,第二次截去剩下的一半,如此接下去,截7次后剩下的木棒有多长?
试一试:
拓展延伸
=-9
=-(-8)=8
