鲁科版 必修1 第1节 匀变速直线运动的规律课件40张PPT
文档属性
| 名称 | 鲁科版 必修1 第1节 匀变速直线运动的规律课件40张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-17 19:28:25 | ||
图片预览






文档简介
平直公路上行驶的小车速度随时间变化的情况
8
10
12
14
16
12
9
6
3
0
4
3
2
1
0
t/s
5
?
?
一、匀变速直线运动的定义:
物体沿着一条直线,且加速度不变 的运动 ,叫做匀变速直线运动。
特点:速度均匀变化
1.公式:v t= v0+ a t
从运动开始到时刻t,
那么:时间的变化量就是△t=t-0
速度的变化量就是△v=vt-v0
所以a=△v/△t =(vt-v0)/△t
于是解得:vt=v0 +at
二、匀变速直线运动速度与时间的关系式
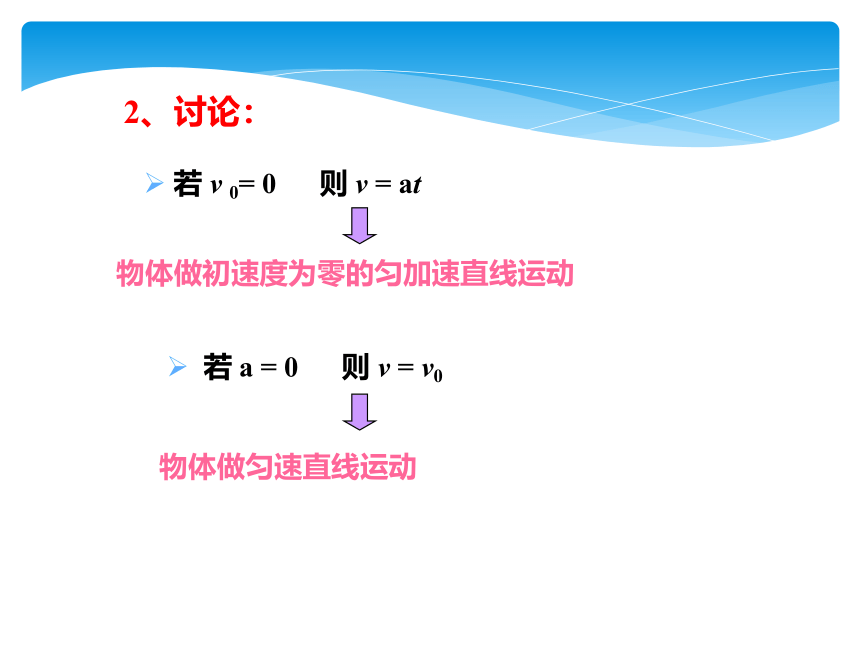
2、讨论:
若 v 0= 0 则 v = at
物体做初速度为零的匀加速直线运动
若 a = 0 则 v = v0
物体做匀速直线运动
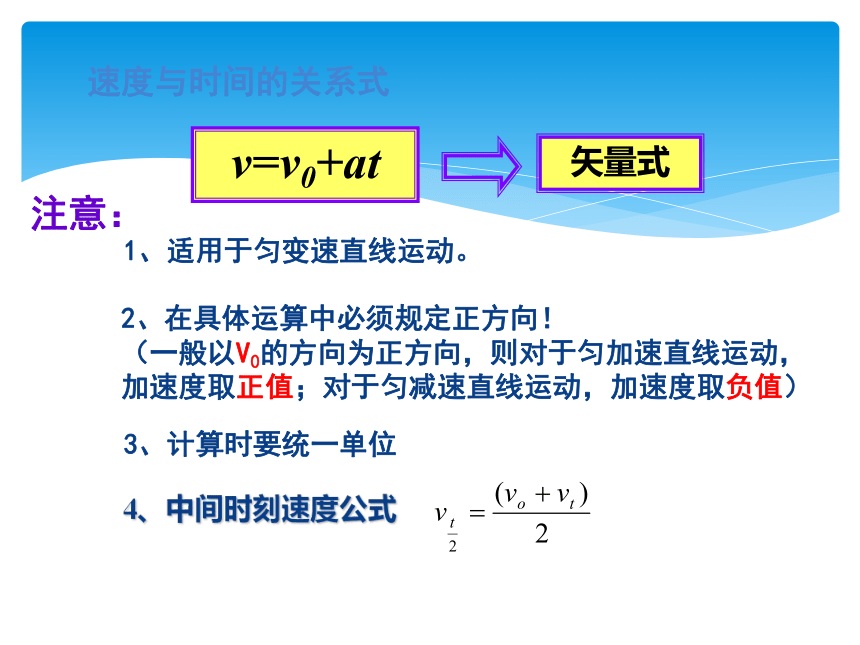
速度与时间的关系式
v=v0+at
矢量式
2、在具体运算中必须规定正方向!
(一般以V0的方向为正方向,则对于匀加速直线运动,加速度取正值;对于匀减速直线运动,加速度取负值)
1、适用于匀变速直线运动。
注意:
3、计算时要统一单位
4、中间时刻速度公式
×
×
×
×
甲车
t/s
v/ m·s-1
0
.
.
. .
.
.
.
.
.
.
.
1
4
3
2
5
3
12
6
9
v1
v2
t2
t1
.
.
t/s
0
1
2
3
4
V甲/m·s-1
0
3
6
9
12
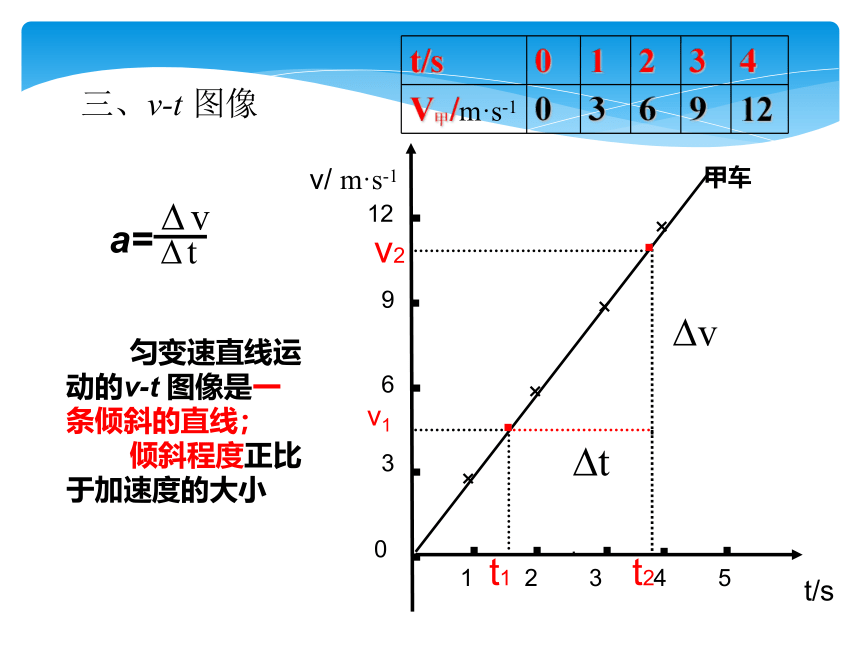
a=
三、v-t 图像
匀变速直线运动的v-t 图像是一条倾斜的直线;
倾斜程度正比于加速度的大小
4
2
8
0
υ/(m·s-1)
t/s
2
4
6
8
A
4
2
8
0
υ/(m·s-1)
t/s
2
4
6
8
B
①A、B两物体开始时刻的速度分别是多少?
② A、B两物体分别做什么运动,速度是如何变化的?
③ A、B两物体加速度分别是多少,谁的速度变化快?
匀加速直线运动
匀减速直线运动
思考:
3、匀变速直线运动的 v-t图象特点:
(1)一条倾斜的直线,
(2)该直线与纵轴的交点表示t=0时刻的初速度
(3)斜率表示加速度
(2) 可以知道任一瞬时速度所对应的时刻
4、从匀变速直线运动的v-t图象可获得的物理信息:
(1) 可以知道任一时刻所对应的瞬时速度
(3)可以求运动过程的的加速度
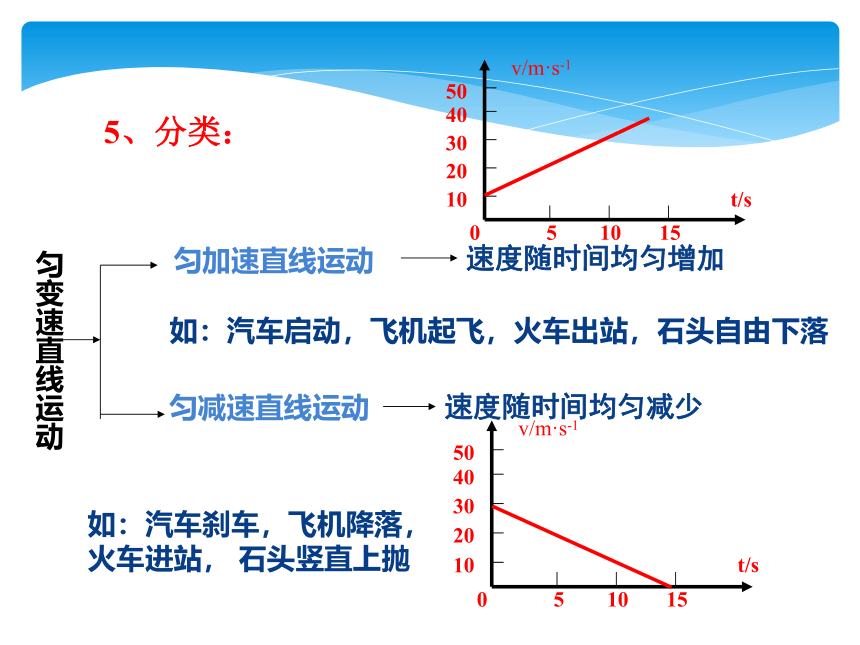
匀变速直线运动
匀加速直线运动
速度随时间均匀增加
匀减速直线运动
速度随时间均匀减少
如:汽车启动,飞机起飞,火车出站,石头自由下落
如:汽车刹车,飞机降落,火车进站, 石头竖直上抛
5、分类:
v/m·s-1
t/s
0
5
10
15
10
20
30
40
50
v/m·s-1
t/s
0
5
10
15
10
20
30
40
50
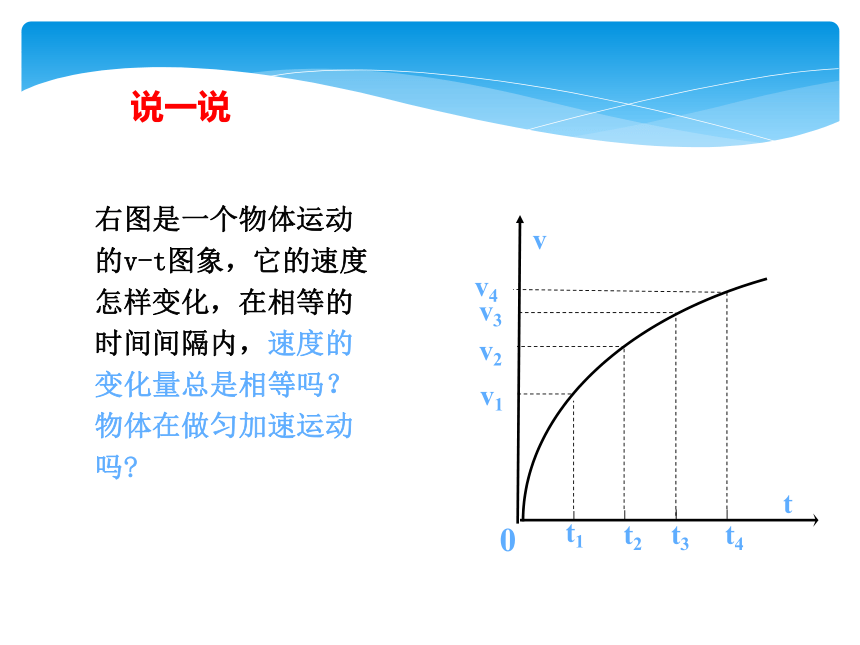
右图是一个物体运动
的v-t图象,它的速度
怎样变化,在相等的
时间间隔内,速度的
变化量总是相等吗?
物体在做匀加速运动
吗?
0
t1
t2
t3
t4
v1
v2
v3
v4
v
t
说一说
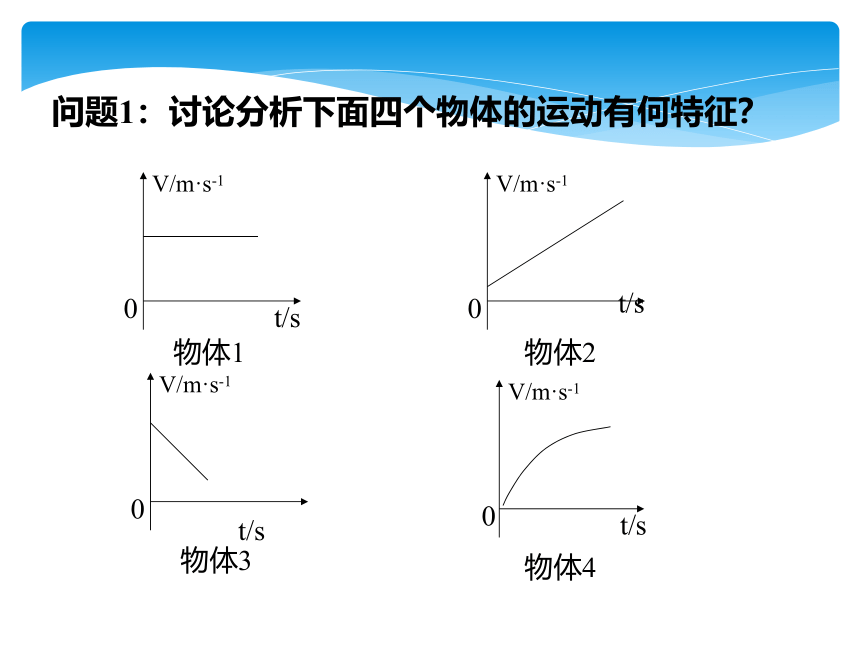
问题1:讨论分析下面四个物体的运动有何特征?
t/s
V/m·s-1
0
物体3
t/s
V/m·s-1
0
物体2
V/m·s-1
t/s
0
物体1
V/m·s-1
t/s
0
物体4
问题2、某质点运动的v-t图象如图所示 请描述出该质点的运动情况
t/s
1
2
3
4
v/m.s-1
4
-4
0
总结:描述一个物体的运动情况可以从以下几个方面进行:
(1)初速度情况;
(2)运动性质;
(3)运动时间
例题1:
1、关于匀变速直线运动,下列说法正确的是
A、做匀变速运动的物体相等时间内速度变化相等
B、加速运动一定是匀变速运动
C、减速运动一定不是匀变速运动
D、加速度和速度方向相同时,一定是做加速运动
AD
关于匀变速直线运动的理解
例题1、某汽车正以12m/s的速度在路面上匀速行驶,前方出现紧急情况需刹车,加速度大小是3m/s2,求汽车5s末的速度。
解:以初速方向为正方向
则v=v0+at=12+(-3) ×5m/s=-3m/s
正确解法:以初速方向为正方向
当车速减为零时,v=v0+at0=12-3t0=0
解得t0=4s
即4s末汽车已刹车完毕,所以5末时汽车处于静止状态,即速度为零。
刹车问题
注意:
(与实际相符)
注意:
1、该式是矢量式(应用时要先规定正方向);
2、刹车问题要先判断停止时间。
小结:
匀变速直线运动:质点沿着一条直线,且加速度不变的运动。
分类:匀加速直线运动
匀减速直线运动
图象法:图象是一条倾斜的直线
关系式:v = v0+ at
注意运用时确定公式中矢量的正负号
Vt与t的关系
研究方法:
小结:
课外继续学习——
课本P37 “作业”4、6、7;
第二课时
矩形面积有什么物理意义?
一、匀速直线运动的位移
1、x = v t
V=5m/s
t=3s
由此可见:
对于匀速直线运动,物体的位移的大小对应着v – t 图象中一块矩形的面积。
公式法
图象法
2、x = “面积”
v0
v
t
0
问题-探究:
在匀变速直线运动中,位移与它的v-t图象是否也有类似关系?
这里的“面积”
有什么物理意义?
某同学在“探究小车的速度随时间变化的规律”的实验中,算出小车经过各计数点的瞬时速度如下表所示。
计数点序号
0
1
2
3
4
5
时间t/s
0
0.1
0.2
0.3
0.4
0.5
速度V/(m/s)
0.38
0.63
0.88
1.13
1.38
1.63
如何估测从计数点0到计数点5的位移?
思考与讨论
思考:怎样把这样的科学思想方法应用到v-t图象上?
利用v-t图象探究——匀变速直线运动的位移
t
v
v0
O
t
v
v0
O
梯形的面积就代表做匀变速直线运动物体在0(此时速度为v0)到 t(此时速度为v)这段时间的位移。
t
v
v0
O
t
t
v
v0
O
t
5
2t
5
3t
5
4t
5
t
无限分割,选取微小,化变为不变! 求和,求极限!
思维体操
一小车在水平地面上作初速度为3m/s,加速度为5m/s2的匀加速直线运动,则经过3s的时间内小车行驶的位移为多少?
若一小车在水平地面上以速度为20m/s的速度,突然急刹车以为5m/s2的加速度作减速直线运动,则经过3s的时间内小车行驶的位移为多少?
通过这个练习你的收获是……
二、匀变速直线运动的位移
由图可知:梯形OABC的面积
S = (OC+AB)×OA / 2
代入各物理量得:
又 v t= v0 + at
得
t
v
v0
O
t
vt
A
B
C
2
1
t
vt
v
S
)
(
0
+
=
2
0
2
1
at
t
v
S
+
=
平均速度:
由v-t图像得:
(1)若物体作匀加速运动,则a与 v0
(2)若物体作匀减速运动,则a与 v0
------同向
------反向
at
V/(m·s-1)
t0
t/s
o
v
v0
at 2
V0t
at
o
V/(m·s-1)
t0
v
v0
t/s
S=V0t + at2
S=V0t + (-a)t2
二、匀变速直线运动的位移与时间关系
2
0
2
1
at
t
v
S
+
=
匀变速直线运动的S-t图象是一条抛物线
注意:S-t图象不是物体运动的轨迹
做一做
位移与时间的关系也可以用图象表示,这种图象叫做位移-时间图象, 即S-t图象.运用初中数学中学到的一次函数和二次函数知识,你能画出匀变速直线运动 的S-t图象的草图吗 ?
如果一位同学问:我们研究的是直线运动,为什么画出来的s-t图象不是直线?你应该怎样向他解释?
2
at
2
1
t
0
=v
s
+
S/m
t/s
2
1
3
4
5
6
7
8
思考:物体作直线运动,为何x-t图象是曲线?
匀变速直线运动位移公式的理论推导:
由
又匀变速直线运动的平均速度:
得:
又 vt = v0 + at
得:
例:一辆汽车以1m/s2的加速度行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
先用字母代表物理量进行运算,得出用已知量表达未知量的关系式,然后再把数值代入。
这样做能够清楚地看出未知量与已知量的关系,计算也比较简便。
例2、在平直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
解决刹车问题该注意什么呢?(可别往陷阱里跳啊!)
例:汽车以12m/s速度行驶,刹车做匀减速直线运动时的加速度大小为1m/s2。
求汽车从刹车直到停止时的位移。
v = v0 + a t
速度公式:
位移公式:
v 2 – v02 = 2 a s
注意:
1、优点:不需计算时间t 。
2、公式中四个矢量 vt、v0、a、s 要规定统一的正方向。
3、若v0 = 0 ,则vt = ?
s= v0 t + a t
1
2
—
2
【例题3】龟兔赛跑是大家小时侯就听过的故事,请叙述故事梗概并画出龟兔的 s—t 图和 v—t 图。
过程分析
1.开始时,乌龟以较小的速度作匀速直线运动,兔子飞快地跑一段。
2.途中,乌龟仍以较小的速度作匀速直线运动,兔子睡起了大觉。
3.结束时,乌龟还是以较小的速度作匀速直线运动,兔子又飞快地追赶。最终还是落后于乌龟。
匀速直线运动
匀变速直线运动
位移图象
速度图象
速度图象
图象
特征
直线
直线
直线
意义
直读位移
直读速度
直读速度
纵轴截距
初始位置
速度
初速度
斜率
速度
×
加速度
面积
×
位移
位移
直线运动图象信息的比较
小结
1、速度公式:
2、位移公式:
3、速度—位移公式:
x = v0 t + a t
1
2
—
2
v = v0 + a t
v 2 – v02 = 2 a x
(不涉及 x )
(不涉及 v )
(不涉及 t )
x = (v0 +vt) t
1
2
—
(不涉及 a )
例:已知汽车刹车后10s停下来,且汽车在匀减速直线运动时的加速度大小为1m/s2。
求汽车停止前最后1s内的位移。
末速度为零的匀减速直线运动可看成初速度为零,加速度大小相等的匀加速直线运动。
v0
A
B
0
a
a
附:解题技巧1
附:解题技巧2
某物体从静止开始做匀加速直线运动,经过4s达到2m/s,然后以这个速度运动12s最后做匀减速直线运动,经过4s停下来。求物体运动的距离
由v-t图像得
s = 1/2( 12+20 )×2 = 32 m
2
v/m/s
0
t/s
4 8 12 16 20
课外继续学习——
1、完成课本P37 “作业”2、3、5;
2、练习册第三章第一节练习。
谢 谢
8
10
12
14
16
12
9
6
3
0
4
3
2
1
0
t/s
5
?
?
一、匀变速直线运动的定义:
物体沿着一条直线,且加速度不变 的运动 ,叫做匀变速直线运动。
特点:速度均匀变化
1.公式:v t= v0+ a t
从运动开始到时刻t,
那么:时间的变化量就是△t=t-0
速度的变化量就是△v=vt-v0
所以a=△v/△t =(vt-v0)/△t
于是解得:vt=v0 +at
二、匀变速直线运动速度与时间的关系式
2、讨论:
若 v 0= 0 则 v = at
物体做初速度为零的匀加速直线运动
若 a = 0 则 v = v0
物体做匀速直线运动
速度与时间的关系式
v=v0+at
矢量式
2、在具体运算中必须规定正方向!
(一般以V0的方向为正方向,则对于匀加速直线运动,加速度取正值;对于匀减速直线运动,加速度取负值)
1、适用于匀变速直线运动。
注意:
3、计算时要统一单位
4、中间时刻速度公式
×
×
×
×
甲车
t/s
v/ m·s-1
0
.
.
. .
.
.
.
.
.
.
.
1
4
3
2
5
3
12
6
9
v1
v2
t2
t1
.
.
t/s
0
1
2
3
4
V甲/m·s-1
0
3
6
9
12
a=
三、v-t 图像
匀变速直线运动的v-t 图像是一条倾斜的直线;
倾斜程度正比于加速度的大小
4
2
8
0
υ/(m·s-1)
t/s
2
4
6
8
A
4
2
8
0
υ/(m·s-1)
t/s
2
4
6
8
B
①A、B两物体开始时刻的速度分别是多少?
② A、B两物体分别做什么运动,速度是如何变化的?
③ A、B两物体加速度分别是多少,谁的速度变化快?
匀加速直线运动
匀减速直线运动
思考:
3、匀变速直线运动的 v-t图象特点:
(1)一条倾斜的直线,
(2)该直线与纵轴的交点表示t=0时刻的初速度
(3)斜率表示加速度
(2) 可以知道任一瞬时速度所对应的时刻
4、从匀变速直线运动的v-t图象可获得的物理信息:
(1) 可以知道任一时刻所对应的瞬时速度
(3)可以求运动过程的的加速度
匀变速直线运动
匀加速直线运动
速度随时间均匀增加
匀减速直线运动
速度随时间均匀减少
如:汽车启动,飞机起飞,火车出站,石头自由下落
如:汽车刹车,飞机降落,火车进站, 石头竖直上抛
5、分类:
v/m·s-1
t/s
0
5
10
15
10
20
30
40
50
v/m·s-1
t/s
0
5
10
15
10
20
30
40
50
右图是一个物体运动
的v-t图象,它的速度
怎样变化,在相等的
时间间隔内,速度的
变化量总是相等吗?
物体在做匀加速运动
吗?
0
t1
t2
t3
t4
v1
v2
v3
v4
v
t
说一说
问题1:讨论分析下面四个物体的运动有何特征?
t/s
V/m·s-1
0
物体3
t/s
V/m·s-1
0
物体2
V/m·s-1
t/s
0
物体1
V/m·s-1
t/s
0
物体4
问题2、某质点运动的v-t图象如图所示 请描述出该质点的运动情况
t/s
1
2
3
4
v/m.s-1
4
-4
0
总结:描述一个物体的运动情况可以从以下几个方面进行:
(1)初速度情况;
(2)运动性质;
(3)运动时间
例题1:
1、关于匀变速直线运动,下列说法正确的是
A、做匀变速运动的物体相等时间内速度变化相等
B、加速运动一定是匀变速运动
C、减速运动一定不是匀变速运动
D、加速度和速度方向相同时,一定是做加速运动
AD
关于匀变速直线运动的理解
例题1、某汽车正以12m/s的速度在路面上匀速行驶,前方出现紧急情况需刹车,加速度大小是3m/s2,求汽车5s末的速度。
解:以初速方向为正方向
则v=v0+at=12+(-3) ×5m/s=-3m/s
正确解法:以初速方向为正方向
当车速减为零时,v=v0+at0=12-3t0=0
解得t0=4s
即4s末汽车已刹车完毕,所以5末时汽车处于静止状态,即速度为零。
刹车问题
注意:
(与实际相符)
注意:
1、该式是矢量式(应用时要先规定正方向);
2、刹车问题要先判断停止时间。
小结:
匀变速直线运动:质点沿着一条直线,且加速度不变的运动。
分类:匀加速直线运动
匀减速直线运动
图象法:图象是一条倾斜的直线
关系式:v = v0+ at
注意运用时确定公式中矢量的正负号
Vt与t的关系
研究方法:
小结:
课外继续学习——
课本P37 “作业”4、6、7;
第二课时
矩形面积有什么物理意义?
一、匀速直线运动的位移
1、x = v t
V=5m/s
t=3s
由此可见:
对于匀速直线运动,物体的位移的大小对应着v – t 图象中一块矩形的面积。
公式法
图象法
2、x = “面积”
v0
v
t
0
问题-探究:
在匀变速直线运动中,位移与它的v-t图象是否也有类似关系?
这里的“面积”
有什么物理意义?
某同学在“探究小车的速度随时间变化的规律”的实验中,算出小车经过各计数点的瞬时速度如下表所示。
计数点序号
0
1
2
3
4
5
时间t/s
0
0.1
0.2
0.3
0.4
0.5
速度V/(m/s)
0.38
0.63
0.88
1.13
1.38
1.63
如何估测从计数点0到计数点5的位移?
思考与讨论
思考:怎样把这样的科学思想方法应用到v-t图象上?
利用v-t图象探究——匀变速直线运动的位移
t
v
v0
O
t
v
v0
O
梯形的面积就代表做匀变速直线运动物体在0(此时速度为v0)到 t(此时速度为v)这段时间的位移。
t
v
v0
O
t
t
v
v0
O
t
5
2t
5
3t
5
4t
5
t
无限分割,选取微小,化变为不变! 求和,求极限!
思维体操
一小车在水平地面上作初速度为3m/s,加速度为5m/s2的匀加速直线运动,则经过3s的时间内小车行驶的位移为多少?
若一小车在水平地面上以速度为20m/s的速度,突然急刹车以为5m/s2的加速度作减速直线运动,则经过3s的时间内小车行驶的位移为多少?
通过这个练习你的收获是……
二、匀变速直线运动的位移
由图可知:梯形OABC的面积
S = (OC+AB)×OA / 2
代入各物理量得:
又 v t= v0 + at
得
t
v
v0
O
t
vt
A
B
C
2
1
t
vt
v
S
)
(
0
+
=
2
0
2
1
at
t
v
S
+
=
平均速度:
由v-t图像得:
(1)若物体作匀加速运动,则a与 v0
(2)若物体作匀减速运动,则a与 v0
------同向
------反向
at
V/(m·s-1)
t0
t/s
o
v
v0
at 2
V0t
at
o
V/(m·s-1)
t0
v
v0
t/s
S=V0t + at2
S=V0t + (-a)t2
二、匀变速直线运动的位移与时间关系
2
0
2
1
at
t
v
S
+
=
匀变速直线运动的S-t图象是一条抛物线
注意:S-t图象不是物体运动的轨迹
做一做
位移与时间的关系也可以用图象表示,这种图象叫做位移-时间图象, 即S-t图象.运用初中数学中学到的一次函数和二次函数知识,你能画出匀变速直线运动 的S-t图象的草图吗 ?
如果一位同学问:我们研究的是直线运动,为什么画出来的s-t图象不是直线?你应该怎样向他解释?
2
at
2
1
t
0
=v
s
+
S/m
t/s
2
1
3
4
5
6
7
8
思考:物体作直线运动,为何x-t图象是曲线?
匀变速直线运动位移公式的理论推导:
由
又匀变速直线运动的平均速度:
得:
又 vt = v0 + at
得:
例:一辆汽车以1m/s2的加速度行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
先用字母代表物理量进行运算,得出用已知量表达未知量的关系式,然后再把数值代入。
这样做能够清楚地看出未知量与已知量的关系,计算也比较简便。
例2、在平直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
解决刹车问题该注意什么呢?(可别往陷阱里跳啊!)
例:汽车以12m/s速度行驶,刹车做匀减速直线运动时的加速度大小为1m/s2。
求汽车从刹车直到停止时的位移。
v = v0 + a t
速度公式:
位移公式:
v 2 – v02 = 2 a s
注意:
1、优点:不需计算时间t 。
2、公式中四个矢量 vt、v0、a、s 要规定统一的正方向。
3、若v0 = 0 ,则vt = ?
s= v0 t + a t
1
2
—
2
【例题3】龟兔赛跑是大家小时侯就听过的故事,请叙述故事梗概并画出龟兔的 s—t 图和 v—t 图。
过程分析
1.开始时,乌龟以较小的速度作匀速直线运动,兔子飞快地跑一段。
2.途中,乌龟仍以较小的速度作匀速直线运动,兔子睡起了大觉。
3.结束时,乌龟还是以较小的速度作匀速直线运动,兔子又飞快地追赶。最终还是落后于乌龟。
匀速直线运动
匀变速直线运动
位移图象
速度图象
速度图象
图象
特征
直线
直线
直线
意义
直读位移
直读速度
直读速度
纵轴截距
初始位置
速度
初速度
斜率
速度
×
加速度
面积
×
位移
位移
直线运动图象信息的比较
小结
1、速度公式:
2、位移公式:
3、速度—位移公式:
x = v0 t + a t
1
2
—
2
v = v0 + a t
v 2 – v02 = 2 a x
(不涉及 x )
(不涉及 v )
(不涉及 t )
x = (v0 +vt) t
1
2
—
(不涉及 a )
例:已知汽车刹车后10s停下来,且汽车在匀减速直线运动时的加速度大小为1m/s2。
求汽车停止前最后1s内的位移。
末速度为零的匀减速直线运动可看成初速度为零,加速度大小相等的匀加速直线运动。
v0
A
B
0
a
a
附:解题技巧1
附:解题技巧2
某物体从静止开始做匀加速直线运动,经过4s达到2m/s,然后以这个速度运动12s最后做匀减速直线运动,经过4s停下来。求物体运动的距离
由v-t图像得
s = 1/2( 12+20 )×2 = 32 m
2
v/m/s
0
t/s
4 8 12 16 20
课外继续学习——
1、完成课本P37 “作业”2、3、5;
2、练习册第三章第一节练习。
谢 谢
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
