人教版(2019)高中物理 选择性必修第三册 第1章 章末综合提升学案
文档属性
| 名称 | 人教版(2019)高中物理 选择性必修第三册 第1章 章末综合提升学案 | 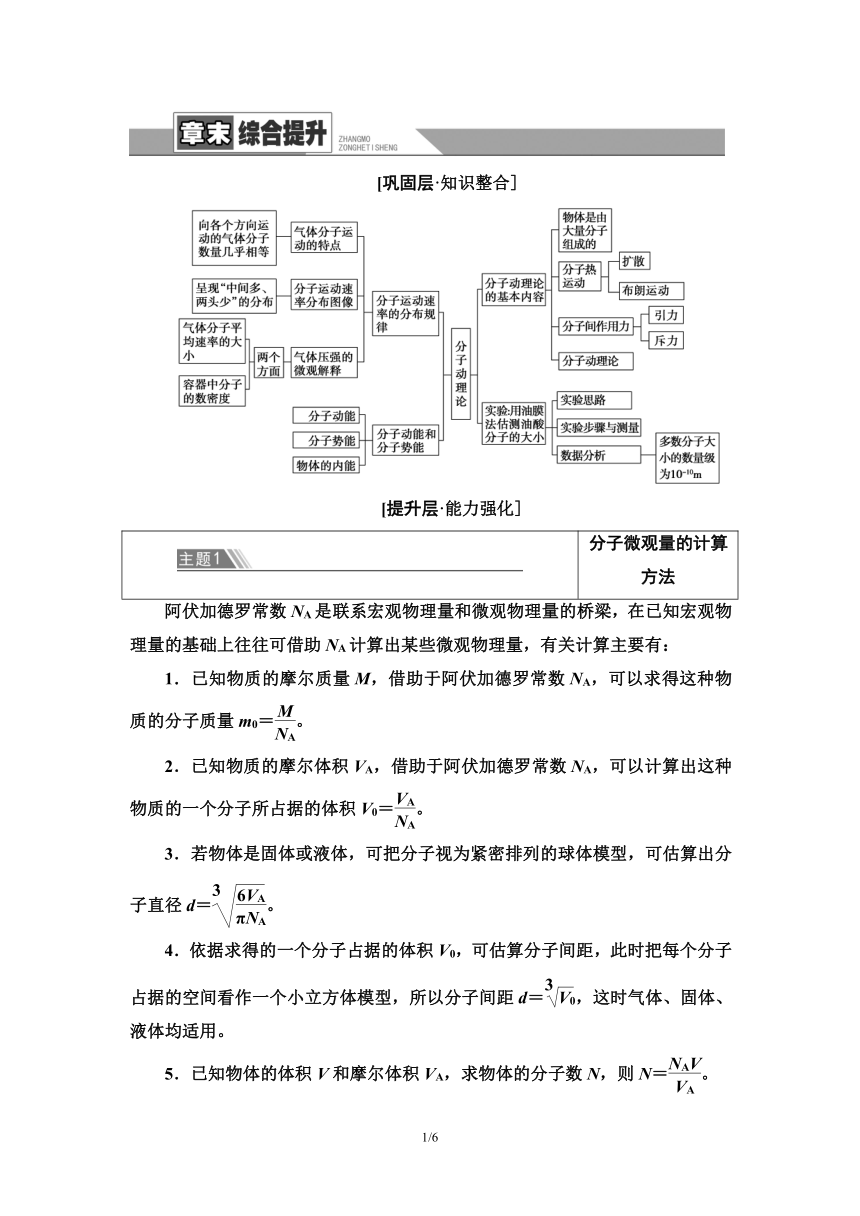 | |
| 格式 | doc | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-17 17:44:23 | ||
图片预览



文档简介
[巩固层·知识整合]
[提升层·能力强化]
分子微观量的计算方法
阿伏加德罗常数NA是联系宏观物理量和微观物理量的桥梁,在已知宏观物理量的基础上往往可借助NA计算出某些微观物理量,有关计算主要有:
1.已知物质的摩尔质量M,借助于阿伏加德罗常数NA,可以求得这种物质的分子质量m0=。
2.已知物质的摩尔体积VA,借助于阿伏加德罗常数NA,可以计算出这种物质的一个分子所占据的体积V0=。
3.若物体是固体或液体,可把分子视为紧密排列的球体模型,可估算出分子直径d=。
4.依据求得的一个分子占据的体积V0,可估算分子间距,此时把每个分子占据的空间看作一个小立方体模型,所以分子间距d=,这时气体、固体、液体均适用。
5.已知物体的体积V和摩尔体积VA,求物体的分子数N,则N=。
6.已知物体的质量m和摩尔质量M,求物体的分子数N,则N=NA。
【例1】 已知水的密度ρ=1.0×103 kg/m3,水的摩尔质量M=1.8×10-2 kg/mol。求:
(1)1 g水中所含水分子数目;
(2)水分子的质量;
(3)水分子的直径。(保留两位有效数字)
[解析] (1)因为1 mol任何物质中含有分子数都是NA,所以只要知道了1 g水的物质的量n,就可求得其分子总数N。
N=nNA=NA=×6.02×1023个=3.3×1022个。
(2)水分子质量
m0== kg=3.0×10-26 kg。
(3)水的摩尔体积V=,设水分子是一个挨一个紧密排列的,则一个水分子的体积V0==。将水分子视为球形,则V0=πd3,即
πd3=
解得d== m=3.9×10-10 m。
[答案] (1)3.3×1022个 (2)3.0×10-26 kg (3)3.9×10-10 m
[一语通关]
分子动理论中宏观量与微观量之间的关系
由宏观量计算微观量,或由微观量计算宏观量,都要通过阿伏加德罗常数建立联系。所以说,阿伏加德罗常数是联系宏观量与微观量的桥梁。
用油膜法估测分子的大小
用油膜法估测分子直径的实验原理是:油酸是一种脂肪酸,它的分子的一部分和水分子的亲和力很强。当把一滴用酒精稀释过的油酸滴在水面上时,酒精溶于水或挥发,在水面上形成一层油酸薄膜,薄膜可认为是单分子油膜,如图所示。将水面上形成的油膜形状画到坐标纸上,可以计算出油膜的面积,根据纯油酸的体积V和油膜的面积S,可以计算出油膜的厚度d=,即油酸分子的直径。
【例2】 “用油膜法估测分子的大小”的实验的方法及步骤如下:
①向体积V油=1 mL的油酸中加酒精,直至总量达到V总=500 mL;
②用注射器吸取①中配制好的油酸酒精溶液,把它一滴一滴地滴入小量筒中,当滴入n=100滴时,测得其体积恰好是V0=1 mL;
③先往边长为30~40 cm的浅盘里倒入2 cm深的水,然后将________均匀地撒在水面上;
④用注射器往水面上滴一滴油酸酒精溶液,待油酸薄膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描下油酸膜的形状;
⑤将画有油酸膜轮廓的玻璃板放在坐标纸上,如图所示,数出轮廓范围内小方格的个数N,小方格的边长l=20 mm。根据以上信息,回答下列问题:
(1)步骤③中应填写:_____________________________。
(2)1滴油酸酒精溶液中纯油酸的体积V′是___________ mL。
(3)油酸分子直径是________ m。
[解析] (1)为了显示单分子油膜的形状,需要在水面上撒爽身粉。
(2)1滴油酸酒精溶液中纯油酸的体积
V′==× mL=2×10-5 mL。
(3)根据大于半个方格的算一个,小于半个方格的舍去,油膜形状占据方格数大约为115个,故面积
S=115×20×20 mm2=4.6×104 mm2
油酸分子直径d== mm≈4.3×10-7 mm=4.3×10-10 m。
[答案] (1)爽身粉 (2)2×10-5 (3)4.3×10-10
[一语通关]
油膜法估测分子直径,关键是获得一滴油酸酒精溶液的体积,并由配制浓度求出其中所含纯油酸的体积,再就是用数格数法(对外围小格采用“填补法”即“四舍五入”法)求出油膜面积,再由公式d=计算结果。
分子力、分子势能和物体的内能
1.分子力是分子引力和分子斥力的合力,分子势能是由分子间的分子力和分子间的相对位置决定的能, 分子力F和分子势能Ep都与分子间的距离有关,二者随分子间距离r变化的关系如图所示。
(1)分子间同时存在着引力和斥力,它们都随分子间距离的增大(减小)而减小(增大),但斥力比引力变化得快。
(2)在r(3)在r>r0的范围内,随着分子间距离的增大,分子力F先增大后减小,而分子势能Ep一直增大。
(4)当r=r0时,分子力F为零,分子势能Ep最小,但不一定等于零。
2.内能是物体中所有分子热运动动能与分子势能的总和。温度升高时,物体分子的平均动能增加;体积变化时,分子势能变化。内能也与物体的物态有关。
解答有关“内能”的题目,应把握以下四点:
(1)温度是分子平均动能的标志,而不是分子平均速率的标志。
(2)当分子间距离发生变化时,若分子力做正功,则分子势能减小;若分子力做负功,则分子势能增加。
(3)内能是物体内所有分子动能与分子势能的总和,它宏观上取决于物质的量、温度、体积及物态。
(4)理想气体就是分子间没有相互作用力的气体,这是一种理想模型。理想气体无分子势能变化,因此一定质量理想气体的内能的变化只与温度有关。
【例3】 如图所示,甲分子固定在坐标原点O,乙分子位于x轴上,甲分子对乙分子的作用力与两分子间距离的关系如图中曲线所示,F>0为斥力,F<0为引力,a、b、c、d为x轴上四个特定的位置,现把乙分子从a处由静止释放,若规定无限远处分子势能为零,则下列说法正确的是( )
A.乙分子在b处势能最小,且势能为负值
B.乙分子在c处势能最小,且势能为负值
C.乙分子在d处势能一定为正值
D.乙分子在d处势能一定小于在a处势能
B [由于乙分子由静止释放,在ac间一直受到甲分子的引力而做加速运动,引力做正功,分子势能一直在减小,到达c点时所受分子力为零,加速度为零,速度最大,动能最大,分子势能最小,为负值。由于惯性,到达c点后乙分子继续向甲分子靠近,由于分子力为斥力,故乙分子做减速运动,直到速度减为零,设到达d点后返回,故乙分子运动范围在ad之间。在分子力表现为斥力的那一段cd上,随分子间距的减小,乙分子克服斥力做功,分子力、分子势能随间距的减小一直增加。故B正确,A、C、D错误。]
[一语通关]
(1)当r=r0时,分子力F为零,分子势能最小为负值。
(2)分子热运动:分子做永不停息的无规则运动,温度越高越剧烈,大量分子的运动符合统计规律,例如,温度升高,分子的平均动能增加,单个分子的运动无规律也没有实际意义。
[培养层·素养升华]
如图所示为某实验器材的结构示意图,金属内筒和隔热外筒间封闭一定体积的气体,内筒中有水,在水加热升温的过程中(忽略液体和气体的体积变化)。
[设问探究]
1.气体分子间引力、斥力怎样变化?
2.是不是所有气体分子运动速率都增大了?
3.气体的内能怎样变化?
提示:1.封闭气体分子数与体积不变,所以分子间平均距离不变,所以分子间斥力与引力都不变,分子势能也不变。
2.不是。封闭气体温度升高,分子热运动平均动能增大,分子热运动平均速率增大,并不是所有分子速率都增大。
3.气体的分子势能没有变,平均动能增大,所以气体的内能增大。
[深度思考]
(多选)下列叙述正确的是( )
A.若分子间距离r=r0时,两分子间分子力F=0,则当两分子间距离由小于r0逐渐增大到10r0过程中,分子间相互作用的势能先减小后增大
B.对一定质量气体加热,其内能一定增加
C.物体的温度越高,其分子的平均动能越大
D.布朗运动就是液体分子的热运动
AC [当r6/6
[提升层·能力强化]
分子微观量的计算方法
阿伏加德罗常数NA是联系宏观物理量和微观物理量的桥梁,在已知宏观物理量的基础上往往可借助NA计算出某些微观物理量,有关计算主要有:
1.已知物质的摩尔质量M,借助于阿伏加德罗常数NA,可以求得这种物质的分子质量m0=。
2.已知物质的摩尔体积VA,借助于阿伏加德罗常数NA,可以计算出这种物质的一个分子所占据的体积V0=。
3.若物体是固体或液体,可把分子视为紧密排列的球体模型,可估算出分子直径d=。
4.依据求得的一个分子占据的体积V0,可估算分子间距,此时把每个分子占据的空间看作一个小立方体模型,所以分子间距d=,这时气体、固体、液体均适用。
5.已知物体的体积V和摩尔体积VA,求物体的分子数N,则N=。
6.已知物体的质量m和摩尔质量M,求物体的分子数N,则N=NA。
【例1】 已知水的密度ρ=1.0×103 kg/m3,水的摩尔质量M=1.8×10-2 kg/mol。求:
(1)1 g水中所含水分子数目;
(2)水分子的质量;
(3)水分子的直径。(保留两位有效数字)
[解析] (1)因为1 mol任何物质中含有分子数都是NA,所以只要知道了1 g水的物质的量n,就可求得其分子总数N。
N=nNA=NA=×6.02×1023个=3.3×1022个。
(2)水分子质量
m0== kg=3.0×10-26 kg。
(3)水的摩尔体积V=,设水分子是一个挨一个紧密排列的,则一个水分子的体积V0==。将水分子视为球形,则V0=πd3,即
πd3=
解得d== m=3.9×10-10 m。
[答案] (1)3.3×1022个 (2)3.0×10-26 kg (3)3.9×10-10 m
[一语通关]
分子动理论中宏观量与微观量之间的关系
由宏观量计算微观量,或由微观量计算宏观量,都要通过阿伏加德罗常数建立联系。所以说,阿伏加德罗常数是联系宏观量与微观量的桥梁。
用油膜法估测分子的大小
用油膜法估测分子直径的实验原理是:油酸是一种脂肪酸,它的分子的一部分和水分子的亲和力很强。当把一滴用酒精稀释过的油酸滴在水面上时,酒精溶于水或挥发,在水面上形成一层油酸薄膜,薄膜可认为是单分子油膜,如图所示。将水面上形成的油膜形状画到坐标纸上,可以计算出油膜的面积,根据纯油酸的体积V和油膜的面积S,可以计算出油膜的厚度d=,即油酸分子的直径。
【例2】 “用油膜法估测分子的大小”的实验的方法及步骤如下:
①向体积V油=1 mL的油酸中加酒精,直至总量达到V总=500 mL;
②用注射器吸取①中配制好的油酸酒精溶液,把它一滴一滴地滴入小量筒中,当滴入n=100滴时,测得其体积恰好是V0=1 mL;
③先往边长为30~40 cm的浅盘里倒入2 cm深的水,然后将________均匀地撒在水面上;
④用注射器往水面上滴一滴油酸酒精溶液,待油酸薄膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描下油酸膜的形状;
⑤将画有油酸膜轮廓的玻璃板放在坐标纸上,如图所示,数出轮廓范围内小方格的个数N,小方格的边长l=20 mm。根据以上信息,回答下列问题:
(1)步骤③中应填写:_____________________________。
(2)1滴油酸酒精溶液中纯油酸的体积V′是___________ mL。
(3)油酸分子直径是________ m。
[解析] (1)为了显示单分子油膜的形状,需要在水面上撒爽身粉。
(2)1滴油酸酒精溶液中纯油酸的体积
V′==× mL=2×10-5 mL。
(3)根据大于半个方格的算一个,小于半个方格的舍去,油膜形状占据方格数大约为115个,故面积
S=115×20×20 mm2=4.6×104 mm2
油酸分子直径d== mm≈4.3×10-7 mm=4.3×10-10 m。
[答案] (1)爽身粉 (2)2×10-5 (3)4.3×10-10
[一语通关]
油膜法估测分子直径,关键是获得一滴油酸酒精溶液的体积,并由配制浓度求出其中所含纯油酸的体积,再就是用数格数法(对外围小格采用“填补法”即“四舍五入”法)求出油膜面积,再由公式d=计算结果。
分子力、分子势能和物体的内能
1.分子力是分子引力和分子斥力的合力,分子势能是由分子间的分子力和分子间的相对位置决定的能, 分子力F和分子势能Ep都与分子间的距离有关,二者随分子间距离r变化的关系如图所示。
(1)分子间同时存在着引力和斥力,它们都随分子间距离的增大(减小)而减小(增大),但斥力比引力变化得快。
(2)在r
(4)当r=r0时,分子力F为零,分子势能Ep最小,但不一定等于零。
2.内能是物体中所有分子热运动动能与分子势能的总和。温度升高时,物体分子的平均动能增加;体积变化时,分子势能变化。内能也与物体的物态有关。
解答有关“内能”的题目,应把握以下四点:
(1)温度是分子平均动能的标志,而不是分子平均速率的标志。
(2)当分子间距离发生变化时,若分子力做正功,则分子势能减小;若分子力做负功,则分子势能增加。
(3)内能是物体内所有分子动能与分子势能的总和,它宏观上取决于物质的量、温度、体积及物态。
(4)理想气体就是分子间没有相互作用力的气体,这是一种理想模型。理想气体无分子势能变化,因此一定质量理想气体的内能的变化只与温度有关。
【例3】 如图所示,甲分子固定在坐标原点O,乙分子位于x轴上,甲分子对乙分子的作用力与两分子间距离的关系如图中曲线所示,F>0为斥力,F<0为引力,a、b、c、d为x轴上四个特定的位置,现把乙分子从a处由静止释放,若规定无限远处分子势能为零,则下列说法正确的是( )
A.乙分子在b处势能最小,且势能为负值
B.乙分子在c处势能最小,且势能为负值
C.乙分子在d处势能一定为正值
D.乙分子在d处势能一定小于在a处势能
B [由于乙分子由静止释放,在ac间一直受到甲分子的引力而做加速运动,引力做正功,分子势能一直在减小,到达c点时所受分子力为零,加速度为零,速度最大,动能最大,分子势能最小,为负值。由于惯性,到达c点后乙分子继续向甲分子靠近,由于分子力为斥力,故乙分子做减速运动,直到速度减为零,设到达d点后返回,故乙分子运动范围在ad之间。在分子力表现为斥力的那一段cd上,随分子间距的减小,乙分子克服斥力做功,分子力、分子势能随间距的减小一直增加。故B正确,A、C、D错误。]
[一语通关]
(1)当r=r0时,分子力F为零,分子势能最小为负值。
(2)分子热运动:分子做永不停息的无规则运动,温度越高越剧烈,大量分子的运动符合统计规律,例如,温度升高,分子的平均动能增加,单个分子的运动无规律也没有实际意义。
[培养层·素养升华]
如图所示为某实验器材的结构示意图,金属内筒和隔热外筒间封闭一定体积的气体,内筒中有水,在水加热升温的过程中(忽略液体和气体的体积变化)。
[设问探究]
1.气体分子间引力、斥力怎样变化?
2.是不是所有气体分子运动速率都增大了?
3.气体的内能怎样变化?
提示:1.封闭气体分子数与体积不变,所以分子间平均距离不变,所以分子间斥力与引力都不变,分子势能也不变。
2.不是。封闭气体温度升高,分子热运动平均动能增大,分子热运动平均速率增大,并不是所有分子速率都增大。
3.气体的分子势能没有变,平均动能增大,所以气体的内能增大。
[深度思考]
(多选)下列叙述正确的是( )
A.若分子间距离r=r0时,两分子间分子力F=0,则当两分子间距离由小于r0逐渐增大到10r0过程中,分子间相互作用的势能先减小后增大
B.对一定质量气体加热,其内能一定增加
C.物体的温度越高,其分子的平均动能越大
D.布朗运动就是液体分子的热运动
AC [当r
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
