8.2 幂的乘方(第1课时 ) 优质课件(共23张PPT)
文档属性
| 名称 | 8.2 幂的乘方(第1课时 ) 优质课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览








文档简介
第八章 整式的乘法
8.2 幂的乘方与积的乘方
七年级数学下册冀教版
第1课时 幂的乘方
1
幂的乘方
CONTENTS
1
新知导入
想一想:
地球、木星、太阳可以近似地看做是球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
V球= —πr3 ,
其中V是球的体积,r是球的半径.
3
4
103倍
(102)3倍
CONTENTS
2
课程讲授
幂的乘方
问题1
依据同底数幂乘法的性质,210×210×210= .
根据乘方的意义,210×210×210可以表示为 .
由此,能得到什么结论?
230
(210)3
230=(210)3
幂的乘方
问题2.1
(102)3代表什么意义?
3个102相乘,102×102×102
问题2.2
(102)3=10( )
(102)3=102×102×102
=102+2+2
=102×3
=106
6
幂的乘方
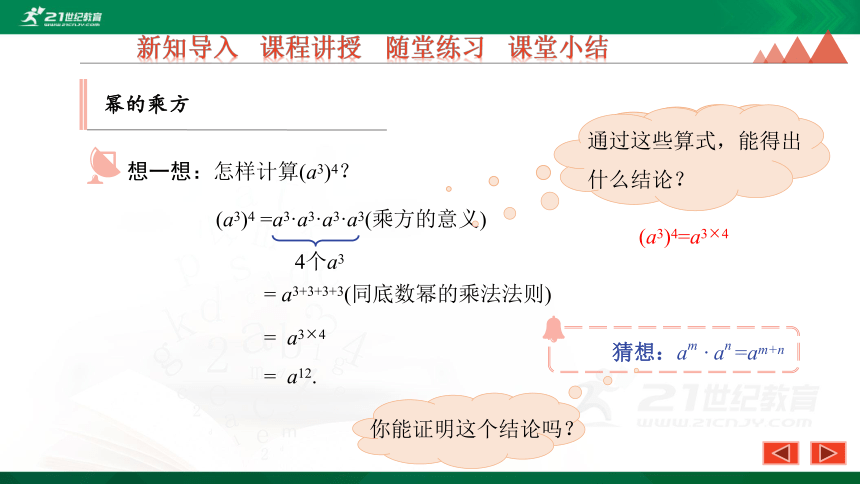
想一想:怎样计算(a3)4?
(a3)4 =a3·a3·a3·a3(乘方的意义)
4个a3
= a3+3+3+3(同底数幂的乘法法则)
= a3×4
= a12.
你有什么发现?
(a3)4=a3×4
通过这些算式,能得出什么结论?
猜想:am · an =am+n
你能证明这个结论吗?
幂的乘方
(am)n = am · am · … · am
= am+m+…+m
= amn(m,n都是正整数)
n个am
n个m
(幂的意义)
(同底数幂的乘法性质)
幂的乘方
归纳:幂的乘方法则:
( am ) n = a mn (m,n是正整数).
幂的乘方,底数不变,指数相乘.
例1 计算:
幂的乘方
(1) (103)4; (2) (c2)3; (3) (a4)m.
解:(1) (103)4=103×4=1012;
(2) (c2)3=c2×3=c6;
(3) (a4)m=a4×m=a4m.
幂的乘方
例2 计算:
(1) x? (x2)3; (2) a?a2?a3-(a2)3.
解:(1) x? (x2)3= x? x2×3=x? x6=x7;
(2) a?a2?a3-(a2)3= a1+2+3-a2×3=a6-a6=0.
提示:先算乘方,再算乘法,最后算加减.
幂的乘方
想一想:同底数幂的乘法和幂的乘方有什么共同点和不同点?
1.从底数看:底数不变. (共同点)
2.从指数看:
同底数幂的乘法,指数相加
幂的乘方,指数相乘
(不同点)
(2)幂的乘方,底数不变,指数相乘
(1)同底数幂相乘,底数不变,指数相加
( am ) n = a mn (m,n是正整数).
am·an = a m+n (m,n是正整数).
幂的乘方
练一练:计算:
= b5×5
= b25 ;
(b5)5
解:(1)
= an×3
= a3n ;
(2)
(an)3
(1) (b5)5;
(2) (an)3;
(3) -(x2)m;
(4) (y2)3 · y;
(5) 2(a2)6 -(a3)4.
= -x2×m
= -x2m ;
(3)
-(x2)m
= y2×3 · y
= y6 · y
= y7;
(4)
(y2)3 · y
=2a2×6 -a3×4
=2a12-a12
=a12.
(5)
2(a2)6 – (a3)4
CONTENTS
3
随堂练习
1.下列计算中,错误的是( )
A.[(a+b)2]3=(a+b)6
B.[(a+b)2]5=(a+b)7
C.[(a-b)3]n=(a-b)3n
D.[(a-b)3]2=(a-b)6
2.若x,y互为相反数,则(5x)2·(52)y+1的值为_______.
B
25
3.计算(-x5)4+(-x4)5的结果是( )
A.0 B.2x20
C.-2x20 D.x40
4.若3×9m×27m=321,则m的值为( )
A.3 B.4
C.5 D.6
B
A
5.计算:
(1)5(a3)4-11(a6)2;
(3)[(a+b)3]4+[-(a+b)2]6.
(2)7x4·x5·(-x)7+5(x4)4-(x8)2;
解:5(a3)4-11(a6)2
=5a12-11a12
=-6a12.
解:7x4·x5·(-x)7+5(x4)4-(x8)2
=-7x9·x7+5x16-x16
=-3x16.
解:[(a+b)3]4+[-(a+b)2]6
=(a+b)12-(a+b)12
=0.
6.(1)已知ax=2,ay=3,求a2x+2y的值;
(2)若42a+1=64,解关于x的方程2ax+3=5.
解:(1)∵ax=2,ay=3,
∴ax·ay=2×3,
∴ax+y=6,a2x+2y=62=36.
(2)∵42a+1=64,
∴42a+1=43,
∴2a+1=3,
∴a=1,
∴2ax+3=5化为2x+3=5,
x=1.
CONTENTS
4
课堂小结
幂的乘方
法则
(am)n=amn (m,n都是正整数)
对比
幂的乘方,底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别:(am)n=amn;am ﹒an=am+n
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
8.2 幂的乘方与积的乘方
七年级数学下册冀教版
第1课时 幂的乘方
1
幂的乘方
CONTENTS
1
新知导入
想一想:
地球、木星、太阳可以近似地看做是球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
V球= —πr3 ,
其中V是球的体积,r是球的半径.
3
4
103倍
(102)3倍
CONTENTS
2
课程讲授
幂的乘方
问题1
依据同底数幂乘法的性质,210×210×210= .
根据乘方的意义,210×210×210可以表示为 .
由此,能得到什么结论?
230
(210)3
230=(210)3
幂的乘方
问题2.1
(102)3代表什么意义?
3个102相乘,102×102×102
问题2.2
(102)3=10( )
(102)3=102×102×102
=102+2+2
=102×3
=106
6
幂的乘方
想一想:怎样计算(a3)4?
(a3)4 =a3·a3·a3·a3(乘方的意义)
4个a3
= a3+3+3+3(同底数幂的乘法法则)
= a3×4
= a12.
你有什么发现?
(a3)4=a3×4
通过这些算式,能得出什么结论?
猜想:am · an =am+n
你能证明这个结论吗?
幂的乘方
(am)n = am · am · … · am
= am+m+…+m
= amn(m,n都是正整数)
n个am
n个m
(幂的意义)
(同底数幂的乘法性质)
幂的乘方
归纳:幂的乘方法则:
( am ) n = a mn (m,n是正整数).
幂的乘方,底数不变,指数相乘.
例1 计算:
幂的乘方
(1) (103)4; (2) (c2)3; (3) (a4)m.
解:(1) (103)4=103×4=1012;
(2) (c2)3=c2×3=c6;
(3) (a4)m=a4×m=a4m.
幂的乘方
例2 计算:
(1) x? (x2)3; (2) a?a2?a3-(a2)3.
解:(1) x? (x2)3= x? x2×3=x? x6=x7;
(2) a?a2?a3-(a2)3= a1+2+3-a2×3=a6-a6=0.
提示:先算乘方,再算乘法,最后算加减.
幂的乘方
想一想:同底数幂的乘法和幂的乘方有什么共同点和不同点?
1.从底数看:底数不变. (共同点)
2.从指数看:
同底数幂的乘法,指数相加
幂的乘方,指数相乘
(不同点)
(2)幂的乘方,底数不变,指数相乘
(1)同底数幂相乘,底数不变,指数相加
( am ) n = a mn (m,n是正整数).
am·an = a m+n (m,n是正整数).
幂的乘方
练一练:计算:
= b5×5
= b25 ;
(b5)5
解:(1)
= an×3
= a3n ;
(2)
(an)3
(1) (b5)5;
(2) (an)3;
(3) -(x2)m;
(4) (y2)3 · y;
(5) 2(a2)6 -(a3)4.
= -x2×m
= -x2m ;
(3)
-(x2)m
= y2×3 · y
= y6 · y
= y7;
(4)
(y2)3 · y
=2a2×6 -a3×4
=2a12-a12
=a12.
(5)
2(a2)6 – (a3)4
CONTENTS
3
随堂练习
1.下列计算中,错误的是( )
A.[(a+b)2]3=(a+b)6
B.[(a+b)2]5=(a+b)7
C.[(a-b)3]n=(a-b)3n
D.[(a-b)3]2=(a-b)6
2.若x,y互为相反数,则(5x)2·(52)y+1的值为_______.
B
25
3.计算(-x5)4+(-x4)5的结果是( )
A.0 B.2x20
C.-2x20 D.x40
4.若3×9m×27m=321,则m的值为( )
A.3 B.4
C.5 D.6
B
A
5.计算:
(1)5(a3)4-11(a6)2;
(3)[(a+b)3]4+[-(a+b)2]6.
(2)7x4·x5·(-x)7+5(x4)4-(x8)2;
解:5(a3)4-11(a6)2
=5a12-11a12
=-6a12.
解:7x4·x5·(-x)7+5(x4)4-(x8)2
=-7x9·x7+5x16-x16
=-3x16.
解:[(a+b)3]4+[-(a+b)2]6
=(a+b)12-(a+b)12
=0.
6.(1)已知ax=2,ay=3,求a2x+2y的值;
(2)若42a+1=64,解关于x的方程2ax+3=5.
解:(1)∵ax=2,ay=3,
∴ax·ay=2×3,
∴ax+y=6,a2x+2y=62=36.
(2)∵42a+1=64,
∴42a+1=43,
∴2a+1=3,
∴a=1,
∴2ax+3=5化为2x+3=5,
x=1.
CONTENTS
4
课堂小结
幂的乘方
法则
(am)n=amn (m,n都是正整数)
对比
幂的乘方,底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别:(am)n=amn;am ﹒an=am+n
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
