8.5 平方差公式(第1课时) 优质课件(共22张PPT)
文档属性
| 名称 | 8.5 平方差公式(第1课时) 优质课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览







文档简介
第八章 整式的乘法
8.5 乘法公式
七年级数学下册冀教版
第1课时 平方差公式
1
平方差公式
CONTENTS
1
新知导入
(a+b)(m+n)
=___(m+n)+___(m+n)
=___+___+___+___
想一想:
根据所学知识,完成下面内容
b
a
=___(m+n)-___(m+n)
=___+___-___-___
(a+b)(m-n)
b
a
am
an
bm
bn
am
an
bm
bn
CONTENTS
2
课程讲授
平方差公式
问题1
计算:
(1)(x+1)(x-1)= .
(2) (a+2)(a-2)= .
(3) (2x+1)(2x-1)= .
(4) (a+b)(a-b)= .
x2 - 1
a2-4
4x2 - 1
a2-b2
上面四个式子中,两个乘式之间有什么特点?
两个数的和
这两个数的差
乘积合并同类项后的多项式有什么特点?
x2 - 12
a2-22
(2x)2 - 12
两数平方的差
平方差公式
归纳:平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
平方差公式
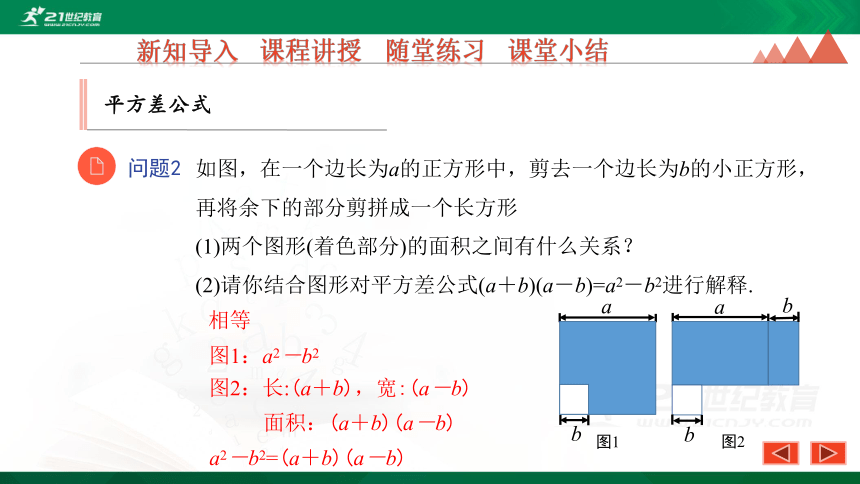
问题2
如图,在一个边长为a的正方形中,剪去一个边长为b的小正方形,再将余下的部分剪拼成一个长方形
(1)两个图形(着色部分)的面积之间有什么关系?
(2)请你结合图形对平方差公式(a+b)(a-b)=a2-b2进行解释.
b
a
图1
相等
图1:a2-b2
图2:长:(a+b),宽:(a-b)
面积:(a+b)(a-b)
b
a
图2
b
a2-b2=(a+b)(a-b)
平方差公式
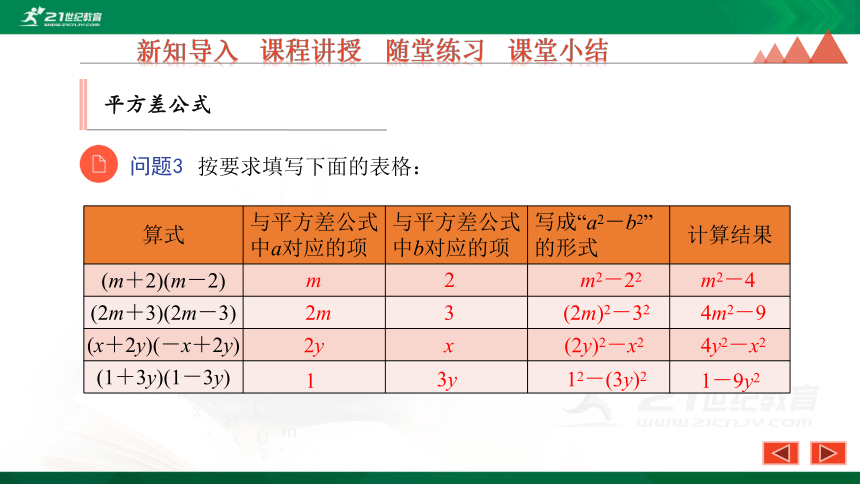
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}算式
与平方差公式中a对应的项
与平方差公式中b对应的项
写成“a2-b2”的形式
计算结果
(m+2)(m-2)
(2m+3)(2m-3)
(x+2y)(-x+2y)
(1+3y)(1-3y)
问题3
按要求填写下面的表格:
m
2
m2-22
m2-4
2m
3
(2m)2-32
4m2-9
2y
x
(2y)2-x2
4y2-x2
1
3y
12-(3y)2
1-9y2
平方差公式
想一想:判断式子(5a﹣7b)(﹣5a﹣7b)能否用平方差公式进行计算?如果能,请计算出结果.
(a + b)(a - b)
相同的项
互为相反的项
(5a-7b)(-5a-7b)
相同的项
互为相反的项
=(-7b+5a)( -7b - 5a)
加
减
负
负
=(-7b)2-(5a)2
=49b2-25a2
平方差公式
归纳:判断两个多项式相乘能否用平方差公式进行计算的方法:
1. 判断时要把两个多项式中每项前的符号都看成性质符号,如果两个多项式中既有相同的项,又有互为相反的项,则一定能用平方差公式进行计算.这时要把相同的项写在每个多项式的第一项,互为相反的项写在第二项,这样就写成了(a+b)(a-b)的形式.
2. 利用平方差公式计算时,每个多项式中两项之间的符号看成运算符号,首项前如果有符号则看成性质符号
平方差公式
练一练:判断下列各题哪些能用平方差公式进行计算?
(1) (3x-2y)(3y+2x) (2)(3a+4b)(4b-3a)
(3) (-a2 - b2)(-a2 +b2) (4) (2m-3n)(-2m-3n)
(5) (a-b)( -b-a) (6) (x+2y)(-2y+x)
(7) (-3a3+4b2)(-4b2-3a3) (8) (a-2b)(2b-a)
例 计算:(1)(2x+y)(2x-y); (2)( x+5y)( x-5y);
平方差公式
解:(1)
(2x+y)(2x-y)
=(2x)2-y2
=4x2-y2.
(2)
(3)(-5a+3b)(-5a-3b).
(3)
(-5a+3b)(-5a-3b)
=(-5a)2-(3b)2
=25a2-9b2.
CONTENTS
3
随堂练习
1.计算(2x+3)(2x-3)的值是( )
A.4x2-9 B.4x2-3
C.2x2-9 D.2x2-3
2.已知a=7202,b=719×721,则( )
A.a=b B.a>b
C.a<b D.a≤b
A
A
3.已知(-3a+m)(4b+n)=16b2-9a2,则m,n的值分别为( )
A.m=-4b,n=3a
B.m=4b,n=-3a
C.m=4b,n=3a
D.m=3a,n=4b
4.计算:
(1)(x+1)(x-____)=x2-1;
(2)(x+3y)______=9y2-x2.
C
(3y-x)
1
5.运用平方差公式计算:
(1)(m+1)(m-1)(m2+1); (2)503×497;
(3) (x-y)(x+y)(x2+y2)(x4+y4).
解:(m+1)(m-1)(m2+1)
=(m2-1)(m2+1).
=m4-1
=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
解:(x-y)(x+y)(x2+y2)(x4+y4)
=249991
解:503×497
=(500+3)(500-3)
=5002-32
6.某公园原有长方形绿地一块,现进行如下改造,将长减少2 m,将宽增加2 m,改造后得到一块正方形绿地,它的面积是原绿地面积的2倍,求改造后正方形绿地的面积.
解:设改造后正方形绿地的边长为x m,
则改造前的长是(x+2) m,宽是(x-2) m.
根据题意,有2(x+2)(x-2)=x2,
即2(x2-4)=x2,
可得x2=8.
答:改造后正方形绿地的面积为8 m2.
CONTENTS
4
课堂小结
平方差公式
内容
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
运用
只有符合公式条件的乘法,才能运用公式简化运算,其余运算仍按乘法法则进行
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
8.5 乘法公式
七年级数学下册冀教版
第1课时 平方差公式
1
平方差公式
CONTENTS
1
新知导入
(a+b)(m+n)
=___(m+n)+___(m+n)
=___+___+___+___
想一想:
根据所学知识,完成下面内容
b
a
=___(m+n)-___(m+n)
=___+___-___-___
(a+b)(m-n)
b
a
am
an
bm
bn
am
an
bm
bn
CONTENTS
2
课程讲授
平方差公式
问题1
计算:
(1)(x+1)(x-1)= .
(2) (a+2)(a-2)= .
(3) (2x+1)(2x-1)= .
(4) (a+b)(a-b)= .
x2 - 1
a2-4
4x2 - 1
a2-b2
上面四个式子中,两个乘式之间有什么特点?
两个数的和
这两个数的差
乘积合并同类项后的多项式有什么特点?
x2 - 12
a2-22
(2x)2 - 12
两数平方的差
平方差公式
归纳:平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
平方差公式
问题2
如图,在一个边长为a的正方形中,剪去一个边长为b的小正方形,再将余下的部分剪拼成一个长方形
(1)两个图形(着色部分)的面积之间有什么关系?
(2)请你结合图形对平方差公式(a+b)(a-b)=a2-b2进行解释.
b
a
图1
相等
图1:a2-b2
图2:长:(a+b),宽:(a-b)
面积:(a+b)(a-b)
b
a
图2
b
a2-b2=(a+b)(a-b)
平方差公式
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}算式
与平方差公式中a对应的项
与平方差公式中b对应的项
写成“a2-b2”的形式
计算结果
(m+2)(m-2)
(2m+3)(2m-3)
(x+2y)(-x+2y)
(1+3y)(1-3y)
问题3
按要求填写下面的表格:
m
2
m2-22
m2-4
2m
3
(2m)2-32
4m2-9
2y
x
(2y)2-x2
4y2-x2
1
3y
12-(3y)2
1-9y2
平方差公式
想一想:判断式子(5a﹣7b)(﹣5a﹣7b)能否用平方差公式进行计算?如果能,请计算出结果.
(a + b)(a - b)
相同的项
互为相反的项
(5a-7b)(-5a-7b)
相同的项
互为相反的项
=(-7b+5a)( -7b - 5a)
加
减
负
负
=(-7b)2-(5a)2
=49b2-25a2
平方差公式
归纳:判断两个多项式相乘能否用平方差公式进行计算的方法:
1. 判断时要把两个多项式中每项前的符号都看成性质符号,如果两个多项式中既有相同的项,又有互为相反的项,则一定能用平方差公式进行计算.这时要把相同的项写在每个多项式的第一项,互为相反的项写在第二项,这样就写成了(a+b)(a-b)的形式.
2. 利用平方差公式计算时,每个多项式中两项之间的符号看成运算符号,首项前如果有符号则看成性质符号
平方差公式
练一练:判断下列各题哪些能用平方差公式进行计算?
(1) (3x-2y)(3y+2x) (2)(3a+4b)(4b-3a)
(3) (-a2 - b2)(-a2 +b2) (4) (2m-3n)(-2m-3n)
(5) (a-b)( -b-a) (6) (x+2y)(-2y+x)
(7) (-3a3+4b2)(-4b2-3a3) (8) (a-2b)(2b-a)
例 计算:(1)(2x+y)(2x-y); (2)( x+5y)( x-5y);
平方差公式
解:(1)
(2x+y)(2x-y)
=(2x)2-y2
=4x2-y2.
(2)
(3)(-5a+3b)(-5a-3b).
(3)
(-5a+3b)(-5a-3b)
=(-5a)2-(3b)2
=25a2-9b2.
CONTENTS
3
随堂练习
1.计算(2x+3)(2x-3)的值是( )
A.4x2-9 B.4x2-3
C.2x2-9 D.2x2-3
2.已知a=7202,b=719×721,则( )
A.a=b B.a>b
C.a<b D.a≤b
A
A
3.已知(-3a+m)(4b+n)=16b2-9a2,则m,n的值分别为( )
A.m=-4b,n=3a
B.m=4b,n=-3a
C.m=4b,n=3a
D.m=3a,n=4b
4.计算:
(1)(x+1)(x-____)=x2-1;
(2)(x+3y)______=9y2-x2.
C
(3y-x)
1
5.运用平方差公式计算:
(1)(m+1)(m-1)(m2+1); (2)503×497;
(3) (x-y)(x+y)(x2+y2)(x4+y4).
解:(m+1)(m-1)(m2+1)
=(m2-1)(m2+1).
=m4-1
=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
解:(x-y)(x+y)(x2+y2)(x4+y4)
=249991
解:503×497
=(500+3)(500-3)
=5002-32
6.某公园原有长方形绿地一块,现进行如下改造,将长减少2 m,将宽增加2 m,改造后得到一块正方形绿地,它的面积是原绿地面积的2倍,求改造后正方形绿地的面积.
解:设改造后正方形绿地的边长为x m,
则改造前的长是(x+2) m,宽是(x-2) m.
根据题意,有2(x+2)(x-2)=x2,
即2(x2-4)=x2,
可得x2=8.
答:改造后正方形绿地的面积为8 m2.
CONTENTS
4
课堂小结
平方差公式
内容
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
运用
只有符合公式条件的乘法,才能运用公式简化运算,其余运算仍按乘法法则进行
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
