9.3 三角形的角平分线、中线和高 优质课件(35张PPT)
文档属性
| 名称 | 9.3 三角形的角平分线、中线和高 优质课件(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览








文档简介
第九章 三角形
9.3 三角形的角平分线、中线和高
1
2
3
CONTENTS
1
想一想:
这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?
CONTENTS
2
三角形的角平分线
A
C
B
O
∠AOC= ∠BOC
问题1.1
如图,若OC是∠AOB的平分线,你能得到什么结论?
三角形的角平分线
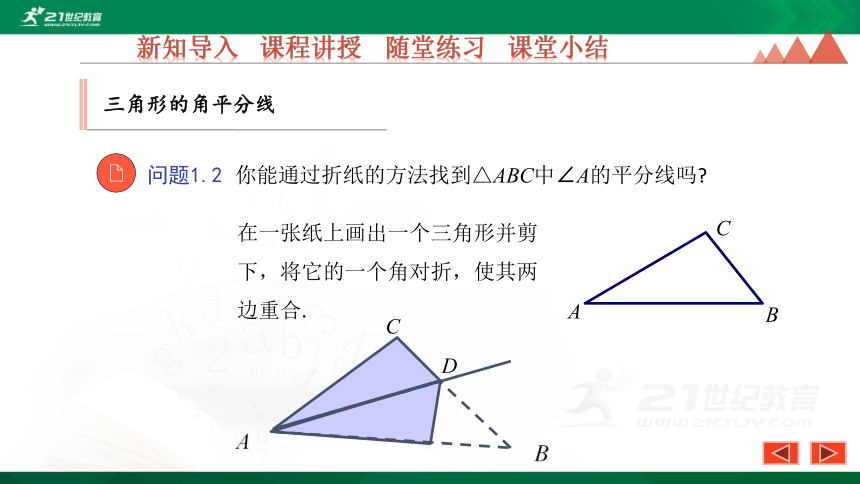
问题1.2
你能通过折纸的方法找到△ABC中∠A的平分线吗?
C
A
B
在一张纸上画出一个三角形并剪下,将它的一个角对折,使其两边重合.
A
C
B
D
三角形的角平分线
定义:三角形一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段叫作三角形的角平分线.
提示:角平分线是一条射线,
三角形的角平分线是一条线段.
三角形的角平分线
1
2
A
B
C
D
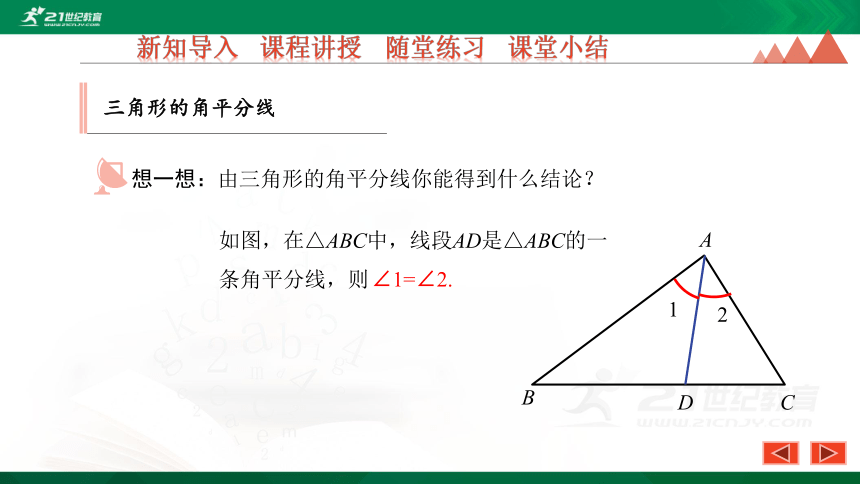
如图,在△ABC中,线段AD是△ABC的一条角平分线,则
∠1=∠2.
想一想:由三角形的角平分线你能得到什么结论?
三角形的角平分线
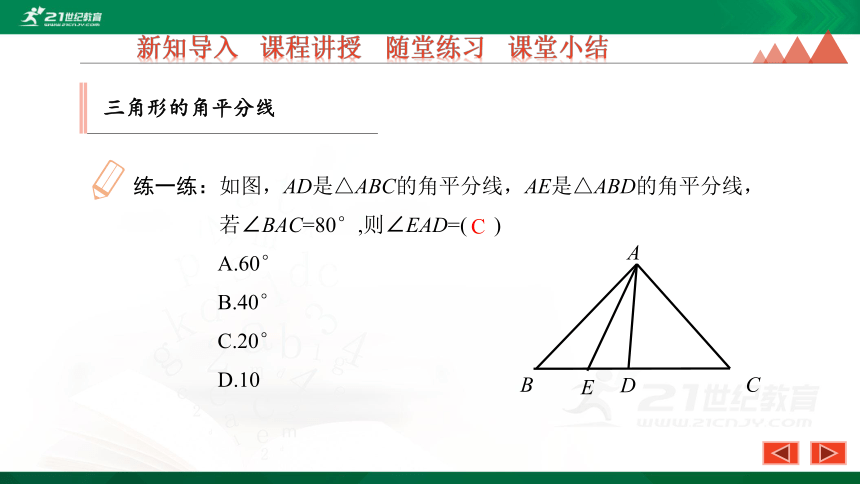
练一练:如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=80°,则∠EAD=( )
A.60°
B.40°
C.20°
D.10
C
C
A
B
D
E
三角形的角平分线
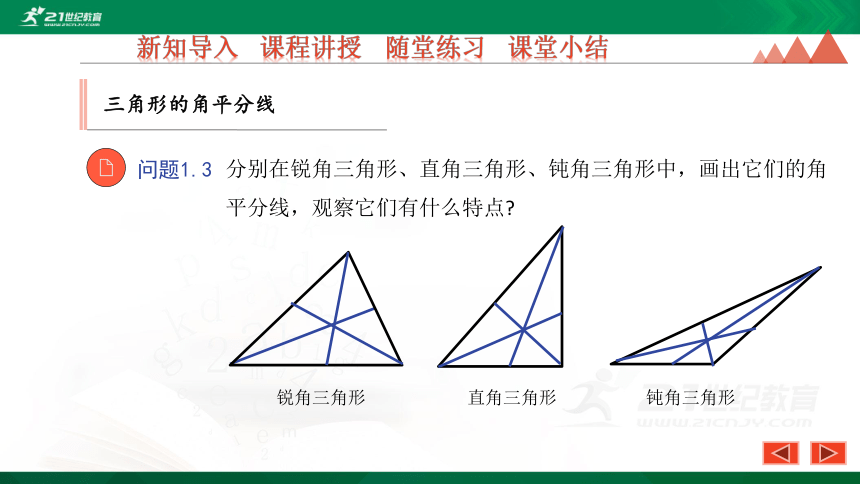
问题1.3
分别在锐角三角形、直角三角形、钝角三角形中,画出它们的角平分线,观察它们有什么特点?
锐角三角形
钝角三角形
直角三角形
三角形的角平分线
归纳:一个三角形有三条角平分线,并且都在三角形内部,三角形的三条角平分线交于同一点.
三角形的中线
问题2.1
如图,如果点C是线段AB的中点,你能得到什么结论?
A
C
B
AC=BC= AB
三角形的中线
问题2.2
类比三角形的角平分线的概念,试说明什么叫三角形的中线?
A
B
C
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
D
定义: 连接三角形的一个顶点与它对边中线的线段叫作三角形的中线.
三角形的中线
如图,在△ABC中,线段AD是△ABC的边BC上的中线,则BD=DC
A
B
C
D
想一想:由三角形的中线你能得到什么结论?
三角形的中线
练一练:如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35 cm,BC=11 cm,且△ABD与△ACD的周长之差为3 cm,求AB与AC的长.
A
C
D
B
三角形的中线
解:∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
又∵△ABD与△ACD的周长之差为3cm,
∴AB-AC=3,
∴AB=13.5cm,AC=10.5cm.
A
C
D
B
三角形的中线
问题2.3
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
三角形的中线
归纳:三角形有三条中线,这三条中线相交于一点,这个交点叫作这个三角形的重心.
三角形的高
问题3.1
根据我们已经学过知识,试着说出三角形高的定义.
定义: 三角形的一个顶点到它对边所在直线的垂线段叫作三角形的高线,简称三角形的高.
A
B
C
D
垂直符号
垂足
三角形的高
如图,在△ABC中,线段AD是△ABC的边BC上的高,则∠ADB= ∠ADC=90 °
想一想:由三角形的高你能得到什么结论?
A
B
C
D
三角形的高
问题3.2
分别在锐角三角形、直角三角形、钝角三角形中,画出它们的高,观察它们有什么特点?
三角形的高
归纳:三角形有三条高,这三条高相交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
三角形的高
练一练:若三角形某条边上的高的位置在该三角形内,则该边所对的角一定是( )
A.锐角 B.直角
C.钝角 D.以上都有可能
D
三角形的高
试一试:回顾本堂课学习的知识,完成下面的表格.
三角形的
重要线段
概念
图示
表述方式
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,_____和_____之间的_____
三角形
的中线
三角形中,连结一个顶点和它对边____的____
三角形的
角平分线
三角形一个内角的________与它的对边相交,这个角顶点与交点之间的____
顶点
垂足
线段
中点
线段
平分线
线段
A
B
D
C
A
B
D
C
∵ AD是△ABC的中线.
∴ BD=CD= ?BC.
∵AD是△ABC的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
∵.AD是∠BAC的平分线
∴ ∠1=∠2= ? ∠BAC
A
B
D
C
1
2
CONTENTS
3
1.如图,若AD是△ABC的中线,有下列结论:①BD=CD;②AB=AC;③S△ABD=1/2S△ABC.其中一定成立的结论有( )
A.3个
B.2个
C.1个
D.0个
A
B
D
C
B
2.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
3.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
4. 如果一个三角形的三条高的交点恰是三角形的一个顶点,
那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
B
5.如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,
∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
CONTENTS
4
三角形中几条重要线段
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
中线
角平分线
高
三角形的角平分线是一条线段
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
9.3 三角形的角平分线、中线和高
1
2
3
CONTENTS
1
想一想:
这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?
CONTENTS
2
三角形的角平分线
A
C
B
O
∠AOC= ∠BOC
问题1.1
如图,若OC是∠AOB的平分线,你能得到什么结论?
三角形的角平分线
问题1.2
你能通过折纸的方法找到△ABC中∠A的平分线吗?
C
A
B
在一张纸上画出一个三角形并剪下,将它的一个角对折,使其两边重合.
A
C
B
D
三角形的角平分线
定义:三角形一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段叫作三角形的角平分线.
提示:角平分线是一条射线,
三角形的角平分线是一条线段.
三角形的角平分线
1
2
A
B
C
D
如图,在△ABC中,线段AD是△ABC的一条角平分线,则
∠1=∠2.
想一想:由三角形的角平分线你能得到什么结论?
三角形的角平分线
练一练:如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=80°,则∠EAD=( )
A.60°
B.40°
C.20°
D.10
C
C
A
B
D
E
三角形的角平分线
问题1.3
分别在锐角三角形、直角三角形、钝角三角形中,画出它们的角平分线,观察它们有什么特点?
锐角三角形
钝角三角形
直角三角形
三角形的角平分线
归纳:一个三角形有三条角平分线,并且都在三角形内部,三角形的三条角平分线交于同一点.
三角形的中线
问题2.1
如图,如果点C是线段AB的中点,你能得到什么结论?
A
C
B
AC=BC= AB
三角形的中线
问题2.2
类比三角形的角平分线的概念,试说明什么叫三角形的中线?
A
B
C
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
D
定义: 连接三角形的一个顶点与它对边中线的线段叫作三角形的中线.
三角形的中线
如图,在△ABC中,线段AD是△ABC的边BC上的中线,则BD=DC
A
B
C
D
想一想:由三角形的中线你能得到什么结论?
三角形的中线
练一练:如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35 cm,BC=11 cm,且△ABD与△ACD的周长之差为3 cm,求AB与AC的长.
A
C
D
B
三角形的中线
解:∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
又∵△ABD与△ACD的周长之差为3cm,
∴AB-AC=3,
∴AB=13.5cm,AC=10.5cm.
A
C
D
B
三角形的中线
问题2.3
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
三角形的中线
归纳:三角形有三条中线,这三条中线相交于一点,这个交点叫作这个三角形的重心.
三角形的高
问题3.1
根据我们已经学过知识,试着说出三角形高的定义.
定义: 三角形的一个顶点到它对边所在直线的垂线段叫作三角形的高线,简称三角形的高.
A
B
C
D
垂直符号
垂足
三角形的高
如图,在△ABC中,线段AD是△ABC的边BC上的高,则∠ADB= ∠ADC=90 °
想一想:由三角形的高你能得到什么结论?
A
B
C
D
三角形的高
问题3.2
分别在锐角三角形、直角三角形、钝角三角形中,画出它们的高,观察它们有什么特点?
三角形的高
归纳:三角形有三条高,这三条高相交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
三角形的高
练一练:若三角形某条边上的高的位置在该三角形内,则该边所对的角一定是( )
A.锐角 B.直角
C.钝角 D.以上都有可能
D
三角形的高
试一试:回顾本堂课学习的知识,完成下面的表格.
三角形的
重要线段
概念
图示
表述方式
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,_____和_____之间的_____
三角形
的中线
三角形中,连结一个顶点和它对边____的____
三角形的
角平分线
三角形一个内角的________与它的对边相交,这个角顶点与交点之间的____
顶点
垂足
线段
中点
线段
平分线
线段
A
B
D
C
A
B
D
C
∵ AD是△ABC的中线.
∴ BD=CD= ?BC.
∵AD是△ABC的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
∵.AD是∠BAC的平分线
∴ ∠1=∠2= ? ∠BAC
A
B
D
C
1
2
CONTENTS
3
1.如图,若AD是△ABC的中线,有下列结论:①BD=CD;②AB=AC;③S△ABD=1/2S△ABC.其中一定成立的结论有( )
A.3个
B.2个
C.1个
D.0个
A
B
D
C
B
2.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
3.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
4. 如果一个三角形的三条高的交点恰是三角形的一个顶点,
那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
B
5.如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,
∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
CONTENTS
4
三角形中几条重要线段
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
中线
角平分线
高
三角形的角平分线是一条线段
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
