10.5 第2课时 解较复杂的一元一次不等式组 优质课件(24张PPT)
文档属性
| 名称 | 10.5 第2课时 解较复杂的一元一次不等式组 优质课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 00:00:00 | ||
图片预览







文档简介
第十章 一元一次不等式和
一元一次不等式组
10.5 一元一次不等式组
第2课时 解较复杂的一元一次不等式组
1
CONTENTS
1
想一想:
在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形?
所以,x的取值范围为4利用三角形三边关系可知:
CONTENTS
2
解较复杂的一元一次不等式组
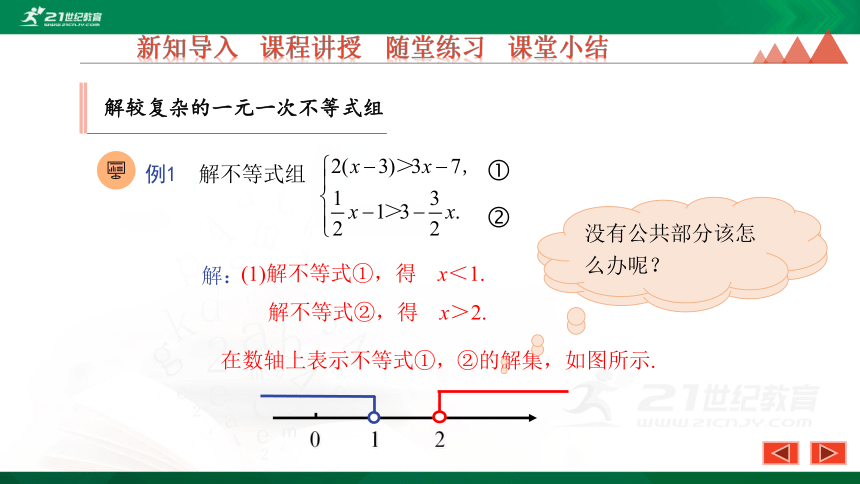
例1 解不等式组
?
?
解:
(1)解不等式①,得 x<1.
解不等式②,得 x>2.
在数轴上表示不等式①,②的解集,如图所示.
0 1 2
这两个不等式的解集有公共部分吗?
没有公共部分该怎么办呢?
解较复杂的一元一次不等式组
归纳:两个不等式的解集可能会出现无公共部分的情况,此时,称这个不等式组无解.
解较复杂的一元一次不等式组
练一练:解下列不等式组:
?
?
?
?
解较复杂的一元一次不等式组
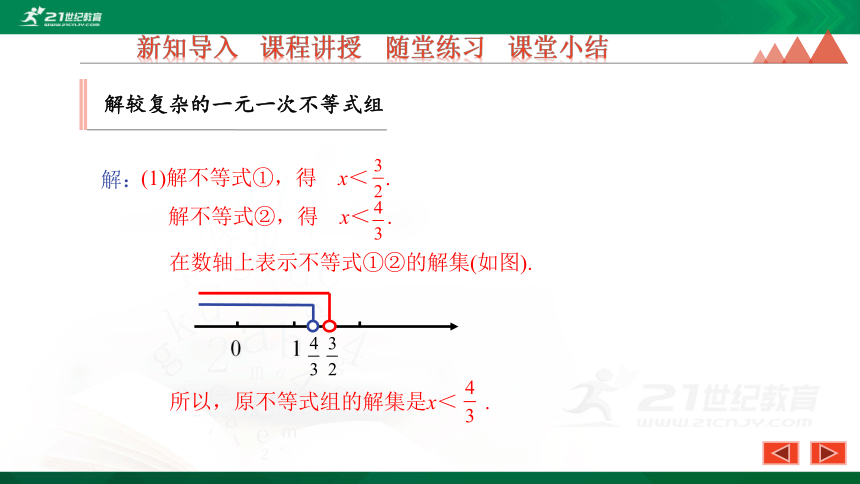
解:
(1)解不等式①,得 x< .
解不等式②,得 x< .
在数轴上表示不等式①②的解集(如图).
所以,原不等式组的解集是x< .
0 1
解较复杂的一元一次不等式组
(2)解不等式①,得 x>
解不等式②,得 x≥4.
在数轴上表示不等式①②的解集(如图).
0 4
所以,原不等式组的解集是x≥4.
解较复杂的一元一次不等式组
想一想:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
解较复杂的一元一次不等式组
归纳:解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
解较复杂的一元一次不等式组
例2 求不等式组 的整数解.
?
?
解:
解不等式①,得x> .
解不等式②,得x< .
所以,不等式组的解集是 <x< .
因此,不等式组的整数解是0,1,2.
CONTENTS
3
1.不等式组 的最大整数解为( )
A.8 B.6
C.5 D.4
C
2.若关于x的一元一次不等式组
的解集是x<5,则m的取值范围是( )
A.m≥5 B.m>5
C.m≤5 D.m<5
A
3.解下列不等式组:
解:(1) 1<x<5;
(2)-4<x≤1;
4.x取哪些正整数值时,不等式x+3>6与2x-1<10都成立?
解:
解不等式组
得3所以x可取的正整数值是4,5.
5.某中学学生会在学期末购买了一批纪念品发给会员.如果分给每位会员4个,那么剩下28个纪念品;如果分给每位会员5个纪念品,那么最后一位会员分得的纪念品不足4个,但至少有1个,求该中学学生会最少有多少个会员.
解:设该中学学生会有x个会员,则共购买了(4x+28)个纪念品.
根据题意,得 5(x-1)+4>4x+28,
5(x-1)+1≤4x+28.
解得 29∴x的最小值为30.
答:该中学学生会最少有30个会员.
CONTENTS
4
一元一次不等式组
实际应用
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
解较复杂的一元一次不等式组
→
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
一元一次不等式组
10.5 一元一次不等式组
第2课时 解较复杂的一元一次不等式组
1
CONTENTS
1
想一想:
在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形?
所以,x的取值范围为4
CONTENTS
2
解较复杂的一元一次不等式组
例1 解不等式组
?
?
解:
(1)解不等式①,得 x<1.
解不等式②,得 x>2.
在数轴上表示不等式①,②的解集,如图所示.
0 1 2
这两个不等式的解集有公共部分吗?
没有公共部分该怎么办呢?
解较复杂的一元一次不等式组
归纳:两个不等式的解集可能会出现无公共部分的情况,此时,称这个不等式组无解.
解较复杂的一元一次不等式组
练一练:解下列不等式组:
?
?
?
?
解较复杂的一元一次不等式组
解:
(1)解不等式①,得 x< .
解不等式②,得 x< .
在数轴上表示不等式①②的解集(如图).
所以,原不等式组的解集是x< .
0 1
解较复杂的一元一次不等式组
(2)解不等式①,得 x>
解不等式②,得 x≥4.
在数轴上表示不等式①②的解集(如图).
0 4
所以,原不等式组的解集是x≥4.
解较复杂的一元一次不等式组
想一想:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa
解较复杂的一元一次不等式组
归纳:解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
解较复杂的一元一次不等式组
例2 求不等式组 的整数解.
?
?
解:
解不等式①,得x> .
解不等式②,得x< .
所以,不等式组的解集是 <x< .
因此,不等式组的整数解是0,1,2.
CONTENTS
3
1.不等式组 的最大整数解为( )
A.8 B.6
C.5 D.4
C
2.若关于x的一元一次不等式组
的解集是x<5,则m的取值范围是( )
A.m≥5 B.m>5
C.m≤5 D.m<5
A
3.解下列不等式组:
解:(1) 1<x<5;
(2)-4<x≤1;
4.x取哪些正整数值时,不等式x+3>6与2x-1<10都成立?
解:
解不等式组
得3
5.某中学学生会在学期末购买了一批纪念品发给会员.如果分给每位会员4个,那么剩下28个纪念品;如果分给每位会员5个纪念品,那么最后一位会员分得的纪念品不足4个,但至少有1个,求该中学学生会最少有多少个会员.
解:设该中学学生会有x个会员,则共购买了(4x+28)个纪念品.
根据题意,得 5(x-1)+4>4x+28,
5(x-1)+1≤4x+28.
解得 29
答:该中学学生会最少有30个会员.
CONTENTS
4
一元一次不等式组
实际应用
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
解较复杂的一元一次不等式组
→
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
