11.1 因式分解 优质课件(22张PPT)
文档属性
| 名称 | 11.1 因式分解 优质课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览








文档简介
第十一章 因式分解
11.1 因式分解
1
CONTENTS
1
想一想:
观察下面几个多项式的乘法算式:
ma+mb=m(a+b)
a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
多项式乘法是把几个整式的乘积化为一个多项式.反过来,你能将一个多项式分解成几个整式乘积的形式吗?
CONTENTS
2
因式分解的概念
问题1
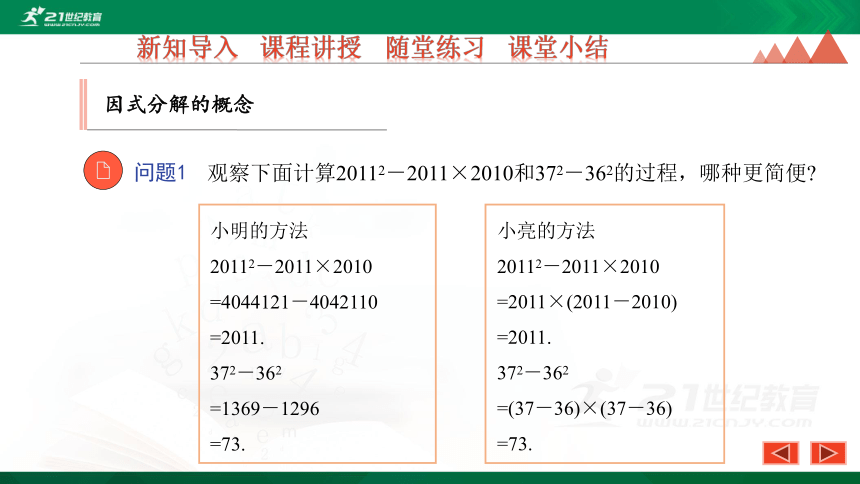
观察下面计算20112-2011×2010和372-362的过程,哪种更简便?
小明的方法
20112-2011×2010
=4044121-4042110
=2011.
372-362
=1369-1296
=73.
小亮的方法
20112-2011×2010
=2011×(2011-2010)
=2011.
372-362
=(37-36)×(37-36)
=73.
因式分解的概念
(1)小明用的什么方法?
(2)小亮的第一个算式用了什么方法?
(3)小亮的第二个算式用了什么方法?
根据乘方的意义直接进行计算.
乘法对加法的分配律的逆用.
平方差公式.
因式分解的概念
问题2
(1)观察下面三个算式:
x(x-2)=x2-2x,(x+y)(x-y)=x2-y2,(x+1)2=x2+2x+1.
(2)上面三个算式能反过来,写成整式乘积的形式吗?
可以.x2-2x=x(x-2),
x2-y2=(x+y)(x-y),
x2+2x+1=(x+1)2.
因式分解的概念
定义:像这样,把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解,也叫做将多项式分解因式,其中每个整式都叫做这个多项式的因式.
因式分解的概念
问题3
计算下列式子.
(1)m(a+b-1)= ;?
(2)(m+4)(m-4)= ;?
(3)(y-3)2= ;?
根据上面的算式填空.
(1)ma+mb-m= ;?
(2)m2-16= ;?
(3)y2-6y+9= .?
因式分解与整式的乘法有什么关系?
ma+mb-m
m2-16
y2-6y+9
m(a+b-1)
(m+4)(m-4)
(y-3)2
因式分解的概念
归纳:多项式的因式分解与乘法运算是不同的.多项式的因式分解是把一个多项式化成几个整式的乘积,而多项式的乘法运算是把几个整式的乘积化成一个多项式.可见,多项式的因式分解与多项式的乘法运算是相反的变形过程,如图所示.
因式分解的概念
试一试:1.下列各式中,从等号左边到右边的变形,哪些是多项式的因式分解?
(1)x2-4=(x+2)(x-2);
(2)x2+4x+4=(x+2)2;
(3)7m+14n=7(m+2n);
(4)x(y+1)=xy+x.
(1)(2)(3)是,(4)不是.
因式分解的概念
2.下列对多项式的变形,哪些是因式分解?是因式分解的,指出它的各因式.
(1)x2-x=x(x-1);
(2)10x+5y=5(2x+y);
(3)a2-1=(a+1)(a-1);
(4)x2-2x+1=(x-1)2.
试一试:
(1)是,因式为x,x-1;
(2)是,因式为5,2x+y;
(3)是,因式为a+1,a-1;
(4)是,因式为x-1,x-1.
CONTENTS
3
1. 下列各式中从左到右的变形属于分解因式的是( )
A. a(a+b-1)=a2+ab-a
B. a2-a-2=a(a-1)-2
C. -4a2+9b2=(-2a+3b)(2a+3b)
D.2x +1=x(2+ )
C
2.把x2+3x+c分解因式得x2+3x+c=(x+1)·(x+2),则c的值为( )
A.2 B.3
C.-2 D.-3
A
3.若42x2-31x+2能分解成两个因式的乘积且有一个因式为6x-4,设另一个因式为mx-n,其中m,n为常数,请你求出m,n的值.
解:(6x-4)(mx-n)=6mx2-4mx-6nx+4n=6mx2-(4m+6n)x+4n,
由题意可得42x2-31x+2=6mx2-(4m+6n)x+4n,
4. 把多项式x2+4mx+5因式分解得(x+5)(x+n),求m+n的值.
解:由题意,得
x2+4mx+5=(x+5)(x+n)
=x2+(n+5)x+5n,
5n=5,4m=n+5.
解得n=1,m= ,
m+n=1+ = .
CONTENTS
4
因式分解
把一个多项式化为几个整式的乘积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.其中,每个整式叫做这个多项式的因式
定义
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
11.1 因式分解
1
CONTENTS
1
想一想:
观察下面几个多项式的乘法算式:
ma+mb=m(a+b)
a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
多项式乘法是把几个整式的乘积化为一个多项式.反过来,你能将一个多项式分解成几个整式乘积的形式吗?
CONTENTS
2
因式分解的概念
问题1
观察下面计算20112-2011×2010和372-362的过程,哪种更简便?
小明的方法
20112-2011×2010
=4044121-4042110
=2011.
372-362
=1369-1296
=73.
小亮的方法
20112-2011×2010
=2011×(2011-2010)
=2011.
372-362
=(37-36)×(37-36)
=73.
因式分解的概念
(1)小明用的什么方法?
(2)小亮的第一个算式用了什么方法?
(3)小亮的第二个算式用了什么方法?
根据乘方的意义直接进行计算.
乘法对加法的分配律的逆用.
平方差公式.
因式分解的概念
问题2
(1)观察下面三个算式:
x(x-2)=x2-2x,(x+y)(x-y)=x2-y2,(x+1)2=x2+2x+1.
(2)上面三个算式能反过来,写成整式乘积的形式吗?
可以.x2-2x=x(x-2),
x2-y2=(x+y)(x-y),
x2+2x+1=(x+1)2.
因式分解的概念
定义:像这样,把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解,也叫做将多项式分解因式,其中每个整式都叫做这个多项式的因式.
因式分解的概念
问题3
计算下列式子.
(1)m(a+b-1)= ;?
(2)(m+4)(m-4)= ;?
(3)(y-3)2= ;?
根据上面的算式填空.
(1)ma+mb-m= ;?
(2)m2-16= ;?
(3)y2-6y+9= .?
因式分解与整式的乘法有什么关系?
ma+mb-m
m2-16
y2-6y+9
m(a+b-1)
(m+4)(m-4)
(y-3)2
因式分解的概念
归纳:多项式的因式分解与乘法运算是不同的.多项式的因式分解是把一个多项式化成几个整式的乘积,而多项式的乘法运算是把几个整式的乘积化成一个多项式.可见,多项式的因式分解与多项式的乘法运算是相反的变形过程,如图所示.
因式分解的概念
试一试:1.下列各式中,从等号左边到右边的变形,哪些是多项式的因式分解?
(1)x2-4=(x+2)(x-2);
(2)x2+4x+4=(x+2)2;
(3)7m+14n=7(m+2n);
(4)x(y+1)=xy+x.
(1)(2)(3)是,(4)不是.
因式分解的概念
2.下列对多项式的变形,哪些是因式分解?是因式分解的,指出它的各因式.
(1)x2-x=x(x-1);
(2)10x+5y=5(2x+y);
(3)a2-1=(a+1)(a-1);
(4)x2-2x+1=(x-1)2.
试一试:
(1)是,因式为x,x-1;
(2)是,因式为5,2x+y;
(3)是,因式为a+1,a-1;
(4)是,因式为x-1,x-1.
CONTENTS
3
1. 下列各式中从左到右的变形属于分解因式的是( )
A. a(a+b-1)=a2+ab-a
B. a2-a-2=a(a-1)-2
C. -4a2+9b2=(-2a+3b)(2a+3b)
D.2x +1=x(2+ )
C
2.把x2+3x+c分解因式得x2+3x+c=(x+1)·(x+2),则c的值为( )
A.2 B.3
C.-2 D.-3
A
3.若42x2-31x+2能分解成两个因式的乘积且有一个因式为6x-4,设另一个因式为mx-n,其中m,n为常数,请你求出m,n的值.
解:(6x-4)(mx-n)=6mx2-4mx-6nx+4n=6mx2-(4m+6n)x+4n,
由题意可得42x2-31x+2=6mx2-(4m+6n)x+4n,
4. 把多项式x2+4mx+5因式分解得(x+5)(x+n),求m+n的值.
解:由题意,得
x2+4mx+5=(x+5)(x+n)
=x2+(n+5)x+5n,
5n=5,4m=n+5.
解得n=1,m= ,
m+n=1+ = .
CONTENTS
4
因式分解
把一个多项式化为几个整式的乘积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.其中,每个整式叫做这个多项式的因式
定义
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
