20.4 函数的初步应用 优质课件(22张PPT)
文档属性
| 名称 | 20.4 函数的初步应用 优质课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 12:00:32 | ||
图片预览








文档简介
第二十章 函 数
20.4 函数的初步应用
1
CONTENTS
1
看一看:
很多实际问题和数学问题都表现为两个变量之间的函数关系.因此,学会建立函数模型,并用函数模型解决问题,是十分重要的.
CONTENTS
2
函数的初步应用
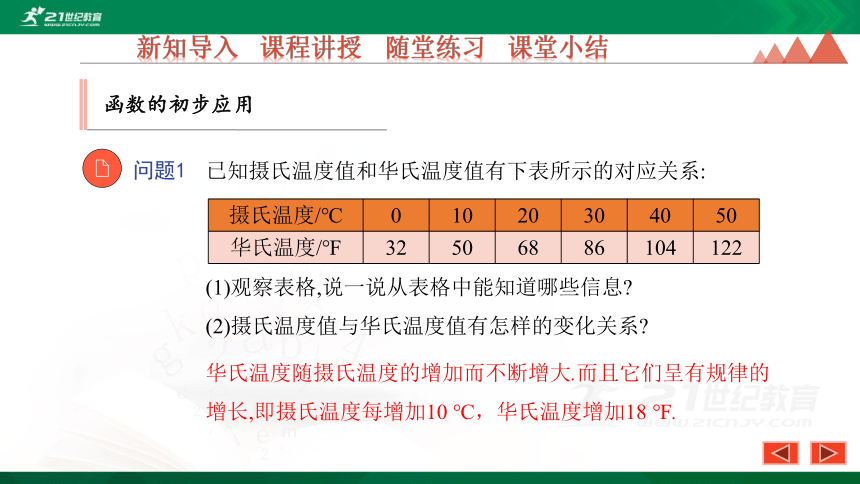
问题1
已知摄氏温度值和华氏温度值有下表所示的对应关系:
(1)观察表格,说一说从表格中能知道哪些信息?
(2)摄氏温度值与华氏温度值有怎样的变化关系?
摄氏温度/℃
0
10
20
30
40
50
华氏温度/℉
32
50
68
86
104
122
华氏温度随摄氏温度的增加而不断增大.而且它们呈有规律的增长,即摄氏温度每增加10 ℃,华氏温度增加18 ℉.
函数的初步应用
(3)当摄氏温度为30 ℃时,由数值表能直接求出华氏温度吗?
(4)如果设摄氏温度为x ℃,华氏温度为y ℉,你能表示出x和y之间的函数关系吗?
y=1.8x+32.
能,为86 ℉.
函数的初步应用
问题2
五环图的示意图如图所示,上面三个环中的数字是三个连续的偶数,下面两个环中的数字是两个连续的奇数,并且三个偶数之和与两个奇数之和相等.请你再写出几组具有这种关系的五个数.
函数的初步应用
通过列举发现满足条件的数字有无数组,那么它们之间是否也存在着一定的函数关系呢?
用2x-2,2x,2x+2表示三个连续的偶数,用2y-1和2y+1表示两个连续的奇数,求y与x之间满足的关系式.
y= x.
函数的初步应用
归纳:函数表达式具有简单明确、易于深入研究的特点,能准确地反映整个变化过程中自变量与函数的对应关系.因此,有些实际问题若能求出函数表达式,就可以利用函数表达式分析和判断变化的过程和结果.
函数的初步应用
做一做:1.一支20 cm长的蜡烛,点燃后,每小时燃烧5 cm.在图中,哪幅图像能大致刻画出这支蜡烛点燃后剩下的长度h(cm)与点燃时间t(h)之间的函数关系?请说明理由.
图(3),理由略.
函数的初步应用
2.一等腰三角形的周长为12 cm,设其底边长为y cm,腰长为x cm.
(1)写出y与x的函数关系式,并指出自变量x的取值范围.
(2)画出这个函数的图像.
(1)y=12-2x,3(2)略.
CONTENTS
3
1.豪豪和欢欢相约星期六下午一起去电影院看电影,欢欢走到半路时发现电影票没带,于是以相同的速度折返回去,回家找了一会,拿上电影票快步跑向电影院,则欢欢离电影院的距离y与时间t之间的函数关系的大致图像是图中的( )
B
2.为了节能减排,鼓励居民节约用电,某市将出台新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.50元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按每度电0.50元计算).现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图像表示正确的是( )
C
3.某市一周平均气温(℃)如图所示,下列说法不正确的是( )
A.星期二的平均气温最高
B.星期四到星期日天气逐渐转暖
C.这一周最高气温与最低气温相差4 ℃
D.星期四的平均气温最低
C
4.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
解:(1)依题意得:学校离王老师家有10千米;从出发到学校,王老师用了25分钟.
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后
的速度快?最快时速达到多少?
(2)依题意得王老师吃早餐用了10分钟.
(3)吃早餐以前的速度为5÷10=0.5(千米/分),吃完早餐以后的速度为(10-5)÷(25-20)=1(千米/分),即60 千米/时,
∴王老师吃完早餐以后的速度快,最快时速达到60千米/时.
CONTENTS
4
函数的初步应用
函数表达式的应用
函数图像的应用
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
20.4 函数的初步应用
1
CONTENTS
1
看一看:
很多实际问题和数学问题都表现为两个变量之间的函数关系.因此,学会建立函数模型,并用函数模型解决问题,是十分重要的.
CONTENTS
2
函数的初步应用
问题1
已知摄氏温度值和华氏温度值有下表所示的对应关系:
(1)观察表格,说一说从表格中能知道哪些信息?
(2)摄氏温度值与华氏温度值有怎样的变化关系?
摄氏温度/℃
0
10
20
30
40
50
华氏温度/℉
32
50
68
86
104
122
华氏温度随摄氏温度的增加而不断增大.而且它们呈有规律的增长,即摄氏温度每增加10 ℃,华氏温度增加18 ℉.
函数的初步应用
(3)当摄氏温度为30 ℃时,由数值表能直接求出华氏温度吗?
(4)如果设摄氏温度为x ℃,华氏温度为y ℉,你能表示出x和y之间的函数关系吗?
y=1.8x+32.
能,为86 ℉.
函数的初步应用
问题2
五环图的示意图如图所示,上面三个环中的数字是三个连续的偶数,下面两个环中的数字是两个连续的奇数,并且三个偶数之和与两个奇数之和相等.请你再写出几组具有这种关系的五个数.
函数的初步应用
通过列举发现满足条件的数字有无数组,那么它们之间是否也存在着一定的函数关系呢?
用2x-2,2x,2x+2表示三个连续的偶数,用2y-1和2y+1表示两个连续的奇数,求y与x之间满足的关系式.
y= x.
函数的初步应用
归纳:函数表达式具有简单明确、易于深入研究的特点,能准确地反映整个变化过程中自变量与函数的对应关系.因此,有些实际问题若能求出函数表达式,就可以利用函数表达式分析和判断变化的过程和结果.
函数的初步应用
做一做:1.一支20 cm长的蜡烛,点燃后,每小时燃烧5 cm.在图中,哪幅图像能大致刻画出这支蜡烛点燃后剩下的长度h(cm)与点燃时间t(h)之间的函数关系?请说明理由.
图(3),理由略.
函数的初步应用
2.一等腰三角形的周长为12 cm,设其底边长为y cm,腰长为x cm.
(1)写出y与x的函数关系式,并指出自变量x的取值范围.
(2)画出这个函数的图像.
(1)y=12-2x,3
CONTENTS
3
1.豪豪和欢欢相约星期六下午一起去电影院看电影,欢欢走到半路时发现电影票没带,于是以相同的速度折返回去,回家找了一会,拿上电影票快步跑向电影院,则欢欢离电影院的距离y与时间t之间的函数关系的大致图像是图中的( )
B
2.为了节能减排,鼓励居民节约用电,某市将出台新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.50元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按每度电0.50元计算).现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图像表示正确的是( )
C
3.某市一周平均气温(℃)如图所示,下列说法不正确的是( )
A.星期二的平均气温最高
B.星期四到星期日天气逐渐转暖
C.这一周最高气温与最低气温相差4 ℃
D.星期四的平均气温最低
C
4.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
解:(1)依题意得:学校离王老师家有10千米;从出发到学校,王老师用了25分钟.
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后
的速度快?最快时速达到多少?
(2)依题意得王老师吃早餐用了10分钟.
(3)吃早餐以前的速度为5÷10=0.5(千米/分),吃完早餐以后的速度为(10-5)÷(25-20)=1(千米/分),即60 千米/时,
∴王老师吃完早餐以后的速度快,最快时速达到60千米/时.
CONTENTS
4
函数的初步应用
函数表达式的应用
函数图像的应用
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
