21.4 第2课时 一次函数的应用(2) 优质课件(29张PPT)
文档属性
| 名称 | 21.4 第2课时 一次函数的应用(2) 优质课件(29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 14:11:40 | ||
图片预览








文档简介
第二十一章 一次函数
21.4 一次函数的应用
第2课时 一次函数的应用(2)
1
CONTENTS
1
想一想:
我该如何选择方案呢?
每月交15元月租费通话1分钟付话费0.3元
甲种业务
不要月租费每通话1分钟付话费0.6元
乙种业务
CONTENTS
2
例 甲骑自行车以10 km/h的速度沿公路行驶,出发3 h后,乙骑摩托车从同一地点出发沿公路与甲同向行驶,速度为25 km/h.
(1)设甲离开出发地的时间为x(h),求:
①甲离开出发地的路程y(km)与x(h)之间的函数关系式,并指出自变量x的取值范围.
三个“一次”的关系
解:(1)由公式s=vt,得
①甲离开出发地的路程y与x的函数关系式为y=10x.自变量x的取值范围为x≥0.
三个“一次”的关系
②乙离开出发地的路程y(km)与x(h)之间的函数关系式,并指出自变量x的取值范围.
②乙离开出发地的路程y与x的函数关系式为y=25(x-3),即y=25x-75.自变量x的取值范围为x≥3.
三个“一次”的关系
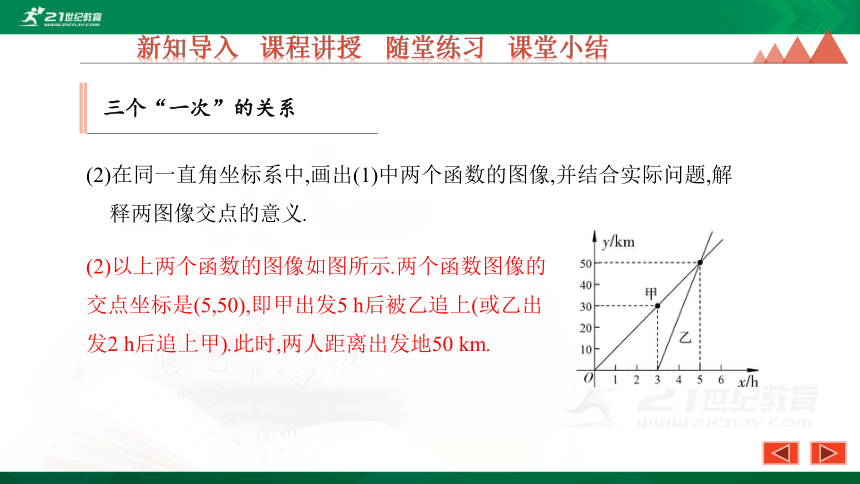
(2)在同一直角坐标系中,画出(1)中两个函数的图像,并结合实际问题,解释两图像交点的意义.
(2)以上两个函数的图像如图所示.两个函数图像的交点坐标是(5,50),即甲出发5 h后被乙追上(或乙出发2 h后追上甲).此时,两人距离出发地50 km.
三个“一次”的关系
想一想:对于上例中甲、乙行驶的情况,你能借助图解释“乙出发多少小时后可以超过甲”这一问题吗?还有其他方法解答这个问题吗?
当x>5时,y=25(x-3)的图像在y=10x的图像的上方,说明乙出发2小时后,乙可以超过甲,还可以用25x>10(x+3)来解决这个问题,其中x表示乙离开出发地的时间.
三个“一次”的关系
归纳:有些一元一次方程和一元一次不等式问题,可以借助一次函数来考虑,借助一次函数的图像,往往能使方程和不等式的意义更加直观和形象.
三个“一次”的关系
问题1
某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋,现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.
(1)设租用时间为x个月,承租房屋所付租金为y元,分别求租用甲、乙两家的租金y与租用时间x之间的函数关系式.
(2)根据求出的两个函数表达式,试判断租用哪家的房屋更合算.
三个“一次”的关系
解法1:
①要使y甲=y乙,就是要使3000x=2000x+40000,解得x=40,即当x=40时,租哪家租金都相同.
②要使y甲>y乙,就是要使3000x>2000x+40000,解得x>40,即当x>40时,租乙家的房屋更合算.
③要使y甲三个“一次”的关系
解法2:
将两函数的图像在同一坐标系中画出,观察图像可知:
这两个函数图像的交点是(40,120000),也就是当x=40
时,y甲和y乙的值相等,都等于120000;当x>40时,y甲=
3000x的图像在y乙=2000x+40000的图像的上方,这说
明此时y甲>y乙;当x<40时,y甲=3000x的图像在y乙=2000x
+40000的图像的下方,这说明此时y甲三个“一次”的关系
归纳:一元一次方程、一元一次不等式与一次函数的关系:
1.从“数”看一次函数y1=k1x+b1,y2=k2x+b2
(1)函数值y1=y2时x的值 一元一次方程k1x+b1=k2x+b2的解;
(2)函数值y1>y2时x的值 一元一次不等式k1x+b1>k2x+b2的解集;
(3)函数值y1<y2时x的值 一元一次不等式k1x+b1<k2x+b2的解集;
三个“一次”的关系
2.从“形”看一次函数y1=k1x+b1(直线l1),y2=k2x+b2(直线l2)
(1)直线l1与l2 交点的横坐标 一元一次方程k1x+b1=k2x+b2的解;
(2)直线l1在l2 上方部分的点的横坐标 一元一次不等式k1x+b1>k2x+b2的解集;
(3)直线l1在l2 下方部分的点的横坐标 一元一次不等式k1x+b1<k2x+b2的解集;
CONTENTS
3
1.(沈阳中考)在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示,当甲车出发 h时,两车相距350 km.?
2.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为 米.?
2200
3.某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
解:(1)由题意可得:
银卡消费:y=10x+150,普通票消费:y=20x.
(2)在同一坐标系中,若三种消费方式对应的函数图像如图所示,请求出点A,B,C的坐标;
当10x+150=20x时,解得x=15,则y=300,故B(15,300),
当y=10x+150,x=0时,y=150,故A(0,150),
当y=10x+150=600时,解得x=45,则y=600,故C(45,600).
(3)请根据函数图像,直接写出选择哪种消费方式更合算.
如图所示,由A,B,C的坐标可得:
当0当x=15时,银卡、普通票的总费用相同,均比金卡合算;
当15当x=45时,金卡、银卡的总费用相同,均比普通票合算;当x>45时,金卡消费更划算.
4.联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.
(1)分别表示出y1与x,y2与x的函数关系式;
(2)月通话时间为多长时,A,B两种套餐收费一样?
(3)什么情况下A套餐更省钱?
解:(1)A套餐的收费方式:y1=0.1x+15;B套餐的收费方式:y2=0.15x.
(2)由0.1x+15=0.15x,得x=300,即当月通话时间是300分钟时,A,B两种套餐收费一样.
(3)当月通话时间多于300分钟时,A套餐更省钱.
解:(1)设购买甲种鱼苗x尾,乙种鱼苗y尾,
根据题意可得 解得
即购买甲种鱼苗500尾,乙种鱼苗200尾.
5.我市某养殖场计划购买甲、乙两种鱼苗共700尾,甲种鱼苗每尾3元,乙种鱼苗每尾5元,相关资料表明:甲、乙两种鱼苗的成活率分别为85%和90%.
(1)若购买这两种鱼苗共用去2500元,则甲、乙两种鱼苗各购买多少尾?
(2)若要使这批鱼苗的总成活率不低于88%,则甲种鱼苗至多购买多少尾?
解:设购买甲种鱼苗z尾,乙种鱼苗(700-z)尾,
列不等式得85%z+90%(700-z)≥700×88%,
解得z≤280.即甲种鱼苗至多购买280尾.
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的费用最低?并求出最低费用.
解:设甲种鱼苗购买m尾,购买鱼苗的费用为w元,
则w=3m+5(700-m)=-2m+3500,
∵-2<0,∴w随m的增大而减小,
∵0∴当m=280时,w有最小值,w的最小值=3500-2×280=2940(元),
∴700-m=420.
即当选购甲种鱼苗280尾,乙种鱼苗420尾时,总费用最低,最低费用为2940元.
CONTENTS
4
三个“一次”的关系
从“数”看一次函数y1=k1x+b1,y2=k2x+b2
(1)函数值y1=y2时x的值 一元一次方程k1x+b1=k2x+b2的解;
(2)函数值y1>y2时x的值 一元一次不等式k1x+b1>k2x+b2的解集;
(3)函数值y1<y2时x的值 一元一次不等式k1x+b1<k2x+b2的解集;
从“形”看一次函数y1=k1x+b1(直线l1),y2=k2x+b2(直线l2)
(1)直线l1与l2 交点的横坐标 一元一次方程k1x+b1=k2x+b2的解;
(2)直线l1在l2 上方部分的点的横坐标 一元一次不等式k1x+b1>k2x+b2的解集;
(3)直线l1在l2 下方部分的点的横坐标 一元一次不等式k1x+b1<k2x+b2的解集;
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
21.4 一次函数的应用
第2课时 一次函数的应用(2)
1
CONTENTS
1
想一想:
我该如何选择方案呢?
每月交15元月租费通话1分钟付话费0.3元
甲种业务
不要月租费每通话1分钟付话费0.6元
乙种业务
CONTENTS
2
例 甲骑自行车以10 km/h的速度沿公路行驶,出发3 h后,乙骑摩托车从同一地点出发沿公路与甲同向行驶,速度为25 km/h.
(1)设甲离开出发地的时间为x(h),求:
①甲离开出发地的路程y(km)与x(h)之间的函数关系式,并指出自变量x的取值范围.
三个“一次”的关系
解:(1)由公式s=vt,得
①甲离开出发地的路程y与x的函数关系式为y=10x.自变量x的取值范围为x≥0.
三个“一次”的关系
②乙离开出发地的路程y(km)与x(h)之间的函数关系式,并指出自变量x的取值范围.
②乙离开出发地的路程y与x的函数关系式为y=25(x-3),即y=25x-75.自变量x的取值范围为x≥3.
三个“一次”的关系
(2)在同一直角坐标系中,画出(1)中两个函数的图像,并结合实际问题,解释两图像交点的意义.
(2)以上两个函数的图像如图所示.两个函数图像的交点坐标是(5,50),即甲出发5 h后被乙追上(或乙出发2 h后追上甲).此时,两人距离出发地50 km.
三个“一次”的关系
想一想:对于上例中甲、乙行驶的情况,你能借助图解释“乙出发多少小时后可以超过甲”这一问题吗?还有其他方法解答这个问题吗?
当x>5时,y=25(x-3)的图像在y=10x的图像的上方,说明乙出发2小时后,乙可以超过甲,还可以用25x>10(x+3)来解决这个问题,其中x表示乙离开出发地的时间.
三个“一次”的关系
归纳:有些一元一次方程和一元一次不等式问题,可以借助一次函数来考虑,借助一次函数的图像,往往能使方程和不等式的意义更加直观和形象.
三个“一次”的关系
问题1
某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋,现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.
(1)设租用时间为x个月,承租房屋所付租金为y元,分别求租用甲、乙两家的租金y与租用时间x之间的函数关系式.
(2)根据求出的两个函数表达式,试判断租用哪家的房屋更合算.
三个“一次”的关系
解法1:
①要使y甲=y乙,就是要使3000x=2000x+40000,解得x=40,即当x=40时,租哪家租金都相同.
②要使y甲>y乙,就是要使3000x>2000x+40000,解得x>40,即当x>40时,租乙家的房屋更合算.
③要使y甲
解法2:
将两函数的图像在同一坐标系中画出,观察图像可知:
这两个函数图像的交点是(40,120000),也就是当x=40
时,y甲和y乙的值相等,都等于120000;当x>40时,y甲=
3000x的图像在y乙=2000x+40000的图像的上方,这说
明此时y甲>y乙;当x<40时,y甲=3000x的图像在y乙=2000x
+40000的图像的下方,这说明此时y甲
归纳:一元一次方程、一元一次不等式与一次函数的关系:
1.从“数”看一次函数y1=k1x+b1,y2=k2x+b2
(1)函数值y1=y2时x的值 一元一次方程k1x+b1=k2x+b2的解;
(2)函数值y1>y2时x的值 一元一次不等式k1x+b1>k2x+b2的解集;
(3)函数值y1<y2时x的值 一元一次不等式k1x+b1<k2x+b2的解集;
三个“一次”的关系
2.从“形”看一次函数y1=k1x+b1(直线l1),y2=k2x+b2(直线l2)
(1)直线l1与l2 交点的横坐标 一元一次方程k1x+b1=k2x+b2的解;
(2)直线l1在l2 上方部分的点的横坐标 一元一次不等式k1x+b1>k2x+b2的解集;
(3)直线l1在l2 下方部分的点的横坐标 一元一次不等式k1x+b1<k2x+b2的解集;
CONTENTS
3
1.(沈阳中考)在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示,当甲车出发 h时,两车相距350 km.?
2.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为 米.?
2200
3.某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
解:(1)由题意可得:
银卡消费:y=10x+150,普通票消费:y=20x.
(2)在同一坐标系中,若三种消费方式对应的函数图像如图所示,请求出点A,B,C的坐标;
当10x+150=20x时,解得x=15,则y=300,故B(15,300),
当y=10x+150,x=0时,y=150,故A(0,150),
当y=10x+150=600时,解得x=45,则y=600,故C(45,600).
(3)请根据函数图像,直接写出选择哪种消费方式更合算.
如图所示,由A,B,C的坐标可得:
当0
当15
4.联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.
(1)分别表示出y1与x,y2与x的函数关系式;
(2)月通话时间为多长时,A,B两种套餐收费一样?
(3)什么情况下A套餐更省钱?
解:(1)A套餐的收费方式:y1=0.1x+15;B套餐的收费方式:y2=0.15x.
(2)由0.1x+15=0.15x,得x=300,即当月通话时间是300分钟时,A,B两种套餐收费一样.
(3)当月通话时间多于300分钟时,A套餐更省钱.
解:(1)设购买甲种鱼苗x尾,乙种鱼苗y尾,
根据题意可得 解得
即购买甲种鱼苗500尾,乙种鱼苗200尾.
5.我市某养殖场计划购买甲、乙两种鱼苗共700尾,甲种鱼苗每尾3元,乙种鱼苗每尾5元,相关资料表明:甲、乙两种鱼苗的成活率分别为85%和90%.
(1)若购买这两种鱼苗共用去2500元,则甲、乙两种鱼苗各购买多少尾?
(2)若要使这批鱼苗的总成活率不低于88%,则甲种鱼苗至多购买多少尾?
解:设购买甲种鱼苗z尾,乙种鱼苗(700-z)尾,
列不等式得85%z+90%(700-z)≥700×88%,
解得z≤280.即甲种鱼苗至多购买280尾.
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的费用最低?并求出最低费用.
解:设甲种鱼苗购买m尾,购买鱼苗的费用为w元,
则w=3m+5(700-m)=-2m+3500,
∵-2<0,∴w随m的增大而减小,
∵0
∴700-m=420.
即当选购甲种鱼苗280尾,乙种鱼苗420尾时,总费用最低,最低费用为2940元.
CONTENTS
4
三个“一次”的关系
从“数”看一次函数y1=k1x+b1,y2=k2x+b2
(1)函数值y1=y2时x的值 一元一次方程k1x+b1=k2x+b2的解;
(2)函数值y1>y2时x的值 一元一次不等式k1x+b1>k2x+b2的解集;
(3)函数值y1<y2时x的值 一元一次不等式k1x+b1<k2x+b2的解集;
从“形”看一次函数y1=k1x+b1(直线l1),y2=k2x+b2(直线l2)
(1)直线l1与l2 交点的横坐标 一元一次方程k1x+b1=k2x+b2的解;
(2)直线l1在l2 上方部分的点的横坐标 一元一次不等式k1x+b1>k2x+b2的解集;
(3)直线l1在l2 下方部分的点的横坐标 一元一次不等式k1x+b1<k2x+b2的解集;
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
