22.1 第2课时 平行四边形的性质定理2 优质课件(23张PPT)
文档属性
| 名称 | 22.1 第2课时 平行四边形的性质定理2 优质课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 14:39:21 | ||
图片预览






文档简介
第二十二章 四边形
22.1 平行四边形的性质
第2课时 平行四边形的性质定理2
1
CONTENTS
1
想一想:
小明用几根小棒搭成一个有两条对角线的平行四边形,他先找到一根长6 cm与一根长8 cm的小棒作为平行四边形的两条对角线,然后他又找到了长分别为5 cm,8 cm,12 cm的三种小木棒,其中有几种小棒可以用来作为平行四边形的边?为什么?你自己动手搭一搭,如果一根小棒可以用来作为这个平行四边形的一边,那么它的长度应该在什么范围内?
CONTENTS
2
平行四边形的性质定理2
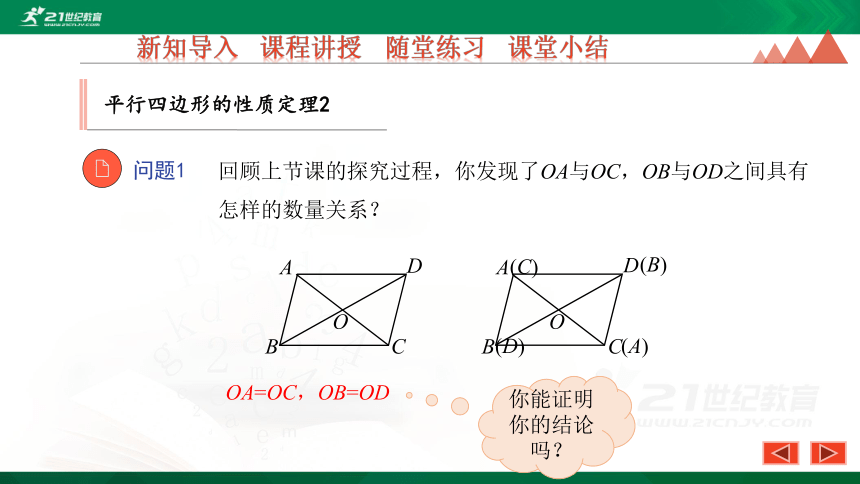
问题1
回顾上节课的探究过程,你发现了OA与OC,OB与OD之间具有怎样的数量关系?
A
D
C
B
O
A
D
C
B
O
(C)
(B)
(A)
(D)
OA=OC,OB=OD
你能证明你的结论吗?
平行四边形的性质定理2
已知:如图所示,在?ABCD中,对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
A
D
C
B
O
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAO=∠DCO.
又∵∠AOB=∠COD,
∴△AOB≌△COD.
∴OA=OC,OB=OD.
平行四边形的性质定理2
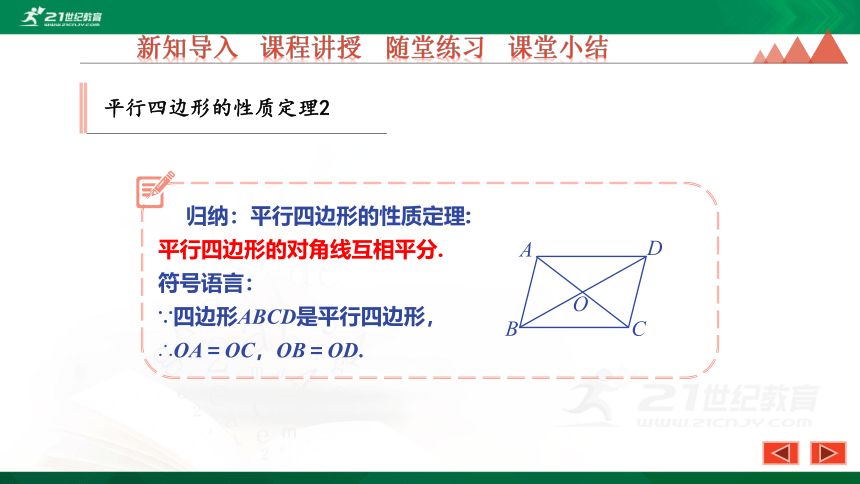
归纳:平行四边形的性质定理:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
A
D
C
B
O
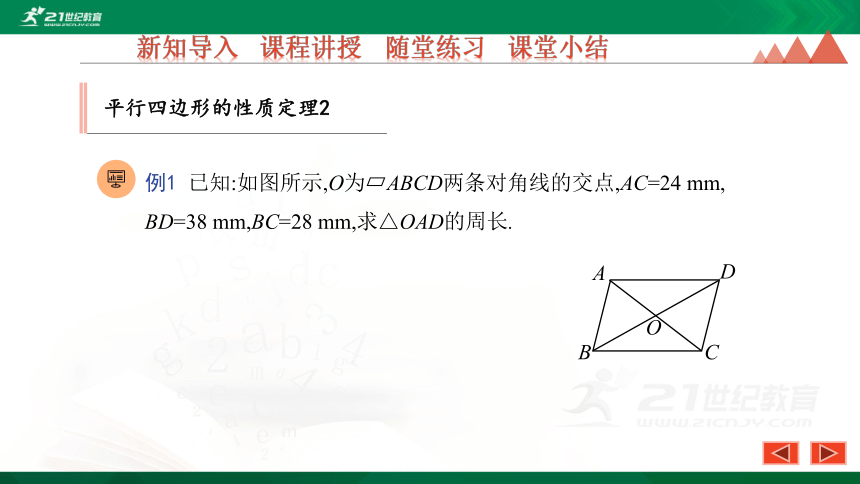
例1 已知:如图所示,O为?ABCD两条对角线的交点,AC=24 mm,
BD=38 mm,BC=28 mm,求△OAD的周长.
平行四边形的性质定理2
A
D
C
B
O
平行四边形的性质定理2
解:在?ABCD中,
∵AC=24 mm,BD=38 mm,
又∵BC=28 mm.
∴AD=BC=28 mm.
∴△OAD的周长=AO+OD+AD=12+19+28=59(mm).
A
D
C
B
O
例2 已知:如图所示,在?ABCD中,对角线AC,BD相交于点O,直线EF过点O,交DA于点E,交BC于点F.
求证:OE=OF,AE=CF,DE=BF.
平行四边形的性质定理2
A
D
C
B
O
E
F
平行四边形的性质定理2
证明:∵四边形ABCD是平行四边形,且对角线AC与BD相交于点O,
∴OA=OC,∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF.
∴OE=OF,AE=CF.
又∵AD=CB,
∴DE=AD-AE=CB-CF=BF.
A
D
C
B
O
E
F
平行四边形的性质定理2
归纳:重要结论 :在?ABCD中
1. △ABO≌ △CDO,
△AOD ≌ △COB,
△ ABD ≌ △CDB,
△ ABC ≌ △CDA ;
2. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
平行四边形的性质定理2
练一练:如图,? ABCD 的两条对角线AC、BD相交于点O,过点O的直线与AD、BC分别相交于点E、F,已知? ABCD 的面积是12cm2,则图中阴影部分的面积是 .
6 cm2
CONTENTS
3
1.(中考·眉山)如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14
B.13
C.12
D.10
C
2.如图,在?ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,则下列结论:
①CF=AE;
②OE=OF;
③DE=BF;
④图中共有四对全等三角形.
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
B
3.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
4.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为2×(BC+CD)=20.
CONTENTS
4
平行四边形
对角线的性质
对角线互相平分
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.1 平行四边形的性质
第2课时 平行四边形的性质定理2
1
CONTENTS
1
想一想:
小明用几根小棒搭成一个有两条对角线的平行四边形,他先找到一根长6 cm与一根长8 cm的小棒作为平行四边形的两条对角线,然后他又找到了长分别为5 cm,8 cm,12 cm的三种小木棒,其中有几种小棒可以用来作为平行四边形的边?为什么?你自己动手搭一搭,如果一根小棒可以用来作为这个平行四边形的一边,那么它的长度应该在什么范围内?
CONTENTS
2
平行四边形的性质定理2
问题1
回顾上节课的探究过程,你发现了OA与OC,OB与OD之间具有怎样的数量关系?
A
D
C
B
O
A
D
C
B
O
(C)
(B)
(A)
(D)
OA=OC,OB=OD
你能证明你的结论吗?
平行四边形的性质定理2
已知:如图所示,在?ABCD中,对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
A
D
C
B
O
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAO=∠DCO.
又∵∠AOB=∠COD,
∴△AOB≌△COD.
∴OA=OC,OB=OD.
平行四边形的性质定理2
归纳:平行四边形的性质定理:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
A
D
C
B
O
例1 已知:如图所示,O为?ABCD两条对角线的交点,AC=24 mm,
BD=38 mm,BC=28 mm,求△OAD的周长.
平行四边形的性质定理2
A
D
C
B
O
平行四边形的性质定理2
解:在?ABCD中,
∵AC=24 mm,BD=38 mm,
又∵BC=28 mm.
∴AD=BC=28 mm.
∴△OAD的周长=AO+OD+AD=12+19+28=59(mm).
A
D
C
B
O
例2 已知:如图所示,在?ABCD中,对角线AC,BD相交于点O,直线EF过点O,交DA于点E,交BC于点F.
求证:OE=OF,AE=CF,DE=BF.
平行四边形的性质定理2
A
D
C
B
O
E
F
平行四边形的性质定理2
证明:∵四边形ABCD是平行四边形,且对角线AC与BD相交于点O,
∴OA=OC,∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF.
∴OE=OF,AE=CF.
又∵AD=CB,
∴DE=AD-AE=CB-CF=BF.
A
D
C
B
O
E
F
平行四边形的性质定理2
归纳:重要结论 :在?ABCD中
1. △ABO≌ △CDO,
△AOD ≌ △COB,
△ ABD ≌ △CDB,
△ ABC ≌ △CDA ;
2. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
平行四边形的性质定理2
练一练:如图,? ABCD 的两条对角线AC、BD相交于点O,过点O的直线与AD、BC分别相交于点E、F,已知? ABCD 的面积是12cm2,则图中阴影部分的面积是 .
6 cm2
CONTENTS
3
1.(中考·眉山)如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14
B.13
C.12
D.10
C
2.如图,在?ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,则下列结论:
①CF=AE;
②OE=OF;
③DE=BF;
④图中共有四对全等三角形.
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
B
3.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
4.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为2×(BC+CD)=20.
CONTENTS
4
平行四边形
对角线的性质
对角线互相平分
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
