22.7 多边形的内角和与外角和 优质课件(32张PPT)
文档属性
| 名称 | 22.7 多边形的内角和与外角和 优质课件(32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 14:57:33 | ||
图片预览






文档简介
第二十二章 四边形
22.7 多边形的内角和与外角和
1
2
3
CONTENTS
1
想一想:
在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到由一些线段围成的图形吗?
CONTENTS
2
多边形的有关概念
问题1.1
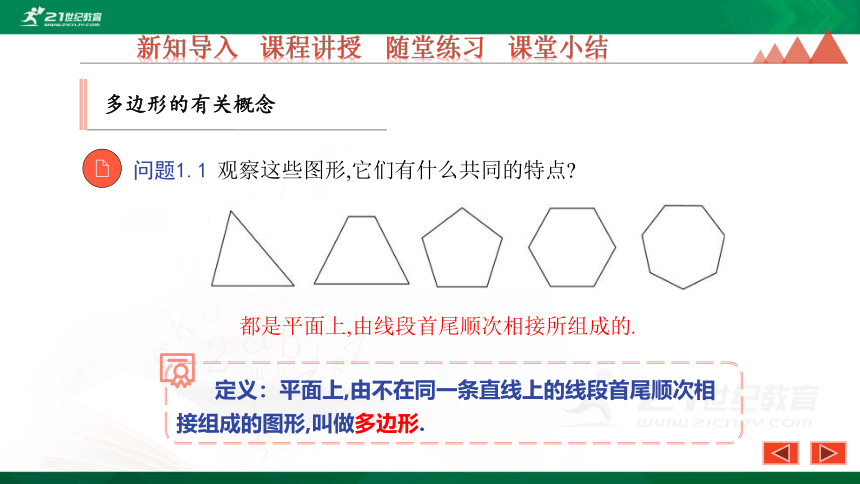
观察这些图形,它们有什么共同的特点?
都是平面上,由线段首尾顺次相接所组成的.
定义:平面上,由不在同一条直线上的线段首尾顺次相接组成的图形,叫做多边形.
多边形的有关概念
问题1.2
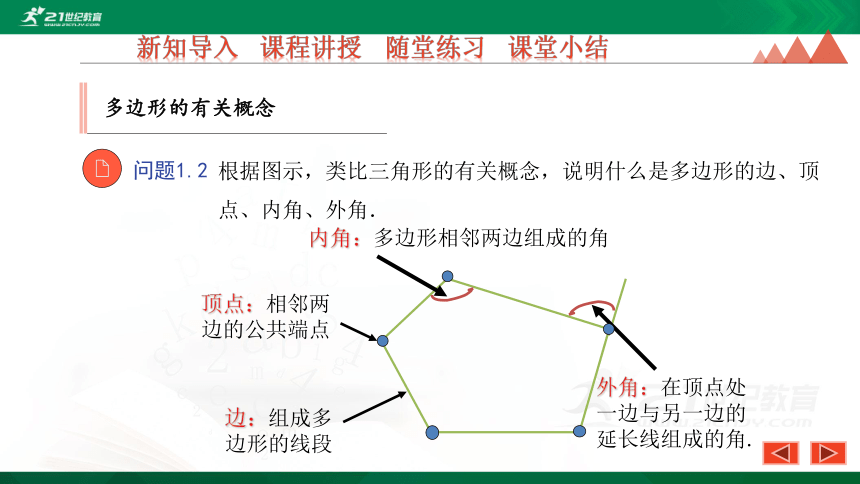
根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
内角:多边形相邻两边组成的角
顶点:相邻两边的公共端点
边:组成多边形的线段
外角:在顶点处一边与另一边的延长线组成的角.
多边形的有关概念
A
B
C
D
E
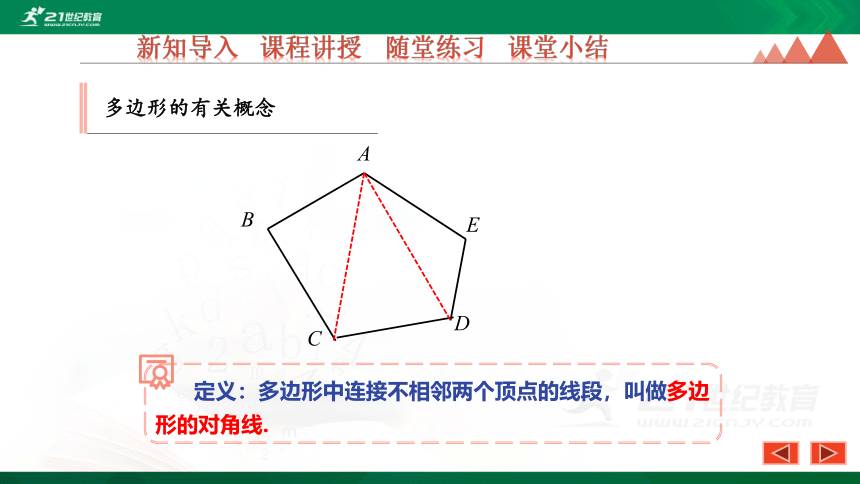
定义:多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
多边形的有关概念
问题1.3
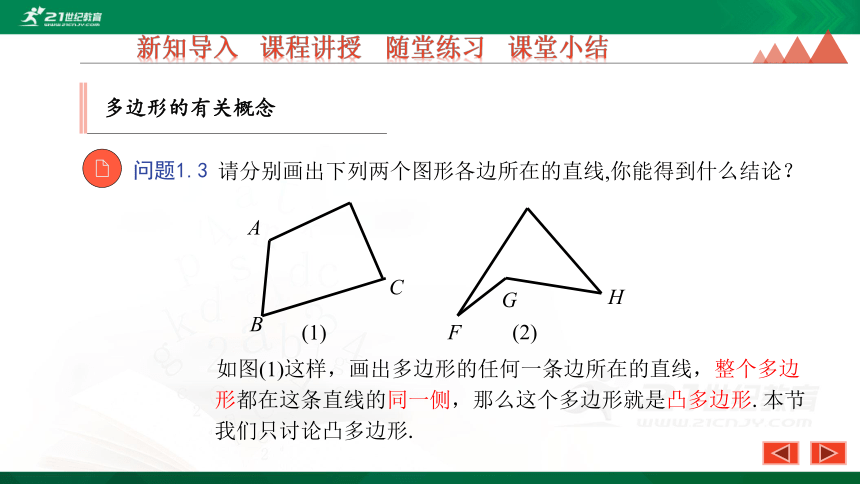
请分别画出下列两个图形各边所在的直线,你能得到什么结论?
(1)
(2)
A
B
C
F
G
H
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.本节我们只讨论凸多边形.
多边形的内角和
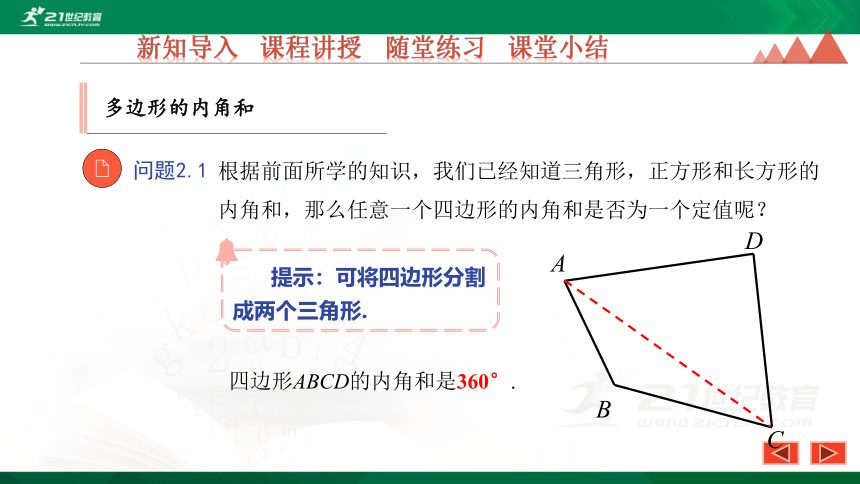
问题2.1
根据前面所学的知识,我们已经知道三角形,正方形和长方形的内角和,那么任意一个四边形的内角和是否为一个定值呢?
A
B
C
D
提示:可将四边形分割成两个三角形.
四边形ABCD的内角和是360°.
多边形的内角和
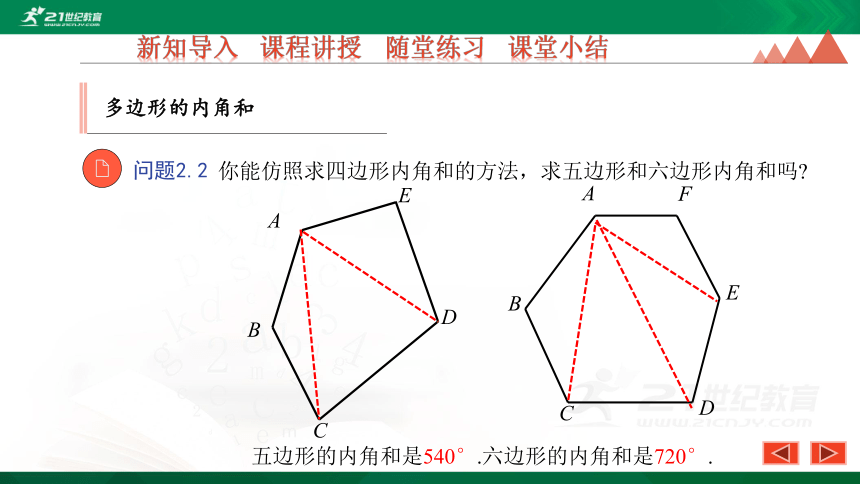
问题2.2
你能仿照求四边形内角和的方法,求五边形和六边形内角和吗?
A
C
D
E
B
A
B
C
D
E
F
五边形的内角和是540°.六边形的内角和是720°.
多边形的内角和
问题2.3
根据分割多边形的方法,你能试着归纳出多边形内角和的公式吗?并将结果填入下表.
从n边形的一个顶点出发,向自身和相邻的两个顶点无法引对角线,向其他顶点共引(n-3)条对角线,这时n边形被分割成(n-2)个三角形,因为每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°(n≥3).
多边形的内角和
多边形
图形(分割成三角形)
分割出的三角形的个数
多边形的
内角和
四边形
五边形
六边形
n边形
2
3
4
n-2
360°
540°
720°
(n-2)×180°
多边形的内角和
归纳:多边形的内角和定理
n边形的内角和为(n-2)×180°(n≥3).
多边形的内角和
练一练:如图为缅甸发行的六边形硬币,其内角和为( )
A.540°
B.720°
C.900°
D.1080°
B
多边形的外角和
问题3.1
在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.任意一个外角和它相邻的内角有什么关系?
E
B
C
D
1
2
3
4
5
A
任意一个外角和它相邻的内角互补.
多边形的外角和
问题3.2
在五边形中,五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
5×180°=900°
多边形的外角和
问题3.3
在五边形中,这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
五边形外角和
=5个平角-五边形内角和
=5×180°-(5-2)×180°
=360 °
多边形的外角和
问题3.4
如果将前面问题中的五边形换成n边形(n是不小于3的任意整数),可以得到同样的结果吗?
An
A2
A3
A4
1
2
3
4
n
A1
n边形外角和
=n个平角-n边形内角和
= n×180 °-(n-2) × 180°
=360 °
归纳:多边形的外角和定理:多边形的外角和等于360°
例1 已知一个多边形,它的内角和与外角和相等,这个多边形是几边形?
多边形的外角和
解:设多边形的边数是n,那么它的内角和等于(n-2)×180°,
外角和等于360°,
由题意,得(n-2)×180°=360°.
解这个方程,得n=4.
所以,这个多边形是四边形.
多边形的外角和
例2 如图所示,小亮从点O处出发,前进5 m后向右转20°,再前进5 m后又向右转20°,这样走n次后恰好回到点O处.
(1)小亮走出的这个n边形的每个内角是多少度,内角和是多少度?
(2)小亮走出的这个n边形的周长是多少米?
多边形的外角和
解:(1)设这个n边形的每个内角为180°-20°=160°.
因为多边形外角和等于360°,
所以n×20°=360°.解得n=18.
所以这个n边形的内角和=(18-2)×180°=2880°.
(2)5×18=90(m),所以,小亮走出的这个n边形的周长为90 m.
CONTENTS
3
1.判断:
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
4.一个正多边形的内角和为720°,则这个正多边形的
每一个内角等于______.
120°
2.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.710 °
D
3.一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A.360° B.540 ° C.720 ° D.900 °
B
5.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,若∠1=115°,则∠2+∠3+∠4+∠5=______.
295°
6.如图,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
150
7.如图所示,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,求∠AOB的度数.
解:∵∠D+∠C+∠DAB+∠ABC=360°,
∠D+∠C=220°,
∴∠DAB+∠ABC=360°-220°=140°.
∵∠1=∠2,∠3=∠4,∴∠2+∠3=70°,
∴∠AOB=180°-70°=110°.
CONTENTS
4
多边形
定义
平面上,由不在同一条直线上的线段首尾顺次相接组成的图形,叫做多边形.
对角线
多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
内角和
(n-2) × 180 °(n ≥3的任意整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.7 多边形的内角和与外角和
1
2
3
CONTENTS
1
想一想:
在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到由一些线段围成的图形吗?
CONTENTS
2
多边形的有关概念
问题1.1
观察这些图形,它们有什么共同的特点?
都是平面上,由线段首尾顺次相接所组成的.
定义:平面上,由不在同一条直线上的线段首尾顺次相接组成的图形,叫做多边形.
多边形的有关概念
问题1.2
根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
内角:多边形相邻两边组成的角
顶点:相邻两边的公共端点
边:组成多边形的线段
外角:在顶点处一边与另一边的延长线组成的角.
多边形的有关概念
A
B
C
D
E
定义:多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
多边形的有关概念
问题1.3
请分别画出下列两个图形各边所在的直线,你能得到什么结论?
(1)
(2)
A
B
C
F
G
H
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.本节我们只讨论凸多边形.
多边形的内角和
问题2.1
根据前面所学的知识,我们已经知道三角形,正方形和长方形的内角和,那么任意一个四边形的内角和是否为一个定值呢?
A
B
C
D
提示:可将四边形分割成两个三角形.
四边形ABCD的内角和是360°.
多边形的内角和
问题2.2
你能仿照求四边形内角和的方法,求五边形和六边形内角和吗?
A
C
D
E
B
A
B
C
D
E
F
五边形的内角和是540°.六边形的内角和是720°.
多边形的内角和
问题2.3
根据分割多边形的方法,你能试着归纳出多边形内角和的公式吗?并将结果填入下表.
从n边形的一个顶点出发,向自身和相邻的两个顶点无法引对角线,向其他顶点共引(n-3)条对角线,这时n边形被分割成(n-2)个三角形,因为每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°(n≥3).
多边形的内角和
多边形
图形(分割成三角形)
分割出的三角形的个数
多边形的
内角和
四边形
五边形
六边形
n边形
2
3
4
n-2
360°
540°
720°
(n-2)×180°
多边形的内角和
归纳:多边形的内角和定理
n边形的内角和为(n-2)×180°(n≥3).
多边形的内角和
练一练:如图为缅甸发行的六边形硬币,其内角和为( )
A.540°
B.720°
C.900°
D.1080°
B
多边形的外角和
问题3.1
在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.任意一个外角和它相邻的内角有什么关系?
E
B
C
D
1
2
3
4
5
A
任意一个外角和它相邻的内角互补.
多边形的外角和
问题3.2
在五边形中,五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
5×180°=900°
多边形的外角和
问题3.3
在五边形中,这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
五边形外角和
=5个平角-五边形内角和
=5×180°-(5-2)×180°
=360 °
多边形的外角和
问题3.4
如果将前面问题中的五边形换成n边形(n是不小于3的任意整数),可以得到同样的结果吗?
An
A2
A3
A4
1
2
3
4
n
A1
n边形外角和
=n个平角-n边形内角和
= n×180 °-(n-2) × 180°
=360 °
归纳:多边形的外角和定理:多边形的外角和等于360°
例1 已知一个多边形,它的内角和与外角和相等,这个多边形是几边形?
多边形的外角和
解:设多边形的边数是n,那么它的内角和等于(n-2)×180°,
外角和等于360°,
由题意,得(n-2)×180°=360°.
解这个方程,得n=4.
所以,这个多边形是四边形.
多边形的外角和
例2 如图所示,小亮从点O处出发,前进5 m后向右转20°,再前进5 m后又向右转20°,这样走n次后恰好回到点O处.
(1)小亮走出的这个n边形的每个内角是多少度,内角和是多少度?
(2)小亮走出的这个n边形的周长是多少米?
多边形的外角和
解:(1)设这个n边形的每个内角为180°-20°=160°.
因为多边形外角和等于360°,
所以n×20°=360°.解得n=18.
所以这个n边形的内角和=(18-2)×180°=2880°.
(2)5×18=90(m),所以,小亮走出的这个n边形的周长为90 m.
CONTENTS
3
1.判断:
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
4.一个正多边形的内角和为720°,则这个正多边形的
每一个内角等于______.
120°
2.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.710 °
D
3.一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A.360° B.540 ° C.720 ° D.900 °
B
5.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,若∠1=115°,则∠2+∠3+∠4+∠5=______.
295°
6.如图,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
150
7.如图所示,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,求∠AOB的度数.
解:∵∠D+∠C+∠DAB+∠ABC=360°,
∠D+∠C=220°,
∴∠DAB+∠ABC=360°-220°=140°.
∵∠1=∠2,∠3=∠4,∴∠2+∠3=70°,
∴∠AOB=180°-70°=110°.
CONTENTS
4
多边形
定义
平面上,由不在同一条直线上的线段首尾顺次相接组成的图形,叫做多边形.
对角线
多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
内角和
(n-2) × 180 °(n ≥3的任意整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
