29.3 切线的性质和判定 优质课件(30张PPT)
文档属性
| 名称 | 29.3 切线的性质和判定 优质课件(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 14:19:04 | ||
图片预览










文档简介
29.3 切线的性质和判定
第二十九章 直线与圆的位置关系
1
2
CONTENTS
1
看一看:观察下图中图形,试着发现它们的规律.
CONTENTS
2
切线的性质
问题1 前面我们已学过的切线的性质有哪些?
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
想一想:切线还有什么性质?
切线的性质
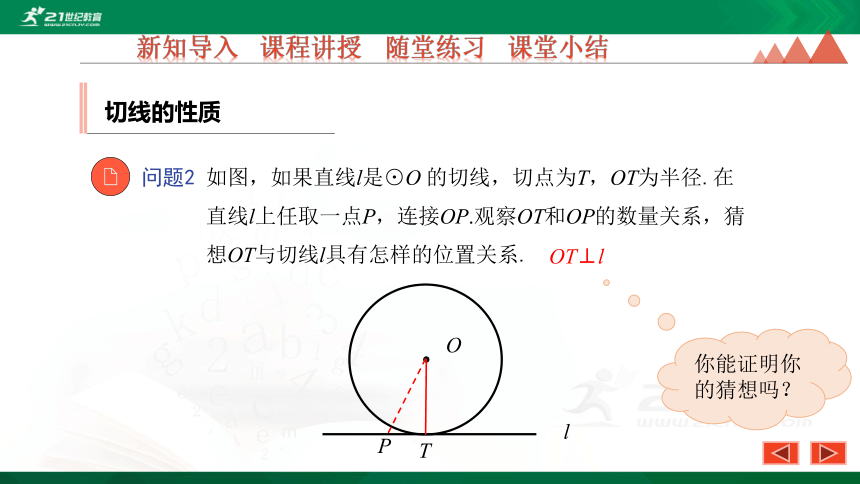
问题2 如图,如果直线l是⊙O 的切线,切点为T,OT为半径.在
直线l上任取一点P,连接OP.观察OT和OP的数量关系,猜
想OT与切线l具有怎样的位置关系.
P
O
l
T
OT⊥l
你能证明你的猜想吗?
切线的性质
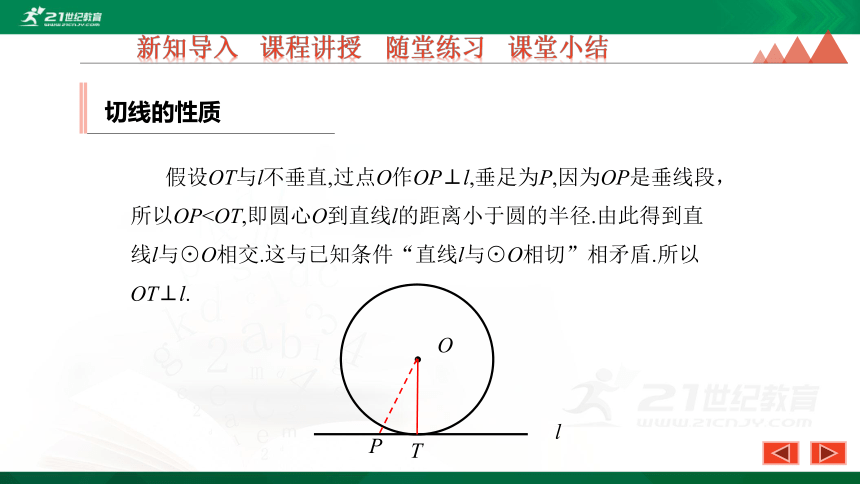
假设OT与l不垂直,过点O作OP⊥l,垂足为P,因为OP是垂线段,所以OPP
O
l
T
切线的性质
归纳:圆的切线垂直于过切点的半径.
切线的判定
归纳:圆的切线垂直于过切点的半径.
经过圆心且垂直于切线的直线必经过切点.
经过切点且垂直于切线的直线必经过圆心.
经过圆心
直线经过切点
垂直于切线
知二推一
切线的性质
练一练:如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交
⊙O于点C,连接BC,若∠P=36°,则∠B等于( )
A.27°
B.32°
C.36°
D.54°
A
切线的判定
问题1 如图, OA为⊙O的半径,直线l过点 A ,且l⊥OA,
(1)如果用r表示⊙O半径的长,d表示圆心O到直线l的距离,那
么r与d具有怎样的数量关系呢?
(2)直线 l 是⊙O的切线吗?
O
l
A
直线 l 与⊙O相切.
d=r
切线的判定
归纳:经过半径的外端并且垂直与这条半径的直线是
圆的切线.
几何符号表达:
∵ OA是半径,OA⊥l于点A
∴ l是⊙O的切线.
切线的判定
归纳:切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即经过半径的外端并且垂
直这条半径的直线是圆的切线.
切线的判定
例1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
O
B
A
C
证明:连接OC(如图).
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径
∴ AB是⊙O的切线.
切线的判定
例2 已知:O为∠BAC平分线上一点,OD⊥AB于点D,以点O为
圆心,OD为半径作⊙O.
求证:⊙O与AC相切.
O
A
B
C
D
证明:过点O作OE⊥AC于点E.
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线.
E
切线的判定
归纳:常用的添辅助线方法
⑴直线与圆的公共点已知时,作出过公共点的半径,
再证半径垂直于该直线.(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线
段,再证明这条垂线段等于圆的半径.(作垂直,
证半径)
切线的判定
练一练:下列四个命题:
①与圆有公共点的直线是圆的切线;
②垂直于圆的半径的直线是圆的切线;
③到圆心的距离等于半径的直线是圆的切线;
④过直径的端点,且垂直于此直径的直线是
圆的切线.其中真命题是( )
A.①② B.②③
C.③④ D.①④
C
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这条半径垂直。
切线的画法
问题1 如图,P为⊙O上的一点,请你用三角尺画出这个圆过点P切线.
l
O
P
1.连接OP
2.过点P画l⊥OP,直线l为所画
CONTENTS
3
1.如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )
A.3
B.3
C.6
D.9
A
2.如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
A.30°
B.35°
C.40°
D.45°
D
3.如图,在⊙O中,AB=OA,P是半径OB延长线上一点,且PB=OB,PA与⊙O的位置关系是________.
相切
4.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙O的半径为_________.
2.4
5.如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
∴CD为⊙O的切线.
证明: ∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,
∴OC⊥CD,
6.如图,在△ABC中,AB=AC,AB是直径,BC与⊙O相交于点D,DE切⊙O于点D.
求证:DE⊥AC.
∴DE⊥AC.
证明: 连接OD.
∵DE是⊙O的切线,
∴DO⊥DE.
∵OB=OD,
∴∠B=∠BDO.
∵AB=AC,
∴∠B=∠C,
∴∠BDO=∠C,
∴OD∥AC,
CONTENTS
4
切线的性质和判定
切线的性质
切线的判定
经过切点且垂直于切线的直线必过圆心
经过圆心且垂直于切线的直线必过切点
圆的切线垂直于过切点的半径
数量法d=r
判定定理
定义法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第二十九章 直线与圆的位置关系
1
2
CONTENTS
1
看一看:观察下图中图形,试着发现它们的规律.
CONTENTS
2
切线的性质
问题1 前面我们已学过的切线的性质有哪些?
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
想一想:切线还有什么性质?
切线的性质
问题2 如图,如果直线l是⊙O 的切线,切点为T,OT为半径.在
直线l上任取一点P,连接OP.观察OT和OP的数量关系,猜
想OT与切线l具有怎样的位置关系.
P
O
l
T
OT⊥l
你能证明你的猜想吗?
切线的性质
假设OT与l不垂直,过点O作OP⊥l,垂足为P,因为OP是垂线段,所以OP
O
l
T
切线的性质
归纳:圆的切线垂直于过切点的半径.
切线的判定
归纳:圆的切线垂直于过切点的半径.
经过圆心且垂直于切线的直线必经过切点.
经过切点且垂直于切线的直线必经过圆心.
经过圆心
直线经过切点
垂直于切线
知二推一
切线的性质
练一练:如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交
⊙O于点C,连接BC,若∠P=36°,则∠B等于( )
A.27°
B.32°
C.36°
D.54°
A
切线的判定
问题1 如图, OA为⊙O的半径,直线l过点 A ,且l⊥OA,
(1)如果用r表示⊙O半径的长,d表示圆心O到直线l的距离,那
么r与d具有怎样的数量关系呢?
(2)直线 l 是⊙O的切线吗?
O
l
A
直线 l 与⊙O相切.
d=r
切线的判定
归纳:经过半径的外端并且垂直与这条半径的直线是
圆的切线.
几何符号表达:
∵ OA是半径,OA⊥l于点A
∴ l是⊙O的切线.
切线的判定
归纳:切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即经过半径的外端并且垂
直这条半径的直线是圆的切线.
切线的判定
例1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
O
B
A
C
证明:连接OC(如图).
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径
∴ AB是⊙O的切线.
切线的判定
例2 已知:O为∠BAC平分线上一点,OD⊥AB于点D,以点O为
圆心,OD为半径作⊙O.
求证:⊙O与AC相切.
O
A
B
C
D
证明:过点O作OE⊥AC于点E.
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线.
E
切线的判定
归纳:常用的添辅助线方法
⑴直线与圆的公共点已知时,作出过公共点的半径,
再证半径垂直于该直线.(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线
段,再证明这条垂线段等于圆的半径.(作垂直,
证半径)
切线的判定
练一练:下列四个命题:
①与圆有公共点的直线是圆的切线;
②垂直于圆的半径的直线是圆的切线;
③到圆心的距离等于半径的直线是圆的切线;
④过直径的端点,且垂直于此直径的直线是
圆的切线.其中真命题是( )
A.①② B.②③
C.③④ D.①④
C
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这条半径垂直。
切线的画法
问题1 如图,P为⊙O上的一点,请你用三角尺画出这个圆过点P切线.
l
O
P
1.连接OP
2.过点P画l⊥OP,直线l为所画
CONTENTS
3
1.如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )
A.3
B.3
C.6
D.9
A
2.如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
A.30°
B.35°
C.40°
D.45°
D
3.如图,在⊙O中,AB=OA,P是半径OB延长线上一点,且PB=OB,PA与⊙O的位置关系是________.
相切
4.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙O的半径为_________.
2.4
5.如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
∴CD为⊙O的切线.
证明: ∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,
∴OC⊥CD,
6.如图,在△ABC中,AB=AC,AB是直径,BC与⊙O相交于点D,DE切⊙O于点D.
求证:DE⊥AC.
∴DE⊥AC.
证明: 连接OD.
∵DE是⊙O的切线,
∴DO⊥DE.
∵OB=OD,
∴∠B=∠BDO.
∵AB=AC,
∴∠B=∠C,
∴∠BDO=∠C,
∴OD∥AC,
CONTENTS
4
切线的性质和判定
切线的性质
切线的判定
经过切点且垂直于切线的直线必过圆心
经过圆心且垂直于切线的直线必过切点
圆的切线垂直于过切点的半径
数量法d=r
判定定理
定义法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
