30.2 第1课时 二次函数y=ax2的图像和性质 优质课件(30张PPT)
文档属性
| 名称 | 30.2 第1课时 二次函数y=ax2的图像和性质 优质课件(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览










文档简介
第三十章 二次函数
30.2 二次函数的图像和性质
第1课时 二次函数y=ax2的图像和性质
1
2
CONTENTS
1
看一看:
观察下列运动,试着发现它们的规律
CONTENTS
2
二次函数y=ax2的图像
问题1.1 一次函数、反比例函数的图像分别是什么形状?
一条直线、双曲线
列表、描点、连线
问题1.2 画函数图像的基本步骤是什么?
二次函数y=ax2的图像
问题1.3 探究一次函数、反比例函数的性质的基本思路是怎样的?
问题1.4 类比探究一次函数、反比例函数性质的思路来研究二次函数的性质,所以我们应该先探究什么内容?
先画出一次函数的图像,然后观察、分析、归纳得到一次函数的性质
先画出二次函数的图像
-1
-2
-3
9
3
6
1
2
3
y
O
x
二次函数y=ax2的图像
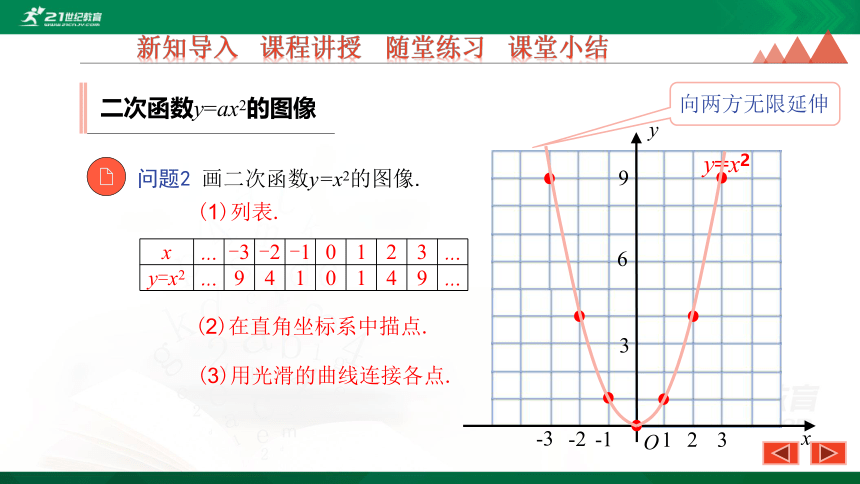
问题2 画二次函数y=x2的图像.
y=x2
(1)列表.
(2)在直角坐标系中描点.
(3)用光滑的曲线连接各点.
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
向两方无限延伸
二次函数y=ax2的图像
想一想:观察二次函数y=x2的图像,回答下列问题:
(1)若将y=x2的图像沿着y轴对折,y轴两侧的部分能够完全重合吗?y=x2的图像是不是轴对称图形?如果是,那么它的对称轴是哪条直线?
(2)函数y=x2的图像有最低点吗?如果有,那么最低点的坐标是什么?
能够完全重合,是轴对称图形,对称轴是y轴
y=x2的图像有最低点,最低点的坐标是(0,0)
二次函数y=ax2的图像
定义:二次函数y=ax2的图像是一条关于y轴对称的曲线,这样的曲线叫做抛物线,曲线的对称轴叫做抛物线的对称轴,抛物线与它的对称轴的交点叫做抛物线的顶点.
二次函数y=ax2的性质
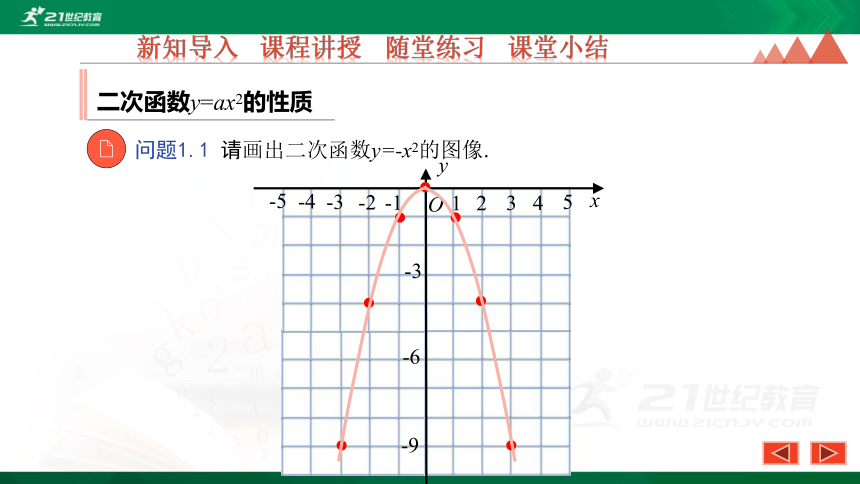
问题1.1 请画出二次函数y=-x2的图像.
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
二次函数y=ax2的性质
问题1.2 在如图所示的直角坐标系中,
已画出了y=2x2的图像,请再画
出函数y=-2x2的图像.
二次函数y=ax2的性质
想一想:对比函数y=x2与y=-x2,y=2x2与y=-2x2的图像,就二次函数y=ax2回答以下问题:
(1)图像的开口方向和它的最高(或最低)点与a的符号具有怎样的关系?
(2)图像是不是轴对称图形?如果是,那么它的对称轴是哪条直线?
(3)根据图像,说明y的值随x的值增大而变化的情况.
二次函数y=ax2的性质
二次函数y=ax2的图像和性质:
表达式
开口方向
对称轴
顶点坐标
y随x的变化情况
最大(或最小)值
y=ax2
(a>0)
y=ax2
(a<0)
向上
向下
y轴
y轴
原点
(0,0)
原点
(0,0)
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小
有最低点(0,0).当x=0时,y最小=0
有最高点(0,0).当x=0时,y最大=0
二次函数y=ax2的性质
问题2.1 在同一直角坐标系中,画出函数 的图像.
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
…
…
y=2x2
…
…
9
4
1
0
1
9
4
2
0.5
0
4.5
2
0.5
4.5
8
2
0
8
0.5
18
18
二次函数y=ax2的性质
-1
-2
-3
9
3
6
1
2
3
y
O
x
y=x2
y=2x2
当a>0时,a越大,开口越小.
二次函数y=ax2的性质
问题2.2 在同一直角坐标系中,画出函数 的图像.
x
…
-3
-2
-1
0
1
2
3
…
y=-x2
…
…
…
…
y=-2x2
…
…
-9
-4
-1
0
-1
-9
-4
-2
-0.5
0
-4.5
-2
-0.5
-4.5
-8
-2
0
-8
-0.5
-18
-18
二次函数y=ax2的性质
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
y=-x2
y=-2x2
当a<0时,a越大,开口越大.
二次函数y=ax2的性质
归纳:抛物线y=ax2中的系数a决定抛物线的开口方向和大小,当|a|越大时,抛物线的开口越小;当|a|越小时,抛物线的开口越大.
二次函数y=ax2的性质
练一练:抛物线y=2x2,y=-2x2,y=x2的共同性质是( )
A.开口向上
B.对称轴是y轴
C.都有最高点
D.y随x的增大而增大
B
CONTENTS
3
1.若点(x1,y1),(x2,y2)是二次函数y=-4x2图像上两点,且x1>x2>0,则y1与y2的大小关系是( )
A.y1>y2 B.y1<y2
C.y1≥y2 D.y1≤y2
2.已知抛物线y=ax2(a>0)过点A(-2,y1),点B(1,y2),则下列关系式一定成立的是( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y1≤y2
B
C
3.如图,从y=-x2的图像上可看出当-3A.-9B.-9≤y<-1
C.-9≤y≤0
D.-9D
4.如图,在同一坐标系中,作出①y=3x2,②y= x2,③y=x2的图像,则图像中从里到外的三条抛物线对应的函数依次是____________.(填序号)
①③②
5.二次函数y=ax2的图像如图所示.
(1)求这个二次函数表达式;
(2)若另一函数图像与该函数图像关于x轴对称,试求另一个函数的表达式.
解: (1)因为图像经过(2,2),代入表达式,
得a= ,
2
1
y=- x2.
2
1
故所求的表达式为y= x2.
2
1
(2)由题意得另一个函数的表达式为
6.二次函数y=ax2的图像与直线y=2x-1相交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的表达式,并指出x取何值时,该表达式的y随x的增大而增大;
(3)指出抛物线的顶点坐标和对称轴.
(3)顶点坐标为(0,0),对称轴为y轴.
解: (1)将(1,m)代入y=2x-1,
得m=2×1-1=1.
所以点P的坐标为(1,1),
将点P的坐标(1,1)代入y=ax2,得
1=a×12,
解得a=1.
(2)二次函数的表达式为y=x2,
当x>0时,y随x的增大而增大.
CONTENTS
4
二次函数y=ax2的图像及性质
图像及性质
对于抛物线 y = ax 2 (a>0),开口向上
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
对于抛物线 y = ax 2 (a<0),开口向下
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
特性
对于抛物线 y = ax 2 ,|a|越大,抛物线的开口越小.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
30.2 二次函数的图像和性质
第1课时 二次函数y=ax2的图像和性质
1
2
CONTENTS
1
看一看:
观察下列运动,试着发现它们的规律
CONTENTS
2
二次函数y=ax2的图像
问题1.1 一次函数、反比例函数的图像分别是什么形状?
一条直线、双曲线
列表、描点、连线
问题1.2 画函数图像的基本步骤是什么?
二次函数y=ax2的图像
问题1.3 探究一次函数、反比例函数的性质的基本思路是怎样的?
问题1.4 类比探究一次函数、反比例函数性质的思路来研究二次函数的性质,所以我们应该先探究什么内容?
先画出一次函数的图像,然后观察、分析、归纳得到一次函数的性质
先画出二次函数的图像
-1
-2
-3
9
3
6
1
2
3
y
O
x
二次函数y=ax2的图像
问题2 画二次函数y=x2的图像.
y=x2
(1)列表.
(2)在直角坐标系中描点.
(3)用光滑的曲线连接各点.
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
向两方无限延伸
二次函数y=ax2的图像
想一想:观察二次函数y=x2的图像,回答下列问题:
(1)若将y=x2的图像沿着y轴对折,y轴两侧的部分能够完全重合吗?y=x2的图像是不是轴对称图形?如果是,那么它的对称轴是哪条直线?
(2)函数y=x2的图像有最低点吗?如果有,那么最低点的坐标是什么?
能够完全重合,是轴对称图形,对称轴是y轴
y=x2的图像有最低点,最低点的坐标是(0,0)
二次函数y=ax2的图像
定义:二次函数y=ax2的图像是一条关于y轴对称的曲线,这样的曲线叫做抛物线,曲线的对称轴叫做抛物线的对称轴,抛物线与它的对称轴的交点叫做抛物线的顶点.
二次函数y=ax2的性质
问题1.1 请画出二次函数y=-x2的图像.
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
二次函数y=ax2的性质
问题1.2 在如图所示的直角坐标系中,
已画出了y=2x2的图像,请再画
出函数y=-2x2的图像.
二次函数y=ax2的性质
想一想:对比函数y=x2与y=-x2,y=2x2与y=-2x2的图像,就二次函数y=ax2回答以下问题:
(1)图像的开口方向和它的最高(或最低)点与a的符号具有怎样的关系?
(2)图像是不是轴对称图形?如果是,那么它的对称轴是哪条直线?
(3)根据图像,说明y的值随x的值增大而变化的情况.
二次函数y=ax2的性质
二次函数y=ax2的图像和性质:
表达式
开口方向
对称轴
顶点坐标
y随x的变化情况
最大(或最小)值
y=ax2
(a>0)
y=ax2
(a<0)
向上
向下
y轴
y轴
原点
(0,0)
原点
(0,0)
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小
有最低点(0,0).当x=0时,y最小=0
有最高点(0,0).当x=0时,y最大=0
二次函数y=ax2的性质
问题2.1 在同一直角坐标系中,画出函数 的图像.
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
…
…
y=2x2
…
…
9
4
1
0
1
9
4
2
0.5
0
4.5
2
0.5
4.5
8
2
0
8
0.5
18
18
二次函数y=ax2的性质
-1
-2
-3
9
3
6
1
2
3
y
O
x
y=x2
y=2x2
当a>0时,a越大,开口越小.
二次函数y=ax2的性质
问题2.2 在同一直角坐标系中,画出函数 的图像.
x
…
-3
-2
-1
0
1
2
3
…
y=-x2
…
…
…
…
y=-2x2
…
…
-9
-4
-1
0
-1
-9
-4
-2
-0.5
0
-4.5
-2
-0.5
-4.5
-8
-2
0
-8
-0.5
-18
-18
二次函数y=ax2的性质
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
y=-x2
y=-2x2
当a<0时,a越大,开口越大.
二次函数y=ax2的性质
归纳:抛物线y=ax2中的系数a决定抛物线的开口方向和大小,当|a|越大时,抛物线的开口越小;当|a|越小时,抛物线的开口越大.
二次函数y=ax2的性质
练一练:抛物线y=2x2,y=-2x2,y=x2的共同性质是( )
A.开口向上
B.对称轴是y轴
C.都有最高点
D.y随x的增大而增大
B
CONTENTS
3
1.若点(x1,y1),(x2,y2)是二次函数y=-4x2图像上两点,且x1>x2>0,则y1与y2的大小关系是( )
A.y1>y2 B.y1<y2
C.y1≥y2 D.y1≤y2
2.已知抛物线y=ax2(a>0)过点A(-2,y1),点B(1,y2),则下列关系式一定成立的是( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y1≤y2
B
C
3.如图,从y=-x2的图像上可看出当-3
C.-9≤y≤0
D.-9
4.如图,在同一坐标系中,作出①y=3x2,②y= x2,③y=x2的图像,则图像中从里到外的三条抛物线对应的函数依次是____________.(填序号)
①③②
5.二次函数y=ax2的图像如图所示.
(1)求这个二次函数表达式;
(2)若另一函数图像与该函数图像关于x轴对称,试求另一个函数的表达式.
解: (1)因为图像经过(2,2),代入表达式,
得a= ,
2
1
y=- x2.
2
1
故所求的表达式为y= x2.
2
1
(2)由题意得另一个函数的表达式为
6.二次函数y=ax2的图像与直线y=2x-1相交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的表达式,并指出x取何值时,该表达式的y随x的增大而增大;
(3)指出抛物线的顶点坐标和对称轴.
(3)顶点坐标为(0,0),对称轴为y轴.
解: (1)将(1,m)代入y=2x-1,
得m=2×1-1=1.
所以点P的坐标为(1,1),
将点P的坐标(1,1)代入y=ax2,得
1=a×12,
解得a=1.
(2)二次函数的表达式为y=x2,
当x>0时,y随x的增大而增大.
CONTENTS
4
二次函数y=ax2的图像及性质
图像及性质
对于抛物线 y = ax 2 (a>0),开口向上
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
对于抛物线 y = ax 2 (a<0),开口向下
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
特性
对于抛物线 y = ax 2 ,|a|越大,抛物线的开口越小.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
