30.1 二次函数 优质课件(29张PPT)
文档属性
| 名称 | 30.1 二次函数 优质课件(29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览







文档简介
第三十章 二次函数
30.1 二次函数
1
2
3
CONTENTS
1
想一想:
.
以点O为圆心画圆 ,
改变半径r,圆有哪些改变?
O
CONTENTS
2
二次函数的概念
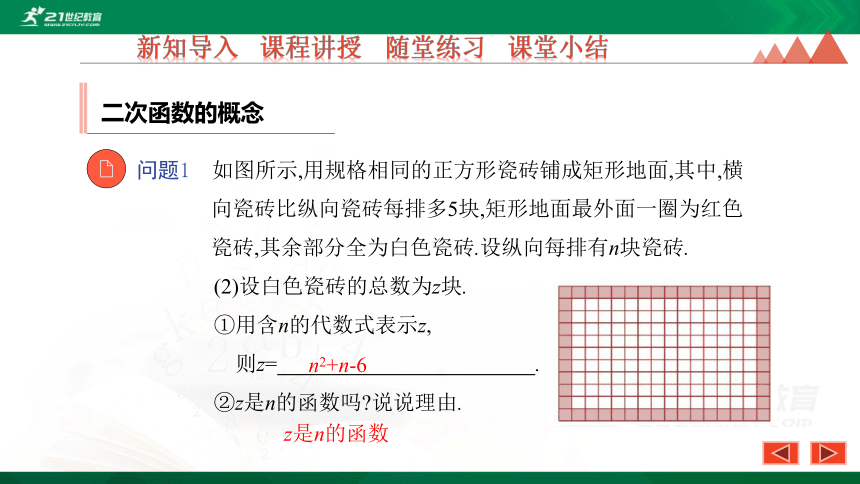
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
(1)设红色瓷砖的总数为y块.
①用含n的代数式表示y,
则y= .?
②y与n具有怎样的函数关系?
4n+6
一次函数
二次函数的概念
(2)设白色瓷砖的总数为z块.
①用含n的代数式表示z,
则z= .?
②z是n的函数吗?说说理由.
z是n的函数
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
n2+n-6
二次函数的概念
问题2 某企业今年第一季度的产值为80万元,预计产值的季平均增长率为x.
分析:
(1)设第二季度的产值为y万元,则y= .
设第三季度的产值为z万元,则z= .?
(2)y,z都是x的函数吗?它们的表达式有什么不同?
y=80x+80
z=80x2+160x+80
y=80x+80,一次函数.
z=80x2+160x+80,z是x的函数.
二次函数的概念
问题3 观察下面两个函数:z=n2+n-6,z=80x2+160x+80,
(1)这两个函数与我们学过的函数有什么不同?
(2)这两个函数的自变量x的最高指数分别是多少?
(3)你能说出函数表达式右边的二次项,一次项,常数项及二次项系数,一次项系数吗?
(4)通过观察,你能归纳出这种函数的一般形式吗?
二次函数的概念
定义:一般地,如果两个变量x和y之间的函数关系可以表示成y=ax2+bx+c(a,b,c是常数,且a≠0),那么称y为x的二次函数.其中,a叫做二次项系数,b叫做一次项系数,c叫做常数项.
二次函数的概念
想一想:(1)二次项系数能不能为0?一次项系数和常数项呢?为什么?
(2)如何判断一个函数是不是二次函数?
(3)二次函数的一般形式与一元二次方程的一般形式有什么关系?
(4)函数 是不是二次函数?
(1)函数表达式的右边是整式形式;
(2)自变量的最高指数是2;
(3)二次项系数不为0.
二次函数的概念
想一想:1.请分别指出 的二次项系数、一次项系数和常数项.
2.谈谈一次函数、反比例函数、二次函数有什么不同.
二次函数的概念
例 若y=(m+1) 是二次函数,则m的值为 .?
解:∵二次函数的自变量x的最高指数是2,
∴m2-6m-5=2,由二次项系数不为0,得m+1≠0,
解得m=7.
提示:二次项系数不为0.
二次函数的概念
练一练:下列函数表达式中,一定为二次函数的是( )
A.y=3x-1
B.y=ax2+bx+c
C.s=2t2-2t+1
D.
C
二次函数的概念
归纳:1.在二次函数y=ax2+bx+c中,必须注意限制条件a≠0.
2.任何一个二次函数都可以化成y=ax2+bx+c(a,b,c为常数,且a≠0)的形式,因此把y=ax2+bx+c(a,b,c为常数,且a≠0)叫做二次函数的一般式.
3.当a≠0时,y=ax2+bx+c才是二次函数.当a=0时,y=bx+c,若b≠0,则它是一次函数,若b=0,则y=c是一个常数函数.
4.在y=ax2+bx+c(a≠0)中,x的取值范围是全体实数.
列二次函数表达式
问题1 新学期开学,全班同学见面时相互亲切握手问候.设全班有m名同学,每两人之间都握手一次,用y表示全班同学握手的总次数.
(1)请用含m的代数式表示y,说明y是m的二次函数,指出该函数中对应的a,b,c的值.
(2)若全班有45名同学,则这样握手的总次数是多少?
解:(1) .因为m的最高次数是2,所以y是m的二次函数,对应的a,b,c的值依次为
(2)当m=45时, .
列二次函数表达式
归纳:根据实际问题列二次函数的表达式应注意:
(1)正确辨别自变量与因变量;
(2)确保找到正确的等量关系;
(3)将列出的关系式整理成y=ax2+bx+c(a≠0)的形式;
(4)确保自变量有意义.
列二次函数表达式
练一练:菱形的两条对角线的和为26 cm,则菱形的面积S(cm2)与其中一条对角线长x(cm)之间的函数关系为___________,是____次函数,自变量x的取值范围是___________.
0<x<26
二
S=-12x2+13x
CONTENTS
3
B
1.下列函数:
①y=2(x-1)(x+4);
②y=3(x-1)2+2;
③y=x2+ +1;
④y=(x-3)2-x2.
其中不是二次函数的是( )
A.①② B.③④
C.①③ D.②④
2.国家决定对某药品价格分两次降价,若设平均每次降价的百分率为x,该药品原价为18元,降价后的价格为y元,则y与x的函数关系式为( )
A.y=36(1-x)
B.y=36(1+x)
C.y=18(1-x)2
D.y=18(1+x)2
C
3.已知二次函数y=1-2x-x2,其中二次项系数a=_____,一次项系数b=_____,常数项c=_____.
4.对于二次函数y=x2+3x-2,当x=-1时,y的值为_____,当y=8时,x的值为_____.
1
-1
-2
2或-5
-4
5.已知函数y=(m+3)xm2+2m-1,当m为何值时,y是x的二次函数?
故当m=1时,y是x的二次函数.
解: 依题意,得
m+3≠0,
m2+2m-1=2,
m=1.
解得
6.某水果批发商销售每箱进价为40元的苹果,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售价x(元/箱)之间的函数关系式;
解: y=-3x+240.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.(不必写出x的取值范围)
=-3x2+360x-9600.
解: w=y·(x-40)
=(-3x+240)(x-40)
CONTENTS
4
二次函数
定 义
一般形式
一般地,函数y=ax2+bx+c(a,b,c是常数,且a≠0),叫做二次函数.
y=ax?+bx+c(a,b,c是常数,a≠ 0),ax?是二次项,a是二次项系数,bx是一次项,b是一次项系数,c是常数项
特点
函数表达式是整式
自变量的最高次数是2
二次项系数不等于零
列二次函数表达式(注意自变量的取值范围)
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
30.1 二次函数
1
2
3
CONTENTS
1
想一想:
.
以点O为圆心画圆 ,
改变半径r,圆有哪些改变?
O
CONTENTS
2
二次函数的概念
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
(1)设红色瓷砖的总数为y块.
①用含n的代数式表示y,
则y= .?
②y与n具有怎样的函数关系?
4n+6
一次函数
二次函数的概念
(2)设白色瓷砖的总数为z块.
①用含n的代数式表示z,
则z= .?
②z是n的函数吗?说说理由.
z是n的函数
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
n2+n-6
二次函数的概念
问题2 某企业今年第一季度的产值为80万元,预计产值的季平均增长率为x.
分析:
(1)设第二季度的产值为y万元,则y= .
设第三季度的产值为z万元,则z= .?
(2)y,z都是x的函数吗?它们的表达式有什么不同?
y=80x+80
z=80x2+160x+80
y=80x+80,一次函数.
z=80x2+160x+80,z是x的函数.
二次函数的概念
问题3 观察下面两个函数:z=n2+n-6,z=80x2+160x+80,
(1)这两个函数与我们学过的函数有什么不同?
(2)这两个函数的自变量x的最高指数分别是多少?
(3)你能说出函数表达式右边的二次项,一次项,常数项及二次项系数,一次项系数吗?
(4)通过观察,你能归纳出这种函数的一般形式吗?
二次函数的概念
定义:一般地,如果两个变量x和y之间的函数关系可以表示成y=ax2+bx+c(a,b,c是常数,且a≠0),那么称y为x的二次函数.其中,a叫做二次项系数,b叫做一次项系数,c叫做常数项.
二次函数的概念
想一想:(1)二次项系数能不能为0?一次项系数和常数项呢?为什么?
(2)如何判断一个函数是不是二次函数?
(3)二次函数的一般形式与一元二次方程的一般形式有什么关系?
(4)函数 是不是二次函数?
(1)函数表达式的右边是整式形式;
(2)自变量的最高指数是2;
(3)二次项系数不为0.
二次函数的概念
想一想:1.请分别指出 的二次项系数、一次项系数和常数项.
2.谈谈一次函数、反比例函数、二次函数有什么不同.
二次函数的概念
例 若y=(m+1) 是二次函数,则m的值为 .?
解:∵二次函数的自变量x的最高指数是2,
∴m2-6m-5=2,由二次项系数不为0,得m+1≠0,
解得m=7.
提示:二次项系数不为0.
二次函数的概念
练一练:下列函数表达式中,一定为二次函数的是( )
A.y=3x-1
B.y=ax2+bx+c
C.s=2t2-2t+1
D.
C
二次函数的概念
归纳:1.在二次函数y=ax2+bx+c中,必须注意限制条件a≠0.
2.任何一个二次函数都可以化成y=ax2+bx+c(a,b,c为常数,且a≠0)的形式,因此把y=ax2+bx+c(a,b,c为常数,且a≠0)叫做二次函数的一般式.
3.当a≠0时,y=ax2+bx+c才是二次函数.当a=0时,y=bx+c,若b≠0,则它是一次函数,若b=0,则y=c是一个常数函数.
4.在y=ax2+bx+c(a≠0)中,x的取值范围是全体实数.
列二次函数表达式
问题1 新学期开学,全班同学见面时相互亲切握手问候.设全班有m名同学,每两人之间都握手一次,用y表示全班同学握手的总次数.
(1)请用含m的代数式表示y,说明y是m的二次函数,指出该函数中对应的a,b,c的值.
(2)若全班有45名同学,则这样握手的总次数是多少?
解:(1) .因为m的最高次数是2,所以y是m的二次函数,对应的a,b,c的值依次为
(2)当m=45时, .
列二次函数表达式
归纳:根据实际问题列二次函数的表达式应注意:
(1)正确辨别自变量与因变量;
(2)确保找到正确的等量关系;
(3)将列出的关系式整理成y=ax2+bx+c(a≠0)的形式;
(4)确保自变量有意义.
列二次函数表达式
练一练:菱形的两条对角线的和为26 cm,则菱形的面积S(cm2)与其中一条对角线长x(cm)之间的函数关系为___________,是____次函数,自变量x的取值范围是___________.
0<x<26
二
S=-12x2+13x
CONTENTS
3
B
1.下列函数:
①y=2(x-1)(x+4);
②y=3(x-1)2+2;
③y=x2+ +1;
④y=(x-3)2-x2.
其中不是二次函数的是( )
A.①② B.③④
C.①③ D.②④
2.国家决定对某药品价格分两次降价,若设平均每次降价的百分率为x,该药品原价为18元,降价后的价格为y元,则y与x的函数关系式为( )
A.y=36(1-x)
B.y=36(1+x)
C.y=18(1-x)2
D.y=18(1+x)2
C
3.已知二次函数y=1-2x-x2,其中二次项系数a=_____,一次项系数b=_____,常数项c=_____.
4.对于二次函数y=x2+3x-2,当x=-1时,y的值为_____,当y=8时,x的值为_____.
1
-1
-2
2或-5
-4
5.已知函数y=(m+3)xm2+2m-1,当m为何值时,y是x的二次函数?
故当m=1时,y是x的二次函数.
解: 依题意,得
m+3≠0,
m2+2m-1=2,
m=1.
解得
6.某水果批发商销售每箱进价为40元的苹果,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售价x(元/箱)之间的函数关系式;
解: y=-3x+240.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.(不必写出x的取值范围)
=-3x2+360x-9600.
解: w=y·(x-40)
=(-3x+240)(x-40)
CONTENTS
4
二次函数
定 义
一般形式
一般地,函数y=ax2+bx+c(a,b,c是常数,且a≠0),叫做二次函数.
y=ax?+bx+c(a,b,c是常数,a≠ 0),ax?是二次项,a是二次项系数,bx是一次项,b是一次项系数,c是常数项
特点
函数表达式是整式
自变量的最高次数是2
二次项系数不等于零
列二次函数表达式(注意自变量的取值范围)
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
