高中物理人教版必修2全册综合卷 Word版含解析
文档属性
| 名称 | 高中物理人教版必修2全册综合卷 Word版含解析 |

|
|
| 格式 | DOC | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-18 00:00:00 | ||
图片预览



文档简介
一、单项选择题(共6小题,每小题4分)
1.有一条两岸平直、河水均匀流动、流速恒为v的大河.小明驾着小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直.去程与回程所用时间的比值为k,船在静水中的速度大小相同,则小船在静水中的速度大小为( B )
A. B.
C. D.
解析:去程时船头垂直河岸如图所示,由合运动与分运动具有等时性并设河宽为d,则去程时间t1=;回程时行驶路线垂直河岸,故回程时间t2=,由题意有=k,则k=,得v1==,选项B正确.
2.如图所示,自动卸货车静止在水平地面上,车厢在液压机的作用下,θ角缓慢增大,在货物相对车厢仍然静止的过程中,下列说法正确的是( A )
A.货物受到的支持力变小
B.货物受到的摩擦力变小
C.货物受到的支持力对货物做负功
D.货物受到的摩擦力对货物做负功
解析:货物处于平衡状态,受到重力mg、支持力FN和摩擦力Ff,则根据平衡条件有:mgsinθ=Ff,FN=mgcosθ,当θ增大 时,Ff增大,FN减小,故A正确,B错误.货物受到的支持力的方向与瞬时速度方向相同,所以支持力对货物做正功,故C错误;摩擦力的方向与位移方向垂直,不做功,故D错误.
3.假设在质量与地球质量相同、半径为地球半径两倍的某天体上进行运动比赛,那么与地球上的比赛成绩相比,下列说法正确的是( A )
①跳高运动员的成绩会更好
②用弹簧秤称体重时,体重数值会变得更小
③投掷铁饼的距离会更远
④用手投出的篮球,水平方向的分速度会更大
A.①②③ B.②③④
C.①③④ D.①②④
解析:根据万有引力定律可知人在该天体上受到的引力小于地球上的重力,即物体好像变“轻”了,所以①、②、③是正确的,选A.
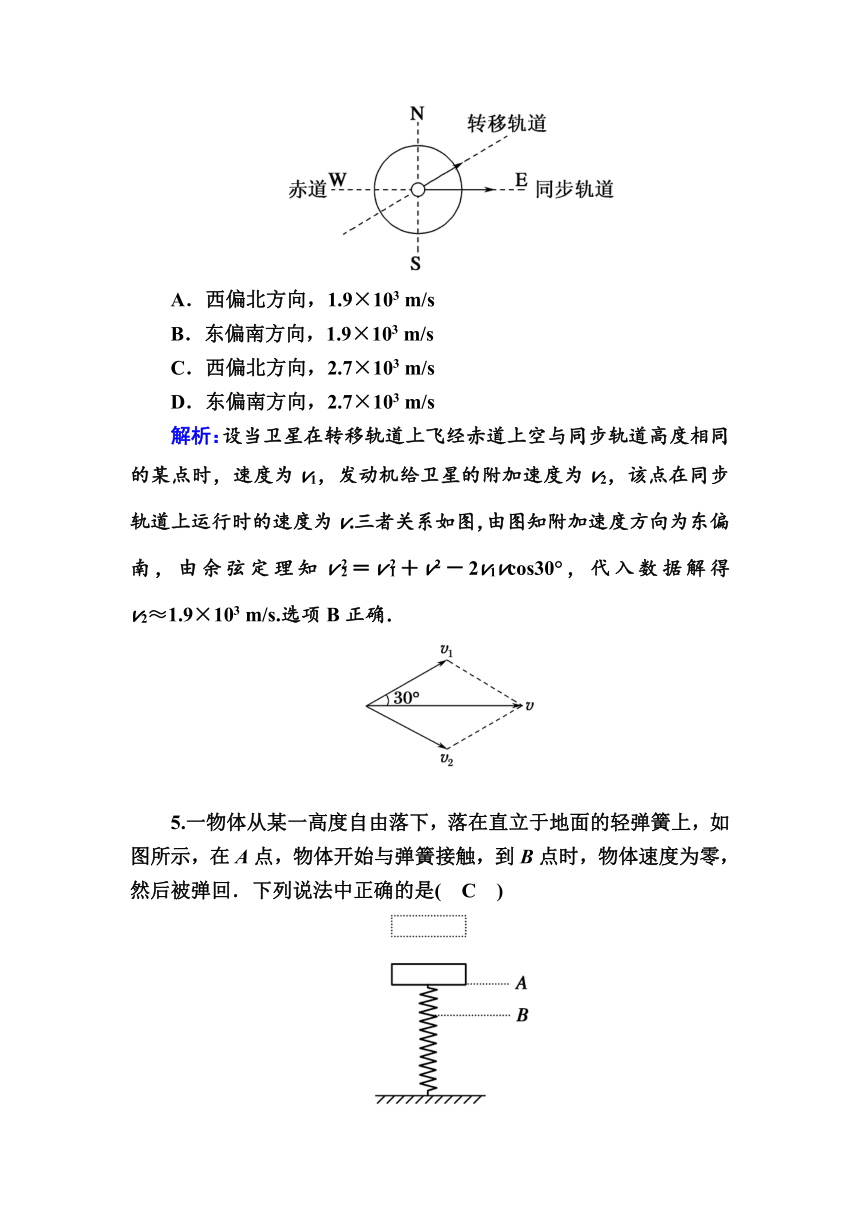
4.由于卫星的发射场不在赤道上,同步卫星发射后需要从转移轨道经过调整再进入地球同步轨道.当卫星在转移轨道上飞经赤道上空时,发动机点火,给卫星一附加速度,使卫星沿同步轨道运行.已知同步卫星的环绕速度约为3.1×103 m/s,某次发射卫星飞经赤道上空时的速度为1.55×103 m/s,此时卫星的高度与同步轨道的高度相同,转移轨道和同步轨道的夹角为30°,如图所示,发动机给卫星的附加速度的方向和大小约为( B )
A.西偏北方向,1.9×103 m/s
B.东偏南方向,1.9×103 m/s
C.西偏北方向,2.7×103 m/s
D.东偏南方向,2.7×103 m/s
解析:设当卫星在转移轨道上飞经赤道上空与同步轨道高度相同的某点时,速度为v1,发动机给卫星的附加速度为v2,该点在同步轨道上运行时的速度为v.三者关系如图,由图知附加速度方向为东偏南,由余弦定理知v=v+v2-2v1vcos30°,代入数据解得v2≈1.9×103 m/s.选项B正确.
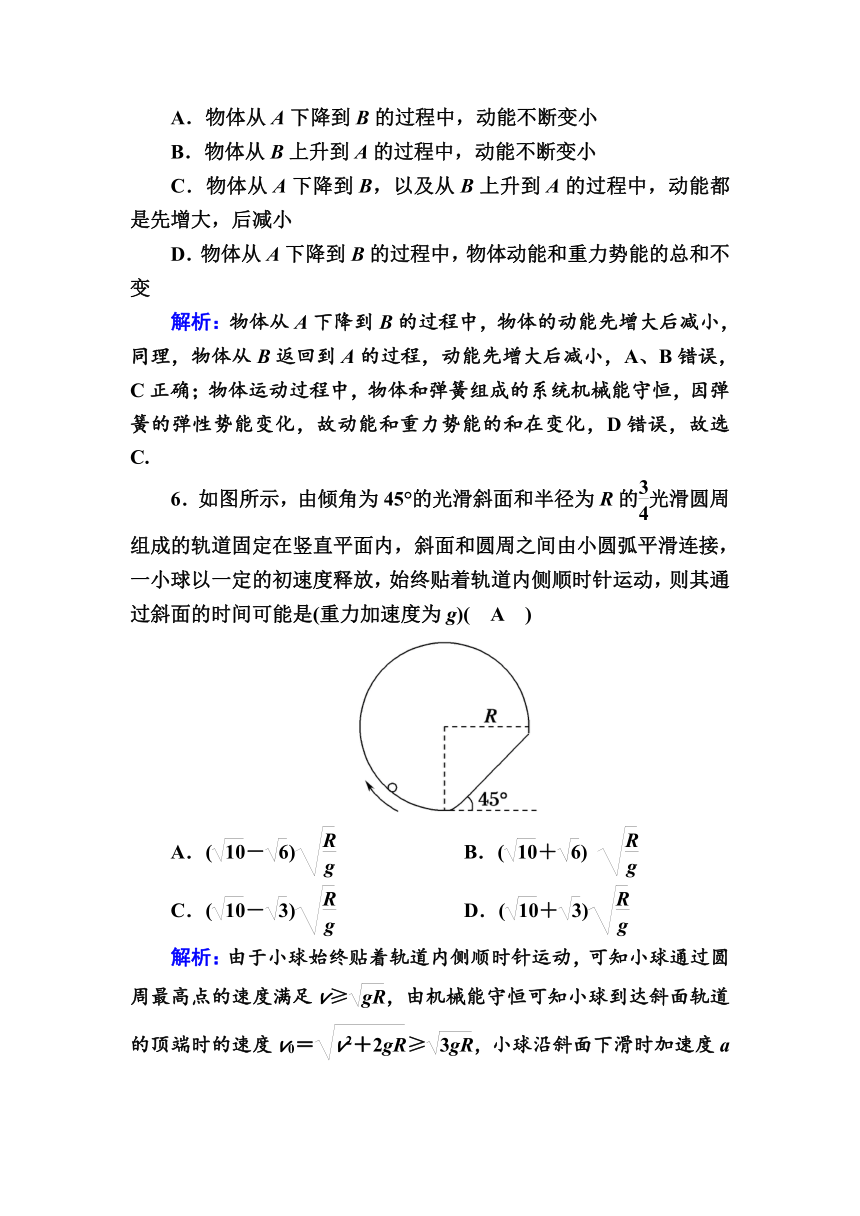
5.一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示,在A点,物体开始与弹簧接触,到B点时,物体速度为零,然后被弹回.下列说法中正确的是( C )
A.物体从A下降到B的过程中,动能不断变小
B.物体从B上升到A的过程中,动能不断变小
C.物体从A下降到B,以及从B上升到A的过程中,动能都是先增大,后减小
D.物体从A下降到B的过程中,物体动能和重力势能的总和不变
解析:物体从A下降到B的过程中,物体的动能先增大后减小,同理,物体从B返回到A的过程,动能先增大后减小,A、B错误,C正确;物体运动过程中,物体和弹簧组成的系统机械能守恒,因弹簧的弹性势能变化,故动能和重力势能的和在变化,D错误,故选C.
6.如图所示,由倾角为45°的光滑斜面和半径为R的光滑圆周组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接,一小球以一定的初速度释放,始终贴着轨道内侧顺时针运动,则其通过斜面的时间可能是(重力加速度为g)( A )
A.(-) B.(+)
C.(-) D.(+)
解析:由于小球始终贴着轨道内侧顺时针运动,可知小球通过圆周最高点的速度满足v≥,由机械能守恒可知小球到达斜面轨道的顶端时的速度v0=≥,小球沿斜面下滑时加速度a=gsin45°=g,则由运动学公式有R=v0t+at2可解得0二、多项选择题(共4小题,每小题4分)
7.如图a所示,甲、乙两个小球可视为质点,甲球沿倾角为30°的光滑长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图b所示.下列说法正确的是( BC )
A.甲球机械能不守恒,乙球机械能守恒
B.甲、乙两球的质量之比为4?1
C.甲、乙两球的动能相等时,两球重力的瞬时功率之比为1?1
D.甲、乙两球的动能相等时,两球高度相同
解析:甲、乙两球在运动的过程中都是只有重力做功,所以甲、乙两球机械能都守恒,故A错误;根据动能定理F合x=ΔEk,可知动能与位移的图象斜率表示合外力大小,甲球的合外力为m甲gsin30°,乙球的合外力为m乙g,由题图知m甲gsin30°=2m乙g,所以m甲?m乙=4?1,故B正确;根据Ek=mv2知,动能相等时,=,两球重力的瞬时功率之比=,所以C正确;由题图知,甲、乙两球的动能均为Ek0时,两球高度不相同,所以D错误.
8.2016年9月落成起用的“中国天眼”是我国自主研制的、世界最大最灵敏的单口径射电望远镜,如图所示.射电望远镜是观测和研究来自天体的射电波的基本设备,脉冲星、宇宙微波背景辐射等天文学的重大发现都与射电望远镜有关.脉冲星是一种高速自转的中子星,它的密度极高,每立方厘米质量达上亿吨.脉冲星在计时、引力波探测、广义相对论检验等领域具有重要应用.到目前为止,“中国天眼”已探测到数十个优质脉冲星候选体.其中脉冲星FP1的自转周期为1.83 s,距离地球约1.6万光年;脉冲星FP2的自转周期为0.59 s,距离地球约4 100光年.根据以上资料可以判断,下列说法中正确的是( AD )
A.脉冲星FP1的自转周期小于地球的自转周期
B.脉冲星FP1到地球的距离小于太阳到地球的距离
C.脉冲星FP1的自转角速度大于脉冲星FP2的自转角速度
D.脉冲星FP1的自转角速度小于脉冲星FP2的自转角速度
解析:脉冲星FP1的自转周期为1.83 s,地球自转周期为1天,显然脉冲星FP1的自转周期小于地球的自转周期,故A正确;脉冲星FP1到地球的距离约1.6万光年,即光1.6万年通过的路程,而光从太阳到地球只要8分钟多点,故脉冲星FP1到地球的距离大于太阳到地球的距离,故B错误;脉冲星FP1的自转周期为1.83 s,脉冲星FP2的自转周期为0.59 s,根据ω=,脉冲星FP1的自转角速度小于脉冲星FP2的自转角速度,故C错误,D正确;故选A、D.
9.质量为m的物体始终静止在倾角为θ的斜面上,下列说法正确的是( ABC )
A.若斜面水平向右匀速运动距离x,斜面对物体不做功
B.若斜面向上匀速运动距离x,斜面对物体做功mgx
C.若斜面水平向左以加速度a运动距离x,斜面对物体做功max
D.若斜面向下以加速度a运动距离x,斜面对物体做功m(g+a)x
解析:物体受到平衡力作用而处于匀速直线运动状态,与重力相平衡的力是斜面给它的作用力,方向竖直向上.斜面沿水平方向匀速运动时,力与位移垂直,斜面对物体不做功.斜面向上匀速运动时,力与位移同向,W=F·x=mgx.斜面水平向左加速运动时,物体所受的合外力为ma,恰等于斜面给它的作用力在位移方向的分量,W=F·x=max.斜面向下加速时,对物体有mg+F=ma,W=F·x=m(a-g)·x,故选A、B、C.
10.如图所示,M为固定在桌面上的异形木块,abcd为圆周的光滑轨道,a为轨道最高点,de面水平且与圆心等高.今将质量为m的小球在d点的正上方高为h处由静止释放,使其自由下落到d处后,又切入圆轨道运动,则下列说法正确的是( CD )
A.在h一定的条件下,释放后小球的运动情况与小球的质量有关
B.只要改变h的大小,就能使小球在通过a点之后既可能落回轨道之内,又可能落到de面上
C.无论怎样改变h的大小,都不可能使小球在通过a点之后,又落回轨道之内
D.要使小球飞出de面之外(即落在e的右边)是可能的
解析:只要小球能通过轨道的最高点a,即有va≥.小球能否落回轨道之内,取决于小球离开a点后做平抛运动的水平射程x,由平抛运动公式x=vat及R=gt2得x≥R,由此可知,小球在通过a点之后,不可能落回轨道之内,但可能飞出de面之外,C、D正确.
三、填空题(共2小题,共14分)
11.(6分)我国已启动了月球探测计划——“嫦娥工程”.右图所示为“嫦娥一号”月球探测器飞行路线的示意图.
(1)在探测器飞离地球的过程中,地球对它的引力逐渐减小(填“增大”“减小”或“不变”).
(2)已知月球与地球的质量之比为M月?M地=1?81,当探测器飞至月地连线上某点P时,月球与地球对它的引力恰好相等,此时P点到月心与到地心的距离之比为1?9.
(3)结合图中信息,通过推理,可以得出的结论是BD.
A.探测器飞离地球时速度方向指向月球
B.探测器经过多次轨道修正,进入预定绕月轨道
C.探测器绕地球的旋转方向与绕月球的旋转方向一致
D.探测器进入绕月轨道后,运行半径逐渐减小,直至到达预定轨道
解析:(1)根据万有引力定律F=G可知,当距离增大时,引力减小.
(2)根据万有引力定律及题意得G=G
又M月?M地=1?81,所以r月?r地=1?9.
(3)由探测器的飞行路线可以看出:探测器飞离地球时速度方向指向月球公转的前方,当到达月球轨道时与月球“相遇”,选项A错误;探测器经过多次轨道修正后,才进入预定绕月轨道,选项B正确;探测器绕地球的旋转方向为逆时针方向,绕月球的旋转方向为顺时针方向,选项C错误;探测器进入绕月轨道后,运行半径逐渐减小,直至到达预定轨道,选项D正确.
12.(8分)探究能力是进行物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系,某同学采用了下述实验方法进行探索:如图所示,先让砂轮由动力带动匀速旋转,测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据,得出结论.经实验测得的几组ω和n如下表所示:
ω/(rad·s-1) 0.5 1 2 3 4
n 5 20 80 180 320
Ek/J 0.5 2 8 18 32
另外已测得砂轮转轴的直径为1 cm,转轴间的摩擦力为 N.
(1)计算出砂轮每次脱离动力的转动动能,并填入上表中.
(2)由上述数据推导出该砂轮的转动动能Ek与角速度ω的关系式为Ek=2ω2.
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s,则它转过45圈后的角速度为2 rad/s.
解析:(1)从脱离动力到最后停止转动,由动能定理得
-Ff·n·πD=0-Ek0,即Ek0=nFfπD=0.1n.
将n的不同数值代入可得到相应的转动动能如下表:
Ek/J 0.5 2 8 18 32
(2)观察数据特点可以归纳出该砂轮的转动动能Ek与角速度ω的关系式为:Ek=2ω2.
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s,则此时砂轮脱离时的动能Ek0=2ω2=12.5 J,转过45圈时的动能:Ek=2ω′2,此过程摩擦力做功W=-f·n·πD=-4.5 J,再根据动能定理得:W=Ek-Ek0,代入数据得:ω′=2 rad/s.
四、计算题(共4小题,共46分)
13.(8分)汽车在平直的公路上由静止启动,做直线运动,下图中曲线1表示汽车运动的速度和时间的关系(除6~16 s时间段图线为曲线外,其余时间段图线均为直线),直线2表示汽车的功率和时间的关系.设汽车在运动过程中受到的阻力不变,在16 s末汽车的速度恰好达到最大.
(1)定性描述汽车的运动状态;
(2)求汽车受到的阻力和最大牵引力;
(3)求汽车的质量.
解析:(1)汽车刚开始做初速度为零的匀加速直线运动,6 s末开始做加速度减小的变加速直线运动,16 s末开始做匀速直线运动.
(2)汽车受到的阻力f== N≈583.3 N.
6 s末的速度为8 m/s,是匀加速直线运动的末速度,此时牵引力最大,F== N=875 N.
(3)汽车匀加速运动的加速度为a= m/s2= m/s2
由牛顿第二定律得F-f=ma
解得m== kg≈218.8 kg.
答案:(1)见解析 (2)583.3 N 875 N (3)218.8 kg
14.(12分)某一空间飞行器质量为m,从地面起飞时,恰好沿与水平方向成θ=30°角的直线斜向右上方匀加速飞行,此时,发动机提供的动力方向与水平方向夹角α=60°,经时间t后,将动力方向沿逆时针旋转60°,同时适当调节其大小,使飞行器沿原方向匀减速飞行,飞行器所受空气阻力不计,重力加速度为g,求:
(1)t时刻飞行器的速度;
(2)t时刻发动机动力的功率;
(3)从起飞到上升到最大高度的整个过程中,飞行器发动机动力做的总功.
解析:(1)对飞行器进行受力分析如图,则
Fsinα-mg=may①
Fcosα=max②
又=tanθ③
联立①②③式,并代入数据得F=mg.
飞行器的加速度a=.
联立以上各式,并代入数据得a=g.
t时刻飞行器的速度v=at=gt.
(2)设t时刻发动机动力的功率为P,则
P=Fvcos30°=mg2t.
(3)飞行器加速过程位移为x1=at2.
飞行器加速过程,由动能定理得
W1-mgx1sin30°=mv2.
将动力方向沿逆时针旋转60°后与速度方向垂直,所以减速过程发动机动力做的功W2=0.
飞行器从地面到最大高度的整个过程中发动机动力做的功W=W1+W2.
联立上式得W=mg2t2.
答案:(1)gt (2)mg2t (3)mg2t2
15.(12分)一组太空人乘坐太空穿梭机,去修理距离地球表面6.0×105 m的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数千米处.如图所示,设G为引力常量,M为地球质量(已知地球半径R=6.4×106 m,地球表面重力加速度g=9.8 m/s2,地球的第一宇宙速度v=7.9 km/s).
(1)在穿梭机内,一质量为70 kg的太空人的视重是多少?
(2)计算轨道上的重力加速度及穿梭机在轨道上的速率和周期.
解析:(1)穿梭机内的人处于完全失重状态,故视重为0.
(2)由mg=G,得g=,g′=,则==≈0.84,所以轨道上的重力加速度g′=0.84g=0.84×9.8 m/s2≈8.2 m/s2;
由G=m,得v=,
则v′=,得==
≈0.96.
所以穿梭机在轨道上的速率
v′=0.96v=0.96×7.9 km/s≈7.6 km/s;
由v=得穿梭机在轨道上的周期
T= s≈5.8×103 s.
答案:(1)0 (2)8.2 m/s2 7.6 km/s 5.8×103 s
16.(14分)如图所示,小球P用长l=1 m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2π rad/s.另一小球Q质量m=1 kg,在高出水平面h=0.8 m的水平槽上.槽与绳平行,且槽光滑,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,两小球同时开始运动.当小球Q运动到A点时,撤去力F.求:
(1)恒力F为何值时两小球可能相碰?
(2)在满足(1)条件的前提下,小球Q运动到槽口的最短时间和相应的小球Q在槽上滑行的距离.(g取10 m/s2)
解析:(1)设小球Q在水平槽上的运动时间为t1,则到达A点时的速度v0=t1①
小球Q做平抛运动时,有h=gt②
l1=v0t2③
由②得平抛运动的时间t2==0.4 s.
要使两小球相碰,小球Q做平抛运动的水平位移
l1=l=1 m.
由③得初速度v0== m/s=2.5 m/s.
根据题中给出的条件可知两球相遇的时间关系为t2+t1=+nT,其中T==1 s,则t1=T-t2=(n+0.1) s (n=0,1,2,…)
由①得恒力F== N(n=0,1,2,…).
(2)当n=0时,小球Q运动到槽口的时间最短
最短时间tmin=-t2=0.1 s
相应时间内小球Q在槽上滑行的距离
x=tmin=0.125 m.
答案:(1) N(n=0,1,2,…) (2)0.1 s 0.125 m
1.有一条两岸平直、河水均匀流动、流速恒为v的大河.小明驾着小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直.去程与回程所用时间的比值为k,船在静水中的速度大小相同,则小船在静水中的速度大小为( B )
A. B.
C. D.
解析:去程时船头垂直河岸如图所示,由合运动与分运动具有等时性并设河宽为d,则去程时间t1=;回程时行驶路线垂直河岸,故回程时间t2=,由题意有=k,则k=,得v1==,选项B正确.
2.如图所示,自动卸货车静止在水平地面上,车厢在液压机的作用下,θ角缓慢增大,在货物相对车厢仍然静止的过程中,下列说法正确的是( A )
A.货物受到的支持力变小
B.货物受到的摩擦力变小
C.货物受到的支持力对货物做负功
D.货物受到的摩擦力对货物做负功
解析:货物处于平衡状态,受到重力mg、支持力FN和摩擦力Ff,则根据平衡条件有:mgsinθ=Ff,FN=mgcosθ,当θ增大 时,Ff增大,FN减小,故A正确,B错误.货物受到的支持力的方向与瞬时速度方向相同,所以支持力对货物做正功,故C错误;摩擦力的方向与位移方向垂直,不做功,故D错误.
3.假设在质量与地球质量相同、半径为地球半径两倍的某天体上进行运动比赛,那么与地球上的比赛成绩相比,下列说法正确的是( A )
①跳高运动员的成绩会更好
②用弹簧秤称体重时,体重数值会变得更小
③投掷铁饼的距离会更远
④用手投出的篮球,水平方向的分速度会更大
A.①②③ B.②③④
C.①③④ D.①②④
解析:根据万有引力定律可知人在该天体上受到的引力小于地球上的重力,即物体好像变“轻”了,所以①、②、③是正确的,选A.
4.由于卫星的发射场不在赤道上,同步卫星发射后需要从转移轨道经过调整再进入地球同步轨道.当卫星在转移轨道上飞经赤道上空时,发动机点火,给卫星一附加速度,使卫星沿同步轨道运行.已知同步卫星的环绕速度约为3.1×103 m/s,某次发射卫星飞经赤道上空时的速度为1.55×103 m/s,此时卫星的高度与同步轨道的高度相同,转移轨道和同步轨道的夹角为30°,如图所示,发动机给卫星的附加速度的方向和大小约为( B )
A.西偏北方向,1.9×103 m/s
B.东偏南方向,1.9×103 m/s
C.西偏北方向,2.7×103 m/s
D.东偏南方向,2.7×103 m/s
解析:设当卫星在转移轨道上飞经赤道上空与同步轨道高度相同的某点时,速度为v1,发动机给卫星的附加速度为v2,该点在同步轨道上运行时的速度为v.三者关系如图,由图知附加速度方向为东偏南,由余弦定理知v=v+v2-2v1vcos30°,代入数据解得v2≈1.9×103 m/s.选项B正确.
5.一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示,在A点,物体开始与弹簧接触,到B点时,物体速度为零,然后被弹回.下列说法中正确的是( C )
A.物体从A下降到B的过程中,动能不断变小
B.物体从B上升到A的过程中,动能不断变小
C.物体从A下降到B,以及从B上升到A的过程中,动能都是先增大,后减小
D.物体从A下降到B的过程中,物体动能和重力势能的总和不变
解析:物体从A下降到B的过程中,物体的动能先增大后减小,同理,物体从B返回到A的过程,动能先增大后减小,A、B错误,C正确;物体运动过程中,物体和弹簧组成的系统机械能守恒,因弹簧的弹性势能变化,故动能和重力势能的和在变化,D错误,故选C.
6.如图所示,由倾角为45°的光滑斜面和半径为R的光滑圆周组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接,一小球以一定的初速度释放,始终贴着轨道内侧顺时针运动,则其通过斜面的时间可能是(重力加速度为g)( A )
A.(-) B.(+)
C.(-) D.(+)
解析:由于小球始终贴着轨道内侧顺时针运动,可知小球通过圆周最高点的速度满足v≥,由机械能守恒可知小球到达斜面轨道的顶端时的速度v0=≥,小球沿斜面下滑时加速度a=gsin45°=g,则由运动学公式有R=v0t+at2可解得0
7.如图a所示,甲、乙两个小球可视为质点,甲球沿倾角为30°的光滑长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图b所示.下列说法正确的是( BC )
A.甲球机械能不守恒,乙球机械能守恒
B.甲、乙两球的质量之比为4?1
C.甲、乙两球的动能相等时,两球重力的瞬时功率之比为1?1
D.甲、乙两球的动能相等时,两球高度相同
解析:甲、乙两球在运动的过程中都是只有重力做功,所以甲、乙两球机械能都守恒,故A错误;根据动能定理F合x=ΔEk,可知动能与位移的图象斜率表示合外力大小,甲球的合外力为m甲gsin30°,乙球的合外力为m乙g,由题图知m甲gsin30°=2m乙g,所以m甲?m乙=4?1,故B正确;根据Ek=mv2知,动能相等时,=,两球重力的瞬时功率之比=,所以C正确;由题图知,甲、乙两球的动能均为Ek0时,两球高度不相同,所以D错误.
8.2016年9月落成起用的“中国天眼”是我国自主研制的、世界最大最灵敏的单口径射电望远镜,如图所示.射电望远镜是观测和研究来自天体的射电波的基本设备,脉冲星、宇宙微波背景辐射等天文学的重大发现都与射电望远镜有关.脉冲星是一种高速自转的中子星,它的密度极高,每立方厘米质量达上亿吨.脉冲星在计时、引力波探测、广义相对论检验等领域具有重要应用.到目前为止,“中国天眼”已探测到数十个优质脉冲星候选体.其中脉冲星FP1的自转周期为1.83 s,距离地球约1.6万光年;脉冲星FP2的自转周期为0.59 s,距离地球约4 100光年.根据以上资料可以判断,下列说法中正确的是( AD )
A.脉冲星FP1的自转周期小于地球的自转周期
B.脉冲星FP1到地球的距离小于太阳到地球的距离
C.脉冲星FP1的自转角速度大于脉冲星FP2的自转角速度
D.脉冲星FP1的自转角速度小于脉冲星FP2的自转角速度
解析:脉冲星FP1的自转周期为1.83 s,地球自转周期为1天,显然脉冲星FP1的自转周期小于地球的自转周期,故A正确;脉冲星FP1到地球的距离约1.6万光年,即光1.6万年通过的路程,而光从太阳到地球只要8分钟多点,故脉冲星FP1到地球的距离大于太阳到地球的距离,故B错误;脉冲星FP1的自转周期为1.83 s,脉冲星FP2的自转周期为0.59 s,根据ω=,脉冲星FP1的自转角速度小于脉冲星FP2的自转角速度,故C错误,D正确;故选A、D.
9.质量为m的物体始终静止在倾角为θ的斜面上,下列说法正确的是( ABC )
A.若斜面水平向右匀速运动距离x,斜面对物体不做功
B.若斜面向上匀速运动距离x,斜面对物体做功mgx
C.若斜面水平向左以加速度a运动距离x,斜面对物体做功max
D.若斜面向下以加速度a运动距离x,斜面对物体做功m(g+a)x
解析:物体受到平衡力作用而处于匀速直线运动状态,与重力相平衡的力是斜面给它的作用力,方向竖直向上.斜面沿水平方向匀速运动时,力与位移垂直,斜面对物体不做功.斜面向上匀速运动时,力与位移同向,W=F·x=mgx.斜面水平向左加速运动时,物体所受的合外力为ma,恰等于斜面给它的作用力在位移方向的分量,W=F·x=max.斜面向下加速时,对物体有mg+F=ma,W=F·x=m(a-g)·x,故选A、B、C.
10.如图所示,M为固定在桌面上的异形木块,abcd为圆周的光滑轨道,a为轨道最高点,de面水平且与圆心等高.今将质量为m的小球在d点的正上方高为h处由静止释放,使其自由下落到d处后,又切入圆轨道运动,则下列说法正确的是( CD )
A.在h一定的条件下,释放后小球的运动情况与小球的质量有关
B.只要改变h的大小,就能使小球在通过a点之后既可能落回轨道之内,又可能落到de面上
C.无论怎样改变h的大小,都不可能使小球在通过a点之后,又落回轨道之内
D.要使小球飞出de面之外(即落在e的右边)是可能的
解析:只要小球能通过轨道的最高点a,即有va≥.小球能否落回轨道之内,取决于小球离开a点后做平抛运动的水平射程x,由平抛运动公式x=vat及R=gt2得x≥R,由此可知,小球在通过a点之后,不可能落回轨道之内,但可能飞出de面之外,C、D正确.
三、填空题(共2小题,共14分)
11.(6分)我国已启动了月球探测计划——“嫦娥工程”.右图所示为“嫦娥一号”月球探测器飞行路线的示意图.
(1)在探测器飞离地球的过程中,地球对它的引力逐渐减小(填“增大”“减小”或“不变”).
(2)已知月球与地球的质量之比为M月?M地=1?81,当探测器飞至月地连线上某点P时,月球与地球对它的引力恰好相等,此时P点到月心与到地心的距离之比为1?9.
(3)结合图中信息,通过推理,可以得出的结论是BD.
A.探测器飞离地球时速度方向指向月球
B.探测器经过多次轨道修正,进入预定绕月轨道
C.探测器绕地球的旋转方向与绕月球的旋转方向一致
D.探测器进入绕月轨道后,运行半径逐渐减小,直至到达预定轨道
解析:(1)根据万有引力定律F=G可知,当距离增大时,引力减小.
(2)根据万有引力定律及题意得G=G
又M月?M地=1?81,所以r月?r地=1?9.
(3)由探测器的飞行路线可以看出:探测器飞离地球时速度方向指向月球公转的前方,当到达月球轨道时与月球“相遇”,选项A错误;探测器经过多次轨道修正后,才进入预定绕月轨道,选项B正确;探测器绕地球的旋转方向为逆时针方向,绕月球的旋转方向为顺时针方向,选项C错误;探测器进入绕月轨道后,运行半径逐渐减小,直至到达预定轨道,选项D正确.
12.(8分)探究能力是进行物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系,某同学采用了下述实验方法进行探索:如图所示,先让砂轮由动力带动匀速旋转,测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据,得出结论.经实验测得的几组ω和n如下表所示:
ω/(rad·s-1) 0.5 1 2 3 4
n 5 20 80 180 320
Ek/J 0.5 2 8 18 32
另外已测得砂轮转轴的直径为1 cm,转轴间的摩擦力为 N.
(1)计算出砂轮每次脱离动力的转动动能,并填入上表中.
(2)由上述数据推导出该砂轮的转动动能Ek与角速度ω的关系式为Ek=2ω2.
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s,则它转过45圈后的角速度为2 rad/s.
解析:(1)从脱离动力到最后停止转动,由动能定理得
-Ff·n·πD=0-Ek0,即Ek0=nFfπD=0.1n.
将n的不同数值代入可得到相应的转动动能如下表:
Ek/J 0.5 2 8 18 32
(2)观察数据特点可以归纳出该砂轮的转动动能Ek与角速度ω的关系式为:Ek=2ω2.
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s,则此时砂轮脱离时的动能Ek0=2ω2=12.5 J,转过45圈时的动能:Ek=2ω′2,此过程摩擦力做功W=-f·n·πD=-4.5 J,再根据动能定理得:W=Ek-Ek0,代入数据得:ω′=2 rad/s.
四、计算题(共4小题,共46分)
13.(8分)汽车在平直的公路上由静止启动,做直线运动,下图中曲线1表示汽车运动的速度和时间的关系(除6~16 s时间段图线为曲线外,其余时间段图线均为直线),直线2表示汽车的功率和时间的关系.设汽车在运动过程中受到的阻力不变,在16 s末汽车的速度恰好达到最大.
(1)定性描述汽车的运动状态;
(2)求汽车受到的阻力和最大牵引力;
(3)求汽车的质量.
解析:(1)汽车刚开始做初速度为零的匀加速直线运动,6 s末开始做加速度减小的变加速直线运动,16 s末开始做匀速直线运动.
(2)汽车受到的阻力f== N≈583.3 N.
6 s末的速度为8 m/s,是匀加速直线运动的末速度,此时牵引力最大,F== N=875 N.
(3)汽车匀加速运动的加速度为a= m/s2= m/s2
由牛顿第二定律得F-f=ma
解得m== kg≈218.8 kg.
答案:(1)见解析 (2)583.3 N 875 N (3)218.8 kg
14.(12分)某一空间飞行器质量为m,从地面起飞时,恰好沿与水平方向成θ=30°角的直线斜向右上方匀加速飞行,此时,发动机提供的动力方向与水平方向夹角α=60°,经时间t后,将动力方向沿逆时针旋转60°,同时适当调节其大小,使飞行器沿原方向匀减速飞行,飞行器所受空气阻力不计,重力加速度为g,求:
(1)t时刻飞行器的速度;
(2)t时刻发动机动力的功率;
(3)从起飞到上升到最大高度的整个过程中,飞行器发动机动力做的总功.
解析:(1)对飞行器进行受力分析如图,则
Fsinα-mg=may①
Fcosα=max②
又=tanθ③
联立①②③式,并代入数据得F=mg.
飞行器的加速度a=.
联立以上各式,并代入数据得a=g.
t时刻飞行器的速度v=at=gt.
(2)设t时刻发动机动力的功率为P,则
P=Fvcos30°=mg2t.
(3)飞行器加速过程位移为x1=at2.
飞行器加速过程,由动能定理得
W1-mgx1sin30°=mv2.
将动力方向沿逆时针旋转60°后与速度方向垂直,所以减速过程发动机动力做的功W2=0.
飞行器从地面到最大高度的整个过程中发动机动力做的功W=W1+W2.
联立上式得W=mg2t2.
答案:(1)gt (2)mg2t (3)mg2t2
15.(12分)一组太空人乘坐太空穿梭机,去修理距离地球表面6.0×105 m的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数千米处.如图所示,设G为引力常量,M为地球质量(已知地球半径R=6.4×106 m,地球表面重力加速度g=9.8 m/s2,地球的第一宇宙速度v=7.9 km/s).
(1)在穿梭机内,一质量为70 kg的太空人的视重是多少?
(2)计算轨道上的重力加速度及穿梭机在轨道上的速率和周期.
解析:(1)穿梭机内的人处于完全失重状态,故视重为0.
(2)由mg=G,得g=,g′=,则==≈0.84,所以轨道上的重力加速度g′=0.84g=0.84×9.8 m/s2≈8.2 m/s2;
由G=m,得v=,
则v′=,得==
≈0.96.
所以穿梭机在轨道上的速率
v′=0.96v=0.96×7.9 km/s≈7.6 km/s;
由v=得穿梭机在轨道上的周期
T= s≈5.8×103 s.
答案:(1)0 (2)8.2 m/s2 7.6 km/s 5.8×103 s
16.(14分)如图所示,小球P用长l=1 m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2π rad/s.另一小球Q质量m=1 kg,在高出水平面h=0.8 m的水平槽上.槽与绳平行,且槽光滑,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,两小球同时开始运动.当小球Q运动到A点时,撤去力F.求:
(1)恒力F为何值时两小球可能相碰?
(2)在满足(1)条件的前提下,小球Q运动到槽口的最短时间和相应的小球Q在槽上滑行的距离.(g取10 m/s2)
解析:(1)设小球Q在水平槽上的运动时间为t1,则到达A点时的速度v0=t1①
小球Q做平抛运动时,有h=gt②
l1=v0t2③
由②得平抛运动的时间t2==0.4 s.
要使两小球相碰,小球Q做平抛运动的水平位移
l1=l=1 m.
由③得初速度v0== m/s=2.5 m/s.
根据题中给出的条件可知两球相遇的时间关系为t2+t1=+nT,其中T==1 s,则t1=T-t2=(n+0.1) s (n=0,1,2,…)
由①得恒力F== N(n=0,1,2,…).
(2)当n=0时,小球Q运动到槽口的时间最短
最短时间tmin=-t2=0.1 s
相应时间内小球Q在槽上滑行的距离
x=tmin=0.125 m.
答案:(1) N(n=0,1,2,…) (2)0.1 s 0.125 m
