人教版A必修1第二章2.1.1 指数与指数幂的运算(41张PPT)
文档属性
| 名称 | 人教版A必修1第二章2.1.1 指数与指数幂的运算(41张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 19:47:49 | ||
图片预览


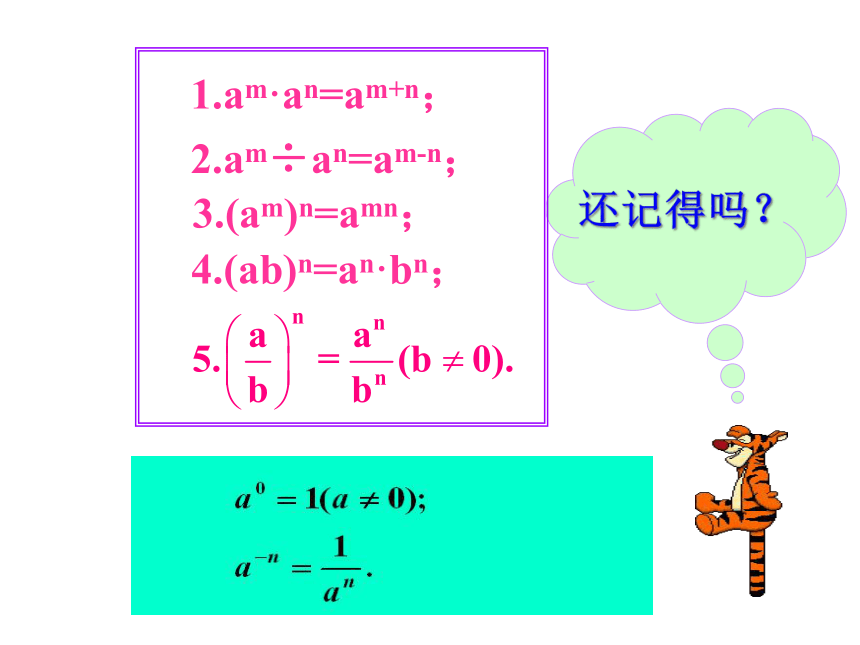








文档简介
n个数(a)的连乘积,用数学式子表示? (n取整数)
初中的知识,可以写出来吗?
新课导入
回顾旧知
正整数指数幂:一个数a的n次幂等于n个a的连乘积,即
an=a·a· ··· ·a
n个
正整数指数幂的运算法则?
还记得吗?
1.am·an=am+n;
2.am÷an=am-n;
3.(am)n=amn;
4.(ab)n=an·bn;
n ∈Z
n ∈N*
前面我们讲的都是正整数指数幂,即n只取正整数,那么n能否取有理数呢?
2.1.1 指数与指数幂的运算
1.在熟练掌握正整数指数幂运算的基础上,理解并掌握分数指数幂、有理数指数幂、无理数指数幂的运算方法与性质.
2.在学习中注意对于不同情况指数幂的运算采取不同的措施,注意偶次方根的两种不同情况.
知识与能力
教学目标
1.通过幂运算律的推广,培养在数学学习过程中能够进行数学推广的能力;
2.培养并体会数形结合的思想,在以后的学习过程中研究函数的能力.
过程与方法
1.经历和体验数学活动的过程以及数学在现实生活中的应用,能够体会一些重要的数学思想.
2.通过课堂学习培养敢于联系实际,勇于发现,大胆探索,合作创新的精神.
情感态度与价值观
掌握并理解分数指数幂、有理数指数幂、无理数指数幂的运算方法与性质.
重点
教学重难点
非整数指数幂意义的了解,特别是对无理数指数幂意义的了解.
难点
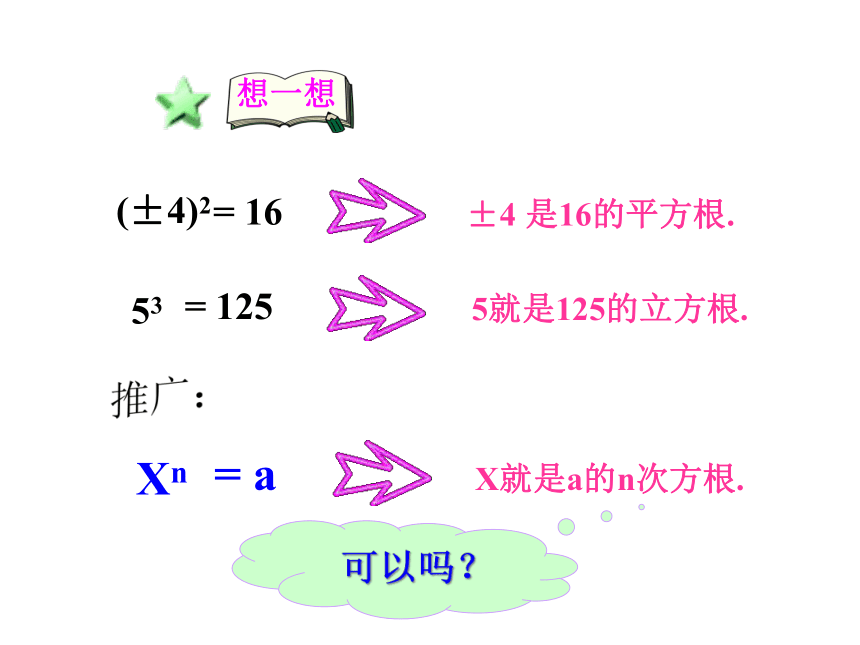
(±4)2
= 16
±4 是16的平方根.
53
= 125
5就是125的立方根.
推广:
Xn
= a
X就是a的n次方根.
可以吗?
想一想
知识要点
根式:
一般地,如xn=a,那么x叫做a的n次方根,其中n>1,且n∈ N* .
根指数
根式
被开方数
认识下
求下列根式值:
小练习
结论?
能得出什么结论吗?
= 3
= -3
=a
=0
=±5
=±2
不存在
=0
结论:
说明
当n是奇数,根式的值是唯一的;
当n是偶数且a>0,根式的值有两个,同时互为相反数;
负数没有偶次方根;
0的任何次方根都是0.
(当n是奇数)
(当n是偶数,且a>0)
探究
表示an的n次方根,等式
= a.
一定成立吗?如果不成立,那么
等于什么?
想一想
探究
=5
= -9
= 25
= 25
= a-b
= b-a
得出什么结论?
结论
想一想
可以这样算吗?
正确吗?
探究
知识要点
正分数指数幂的意义:
探究
(a>0, m、n∈N*,n>1)
结果
想一想
注意
0的正分数指数幂是0, 0的负分数指数幂没有意义。
整数指数幂的运算性质对于有理指数幂也同样适用,即对于任意有理数r,s,均有下面的运算性质:
小练习
求值:
想一想
在前面的学习中,我们已经把指数由
正整数推广到了有理数,那么能不能继续
推广到无理数范围(即实数范围)呢?
推 理
52 = 25 51/2 =
说明
以上结果无需算出,只需了解结果也是一确定实数.
探究
的不足近似值
的近似值
1.4
9.518 269 694
1.41
9.672 669973
1.414
9.735 171 039
1.414 2
9.738 305 174
… …
… …
的过剩近似值
的近似值
1.5
11.180 339 89
1.42
9.829 635 328
1.415
9.750 851 808
1.414 3
9.739 872 62
… …
… …
由上表发现:
的不足近似值从小于 方向逼近 时, 的近似值从小于 的方向逼近 .
同理,当 的过剩近似值从大于 的方向逼近时, 的近似值从大于 的方向逼近 .
常数
知识要点
无理数指数幂:
1.无理数指数幂ax(a>0,x是无理数)是一个确定的实数.
2.有理数指数幂的运算性质同样适用于无理数指数幂.
整数指数幂
有理数指数幂
无理数指数幂
分数指数幂
根式 xn=a
课堂小结
(当n是奇数)
(当n是偶数,
且a>0)
负数没有偶次方根;
0的任何次方根都是0.
实数指数幂的运算法则
1.用根式的形式表示下列各式(a>0)
a1/3 , a3/2 , a-1/2 , a-2/5
解:
随堂练习
2.求下列各式:
解:
3.化简下列各式:
4
=- a-1 .
=xy.
解: (1)原式=(1-a)(a-1)-
4
3
=-(a-1)(a-1)-
4
3
=-(a-1)
4
1
(2)原式=[xy2(xy-1) ] (xy)
2
1
3
1
2
1
=(xy2x y- ) x y
3
1
2
1
2
1
2
1
2
1
=(x y ) x y
2
3
2
3
3
1
2
1
2
1
=x y x y
2
1
2
1
2
1
2
1
(3) (1-a)[(a-1)-2(-a) ] .
2
1
2
1
∴a-1<0.
(3)由(-a) 知 -a≥0,
2
1
∴原式=(1-a)(1-a)-1(-a)
4
1
=(-a) .
4
1
4.计算下列各式:
解:
5.比较
的大小.
解:
6.化简
解:
练习(第54页)
习题答案
初中的知识,可以写出来吗?
新课导入
回顾旧知
正整数指数幂:一个数a的n次幂等于n个a的连乘积,即
an=a·a· ··· ·a
n个
正整数指数幂的运算法则?
还记得吗?
1.am·an=am+n;
2.am÷an=am-n;
3.(am)n=amn;
4.(ab)n=an·bn;
n ∈Z
n ∈N*
前面我们讲的都是正整数指数幂,即n只取正整数,那么n能否取有理数呢?
2.1.1 指数与指数幂的运算
1.在熟练掌握正整数指数幂运算的基础上,理解并掌握分数指数幂、有理数指数幂、无理数指数幂的运算方法与性质.
2.在学习中注意对于不同情况指数幂的运算采取不同的措施,注意偶次方根的两种不同情况.
知识与能力
教学目标
1.通过幂运算律的推广,培养在数学学习过程中能够进行数学推广的能力;
2.培养并体会数形结合的思想,在以后的学习过程中研究函数的能力.
过程与方法
1.经历和体验数学活动的过程以及数学在现实生活中的应用,能够体会一些重要的数学思想.
2.通过课堂学习培养敢于联系实际,勇于发现,大胆探索,合作创新的精神.
情感态度与价值观
掌握并理解分数指数幂、有理数指数幂、无理数指数幂的运算方法与性质.
重点
教学重难点
非整数指数幂意义的了解,特别是对无理数指数幂意义的了解.
难点
(±4)2
= 16
±4 是16的平方根.
53
= 125
5就是125的立方根.
推广:
Xn
= a
X就是a的n次方根.
可以吗?
想一想
知识要点
根式:
一般地,如xn=a,那么x叫做a的n次方根,其中n>1,且n∈ N* .
根指数
根式
被开方数
认识下
求下列根式值:
小练习
结论?
能得出什么结论吗?
= 3
= -3
=a
=0
=±5
=±2
不存在
=0
结论:
说明
当n是奇数,根式的值是唯一的;
当n是偶数且a>0,根式的值有两个,同时互为相反数;
负数没有偶次方根;
0的任何次方根都是0.
(当n是奇数)
(当n是偶数,且a>0)
探究
表示an的n次方根,等式
= a.
一定成立吗?如果不成立,那么
等于什么?
想一想
探究
=5
= -9
= 25
= 25
= a-b
= b-a
得出什么结论?
结论
想一想
可以这样算吗?
正确吗?
探究
知识要点
正分数指数幂的意义:
探究
(a>0, m、n∈N*,n>1)
结果
想一想
注意
0的正分数指数幂是0, 0的负分数指数幂没有意义。
整数指数幂的运算性质对于有理指数幂也同样适用,即对于任意有理数r,s,均有下面的运算性质:
小练习
求值:
想一想
在前面的学习中,我们已经把指数由
正整数推广到了有理数,那么能不能继续
推广到无理数范围(即实数范围)呢?
推 理
52 = 25 51/2 =
说明
以上结果无需算出,只需了解结果也是一确定实数.
探究
的不足近似值
的近似值
1.4
9.518 269 694
1.41
9.672 669973
1.414
9.735 171 039
1.414 2
9.738 305 174
… …
… …
的过剩近似值
的近似值
1.5
11.180 339 89
1.42
9.829 635 328
1.415
9.750 851 808
1.414 3
9.739 872 62
… …
… …
由上表发现:
的不足近似值从小于 方向逼近 时, 的近似值从小于 的方向逼近 .
同理,当 的过剩近似值从大于 的方向逼近时, 的近似值从大于 的方向逼近 .
常数
知识要点
无理数指数幂:
1.无理数指数幂ax(a>0,x是无理数)是一个确定的实数.
2.有理数指数幂的运算性质同样适用于无理数指数幂.
整数指数幂
有理数指数幂
无理数指数幂
分数指数幂
根式 xn=a
课堂小结
(当n是奇数)
(当n是偶数,
且a>0)
负数没有偶次方根;
0的任何次方根都是0.
实数指数幂的运算法则
1.用根式的形式表示下列各式(a>0)
a1/3 , a3/2 , a-1/2 , a-2/5
解:
随堂练习
2.求下列各式:
解:
3.化简下列各式:
4
=- a-1 .
=xy.
解: (1)原式=(1-a)(a-1)-
4
3
=-(a-1)(a-1)-
4
3
=-(a-1)
4
1
(2)原式=[xy2(xy-1) ] (xy)
2
1
3
1
2
1
=(xy2x y- ) x y
3
1
2
1
2
1
2
1
2
1
=(x y ) x y
2
3
2
3
3
1
2
1
2
1
=x y x y
2
1
2
1
2
1
2
1
(3) (1-a)[(a-1)-2(-a) ] .
2
1
2
1
∴a-1<0.
(3)由(-a) 知 -a≥0,
2
1
∴原式=(1-a)(1-a)-1(-a)
4
1
=(-a) .
4
1
4.计算下列各式:
解:
5.比较
的大小.
解:
6.化简
解:
练习(第54页)
习题答案
